首先構造一個物理情境:一天體 m 在中心天體 M 的重力作用下由無窮遠處 勻速 運動至A點,重力方向與天體運動方向相同——均指向 M 。
要使 m 勻速 運動, m 上必然還有一個指向 右邊 的 外力 ,這個力要去和重力構成二力平衡,與重力等大反向。這一過程中,「 外力所做的功 」被物理學家 定義 為重力勢能!

E_{p}:=W_{外} (等號前加個冒號,是「被定義為」的意思。)
把 m 從無窮遠處拉至A的過程中, M 與 m 的間距不斷減小,萬有重力和外力不斷增大,是變力。處理 變力做功 問題,需要借助 積分 。
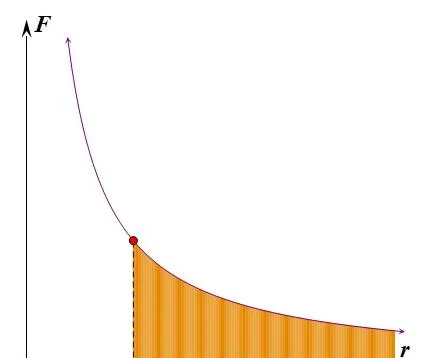
那麽,如何求 W_{外} ?功的定義式如下:
W=\vec F·\vec x=\left| \vec F \right|\left| \vec x \right|\cos<\vec F,\vec x> (尖括弧表示兩向量的夾角。)
先關註微元,再整體思考,可得
dW_{外}=\frac{GMm}{r^2}(-dr)\cos180°
W_{外}=\int_{\infty}^{r_{A}}\frac{GMm}{r^2}(-dr)(-1)
為什麽 \left| \vec x \right|=-dr 呢?根據定積分的定義,這裏 dr=\lim_{n \rightarrow \infty}{\frac{r_{A}-r_{\infty}}{n}} 。(無窮大不能直接介入計算,所以設 r_{\infty} 為一個很大很大、確定的 r 值。)很明顯 r_{A}\ll r_{\infty} , dr<0 。而 \left| \vec x \right| 是 向量的模長,必須大於零 。這就是 第二處負號的由來了 。

回到剛才的推導,
W_{外}=\int_{\infty}^{r_{A}}\frac{GMm}{r^2}dr
W_{外}=GMm\left[-\frac{1}{r}\right]_{\infty}^{r_{A}}\rightarrow GMm\left[(-\frac{1}{r_{A}})-(-0)\right]
W_{外}=-\frac{GMm}{r_{A}}
即 E_{P}=-\frac{GMm}{r_{A}}
由此可得,
兩天體相距 r 時, 以無窮遠處為零勢能點 ,重力勢能為: E_{p}=-\frac{GMm}{r} .









