一、同一物體的各個部份,速度可以不同
首先,需要向題主明確強調的是:對於同一物體,各部份的速度本身就可以不同。
其實,這是一個很明顯的常識。
物體只有在不發生自身轉動的情況下,各部份的速度(大小 和 方向)完全相同。譬如:做勻加速直線運動的小木塊、月球圍繞地球公轉,都屬於這種情況。
反之,如果物體本身發生轉動,那麽各部份的速度都不相同。否則,物體就無法實作轉動。 (劃重點)
一個最經典的例子就是:同一個圓盤上的兩個點,離轉軸越遠的點,旋轉半徑越大,從而線速度也越大。
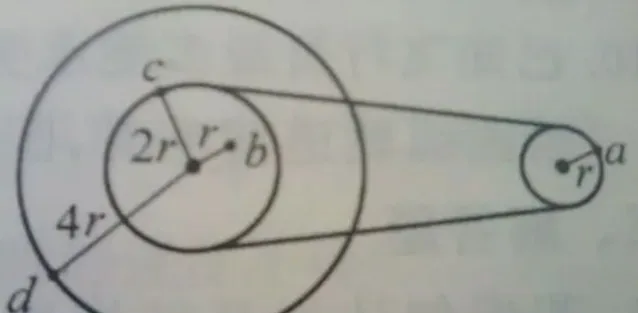
如圖所示,對左邊的大轉輪,由於 b、c、d 三點的轉動半徑依次增大,故這三個點的線速度大小也依次增大。對於曲線運動來說,線速度的定義就是運動弧長的瞬時變化率。其中,對勻速率圓周運動, 線速度等於單位時間內運動的弧長,即 v=\frac{2πr}{T} 。
再如:地球表面各個位置的自轉速度都不相同。其中:① 在同一條經線的不同位置,自轉速度的方向相同,但緯度越高,自轉速率越小。② 在同一條緯線中的不同位置,自轉速率相同,但自轉速度的方向不同。

二、以題主給出的模型為例
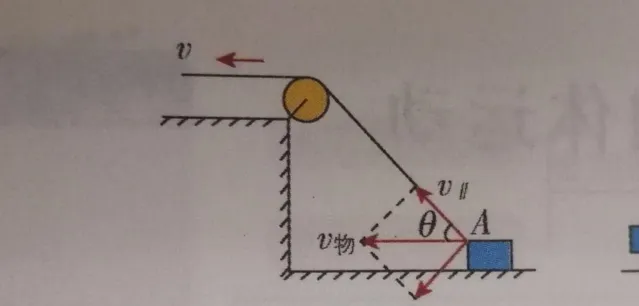
對於題主給出的這個「岸上人拉岸下物」模型來說,如果以地面為參考系,則:
① 整個運動過程中,這根繩子只有定滑輪左側水平的部份,繩上每個點的速度都等於人拉繩子的速度 v ;而定滑輪右側斜向下的部份始終圍繞定滑輪順時針轉動,故每個點的速度都不相同。其中,繩子物端(即 繩子與物塊相接的那個點)的速度剛好等於物體的速度 v_物 。
② 又由於整個運動過程中,繩子的長度保持不變(繩子始終處於繃緊狀態,既沒有松弛,也沒有斷掉),因此繩子各點沿繩子方向的分速度,其大小始終保持一致。對於這道題目,定滑輪左側水平的部份,沿繩子方向的速度,就是它自身的速度;定滑輪右側斜向下的部份,每個點沿繩子方向的速度,就是它沿繩子方向的分速度。
由 ①,可得 {\bf v}// {\bf v}_{物} 。即:繩子人端與繩子物端的速度方向始終保持平行。
由 ②,可得 v_{//}=v ,它起到使繩子各點依次沿定滑輪平動的運動效果,它只改變繩子每個點的路程,不改變繩子與水平面的夾角。對於任意時刻 t ,定滑輪左側繩子增加的長度 與 定滑輪右側斜向下減少的長度 始終保持相同,二者都等於 v_{//}\cdot t 。
v_{⊥} 起到使繩子繞定滑輪轉動的運動效果,它只改變繩子與水平面的夾角 θ ,不改變繩子每個點的路程。並且,任意時刻,離定滑輪越遠的位置, v_⊥ 越大。
由此可見,該題目本質上屬於「繩模型」的一種具體情景。因為整個過程只涉及繩子各部份速度之間的關系。這裏的「人」和「物體」僅僅用來直觀、形象地反映繩子兩端的速度。
聯立 ①②,我們可以求出在該過程中,任意時刻船速的大小為 v_物=v/ \cosθ ,繩子船端圍繞定滑輪轉動的分速度大小為 v_{⊥}=v \tan θ 。
在這個問題中,繩子人端的速度 v 為定值。隨著時間的推移, θ 逐漸增加, \cos θ 逐漸變小,於是繩子物端的速度 v_物 逐漸增加。故物體做水平向左的變加速直線運動。
三、一些初學者的常見誤區
對於「岸上人拉岸下物」模型,一些初學者可能會錯誤地認為繩子上各點的速度的方向都是沿繩的。於是就將繩子物端的速度也被認為是沿繩斜向左上方的 v ,然後將其分為水平向左和豎直向上的分速度。就像這樣:
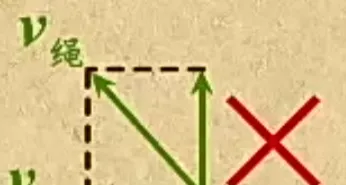
實際上,從圖中,我們可以很明顯地看出,整個運動過程中,繩子物端始終與物塊相接。物塊向左走了多少路程,繩子物端也向左走了多少路程。故繩子物端與物塊的速度始終是相同的。
另外,無論是運動學問題,還是力學問題,一定要先選擇參考系,要具體說明「以 XX 為參考系,……」。否則,就沒有任何物理意義。 (劃重點)
具體來說,「人端的繩速大小為 v_0 」是以地面為參考系得到的結論;而「船端的繩速大小為 v_0 」則是以某個隨繩轉動的參考系中得到的結論。但是,無論選擇哪個參考系,繩子上所有點的速度都不可能相同,否則繩子就無法繞定滑輪轉動。假如繩子船端相對於地面的速度就是沿繩斜向左上方的 v_0 ,則從人拉繩子的一開始,繩子的船端由於只沿繩收縮,但不圍繞定滑輪轉動,從而與船發生斷裂。 (劃重點)
————————————
我們在日常生活中經常接觸到的許多關於運動的表述,從物理學的層面,其實都犯了「沒有統一參考系」的錯誤。
譬如:我們日常講到的「月亮圍繞地球轉,地球圍繞太陽轉」這句話,從原則上就屬於不嚴謹、不規範的表述。
這是因為「月亮圍繞地球公轉」,是以地球為參考系得到的結論;而「地球圍繞太陽公轉」,又是以太陽為參考系得到的結論。——在物理學上,有一個預設的約定:如果沒有具體說明參考系,通常預設所有的物理量都是在同一個參考系下的結果。這是因為,只有統一參考系,才能保證系統內不同物件之間的物理量關系是確定且有意義的。
• 如果以地球為參考系進行運動學分析,根據相對運動的原理,可知:如果不考慮地球的自轉,月球和太陽都圍繞地球自西向東以橢圓軌域做曲線運動。其中,月球的公轉周期約為 27.32 天,太陽相對於地球的反向運動周期約為 365.25 天。從而,我們站在地球表面從天空中,可以看到太陽、月球都在天球上自西向東傾斜地做非勻速轉動,且月球的角速度約為太陽的 13.37 倍。

• 如果以太陽為參考系進行運動學分析,有:地球圍繞太陽自西向東以橢圓軌域做曲線運動,而月球圍繞太陽在地球公轉軌域附近做波浪線運動。——考慮到實際比例,月球的運動軌跡與地球公轉的軌域幾乎重合。其中,地球的公轉周期約為 365.25 天,月球在地球公轉軌域附近內外擺動的周期約為 27.32 天。

由此可見,透過選取不同的參考系,對太陽、地球、月球三者的運動進行描述,其運動軌跡也會大不相同。
四、桿模型
一根長直輕桿 AB 在墻角沿豎直墻和水平地面滑動。當桿 AB 與墻的夾角為 θ_{\rm A} ,與地面的夾角為 θ_{\rm B} 時,桿的 A 端沿墻下滑的速度大小為 v_{\rm A} ,桿的 B 端沿地面向右的速度大小為 v_{\rm B} 。則 v_{\rm A}:v_{\rm B} 等於多少?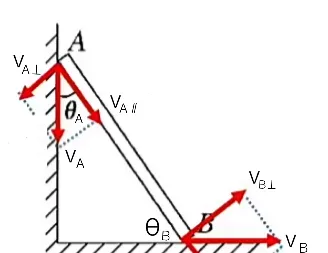
① 桿在滑動的過程中,A 端速度 v_{\rm A} 的方向始終沿墻豎直向下,B 端速度 v_{\rm B} 的方向始終沿地面水平向右。即 {\bf v}_{\rm A}⊥{\bf v}_{\rm B} 。
② 類似於題主給出的繩模型,在任意時刻,桿的長度保持不變,故桿上各點沿桿方向的分速度大小和方向始終保持一致。於是,對 A、B 兩端,滿足關聯等式 v_{\rm A //}=v_{\rm B//} 。
桿上各點垂直於桿方向的分速度共同使桿產生轉動的運動效果。其中,A 端垂直於桿的分速度 v_{\rm A ⊥} 使桿與地面的夾角 θ_{\rm B} 逐漸減小,B 端垂直於桿的分速度 v_{\rm B⊥} 使桿與墻面的夾角 θ_{\rm A} 逐漸增加。
聯立 ①② 可得, v_{\rm A //}= v_{\rm A} \cos{\rm θ_A}=v_{\rm A} \sin{\rm θ_B} , v_{\rm B //}= v_{\rm B} \sin{\rm θ_A} =v_{\rm B} \cos{\rm θ_B} 。
故 \frac{v_{\rm A}}{v_{\rm B}}=\tan {\rm θ_A}=\frac{1}{\tan{\rm θ_B}} 。
五、一定都要分解成沿桿和垂直於桿的分速度嗎?
用鉸鏈固定的桿子一端連一小球,最初球靠在可自由移動的木箱上。現讓箱子以速度 v_{木箱} 向右勻速運動,當桿子與豎直方向的夾角為 θ 時,小球的速度 v_{球} 是多少?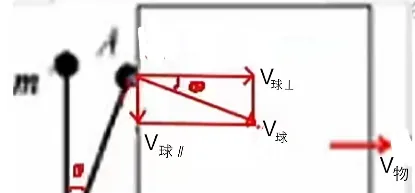
這個模型中,隨著木箱向右勻速運動,從而桿相對於鉸鏈(轉軸)順時針旋轉。其中,小球的速度 v_{球} 的方向始終垂直於桿向右,故小球並沒有完全沿桿方向的分速度,即 v_{球 ⊥}=v_球 ,v_{\rm 球 //}=0 。因此,這道題肯定無法利用桿上兩點之間的關聯加以求解。
故我們需要尋找小球與其他物體(或者其他物體上的點)之間的分速度關聯。
那麽,如何找到該模型中,兩點分速度之間的關聯呢?——它決定了我們應該將速度沿哪個方向進行分解。
由於整個過程中,小球始終靠在木箱上,故物體水平向右移動了多少位移,小球也水平向右移動了多少位移。於是,對於相互接觸的兩個物體之間,它們的垂直於接觸面的分速度相等。故我們應將小球的速度 v_{球} 分解成垂直於接觸面水平向右的分速度 v_{球 ⊥} 與沿接觸面豎直向下的分速度 v_{球//} 。[為保證符號的規範性,這裏仍然采用相同的分速度下標進行表示。]
對小球和木箱上的任意一點,均滿足關聯等式 v_{木箱}=v_{球⊥} 。
其中, v_{球⊥}=v_{球} \cos θ 。
故 v_球 = \frac{v_{木箱}}{\cos θ} 。
六、「關聯等式」小結
• 對於繩關聯模型,有繩子兩端沿繩方向的分速度大小相等。
• 對於桿關聯模型,有桿兩端沿桿方向的分速度相等。
• 對於接觸關聯模型,有兩物體垂直於接觸面(切面)的分速度相等。
• 繩關聯模型 與 桿關聯模型 中,繩子上任意一點垂直於繩的分速度 或者 桿上任意一點垂直於桿的分速度,都滿足線速度與角速度的換算公式 v_⊥ = ω \cdot r 。它起到繃緊的繩子或桿圍繞某個旋轉中心轉動的效果,從而使繩子或桿與水平面或豎直面的夾角發生變化。
高中階段涉及到的關聯速度分解題目,大多可以歸結為 以上三種基本模型的關聯等式 以及 線速度與角速度的換算公式 之間的組合。










