我從數學角度給一個標準答案吧: 有可能,並且這個可能性還不算太小。換個角度說,猴子贏下職業九段所需要花費的時間,即使只在「科學領域 」 ,都算不上一個特別大的數。
不得不說,日常生活限制了大部份人對數碼的想象。但即使是日常生活,都存在一些大得驚人的數,這些數都比猴子贏下職業九段的時間要長得多。
在這裏,我們定義一個新的單調遞增函數 g(x) 用於解釋科學領域大數的層級。它的範圍是 g(x)\in [0,3] ,也就是說,無論多大的數,我都可以對映到一個不超過 3 的數中。在這個對映關系下,「猴子贏下職業九段所需要花費的時間」對應的函數值大約在 1.01~1.02 之間。
第一層 (0,1]:粒子的計數
在這個函數下,生活中的絕大多數數碼,對應的值都不超過 1。
比如:
事實上,第一層的上限 g^{-1}(1)\sim10^{80} 。這個 10 的 80 次方, 大約就是 宇宙中粒子的總數 。
也許你想說:怎麽一上來就上核武器啊?
別著急,比起我接下來要講的數,我們才剛剛開始而已。
第二層 (1,2]:粒子的排列
事實上,「計數」是一種很原始的表達方式,即使把宇宙中所有粒子都算上,都可以用簡單的科學計數法搞定。
但是一旦涉及到「排列」問題,我們很容易得到一個比第一層大得多的數。其對應的增長速率,也會遠高於第一層中所熟悉的數。
魔術方塊大家都熟悉吧?一個最常見的三階魔術方塊,它的不同狀態數就有 4.33\times10^{19} 個;稍微大一點,五階魔術方塊,不同狀態數達到 2.83\times10^{74} 個,已經接近宇宙粒子總數的數量級了;而六階魔術方塊,不同狀態數高達 1.57 \times10^{116} ,遠超宇宙粒子總數。事實上,如果定義 m(x) 為 x 階魔術方塊的狀態總數,這個函數的增長是非常快的。當 x 不超過 15 時,m(x) 的值如下表所示:
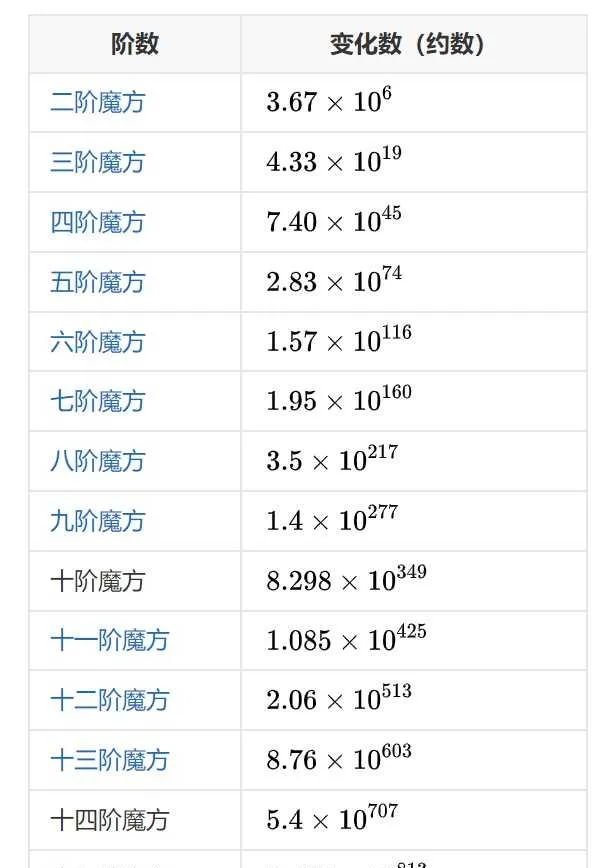
事實上,幾乎所有有一定復雜性的智力遊戲,其「狀態數」和「過程數」都在這一層。
就比如本問題中,猴子和人下棋:
上面只是非常粗略的估計, 根據這個估計,「猴子贏下職業九段需要花費的時間」大約會在 10^{600}\sim10^{800} 這個數量級。這個數對應的函數值是多少呢?大概是在 1.02~1.04 之間。
增補:這是一個非常非常松的上界,考慮到猴子只占其中一半的步數,而職業九段下棋的隨機性遠不如猴子那麽大,數量級還可以進一步降低接近一半,或許 10^{300}\sim10^{400} 就已經足夠,對應的函數值在 1.01~1.02 之間。因為,僅僅對 10^{80} 個粒子進行簡單排列,其不同的狀態數就有 10^{80}! 個,這個數看起來很大,但位數不超過 81\times 10^{80} 位,也就是說,這個數至多 10^{10^{82}} ,它其實也沒多大,但比 10 的 300~400 次方還是要大得多。
事實上,考慮到宇宙的空間很大,遠大於粒子本身所占據的空間,因此微觀狀態數還會更多一些,但也不會超過 10^{10^{120}}
因此,作為第二層的上限, g^{-1}(2)<10^{10^{120}} 。
順便提一句, 「猴子敲出莎士比亞全集」的時間也在這一層中,並且比「猴子贏下職業九段需要花費的時間」要長得多,但對應的函數值也不過在 1.05~1.08 之間(大概是 10 的幾十萬次方)。
第三層 (2,3]:粒子的回歸
比「粒子的排列」更大的數是什麽呢?是粒子的回歸。
展開地說,就是隨機運動的微觀粒子,是有機會回到原來位置的。如果一個區域中的所有粒子都幾乎回到了原來的位置,那麽其所需要花費的時間大約就在這一層級。
舉個通俗的例子:我們都知道「破鏡無法重圓」。但事實上,當我們把破鏡的所有碎片收集起來裝在一起,只要經歷足夠多的時間,它是可以重圓的,只是重圓所需要的時間,大概會在第三層,雖然這只是第三層入門。
而這個層級的上限,就是「龐加萊回歸時間」:在一個封閉系統中,任何粒子在經過一個漫長的時間之後必然能回到其無限接近其初始位置的位置(但是不能回到原來位置,只能無限接近),這樣一個周期就稱為一個龐加萊回歸。
龐加萊回歸時間有多大呢?有些 文章 會對它進行估算,比如算出太陽系的龐加萊回歸時間大約是 10^{10^{10^{76.66}}} ,如果使用 Linde's stochastic inflationary models 計算整個宇宙的龐加萊回歸時間,大約是 10^{10^{10^{10^{12.6}}}} 。
這才是「科學領域」中最大的有意義的數。比起這個數,猴子贏了職業九段根本不值一提。
--
在科學領域之外……
事實上, 在數學領域中,即使是宇宙中最大有意義的數 g^{-1}(3) ,依然是小得可憐的數。
在「大數學」( googology )中,人們定義了一套更加嚴謹的從序數到函數的對映系統,叫 f(x) 系統(fast-growing hierarchy,簡稱 FGH),詳細的定義可以參見 這裏。
「龐加萊回歸」時間的表示方式,也不過是最最基礎的「冪塔」而已,從數學上來說,它甚至小於 10\uparrow\uparrow5 (這不過是 2 層 高德納箭頭 而已!),在 FGH 中,我們也只能給到 2~3 的序數值。
它比起大數學中的入門「葛立恒數( Graham's number )」,還差了 2 層「人到神仙的距離」。
而比起目前人類目前承認的最大數「巨大數庭園數」 (Large Number Garden Number,簡稱 LNGN),它至少差了至少 10 層「人到神仙的距離」。
但即便是「巨大數庭園數」,依然和「無限」毫無關系。
警告:不要輕易使用 \infty ,這個數比你想象中的要大得多得多!
---
拓展閱讀:











