(本回答的目標讀者是線性代數的初學者。)
先回答題主的問題:
矩陣是對線性變換的表示;對於同一個線性變換,基選擇的不同,表示該線性變換的矩陣就不同。
接下來我試著解釋這句話。
由於我們研究的物件是『 線性變換 』,而不是『矩陣』,所以在繼續往下看之前, 建議暫時忘記一切關於『矩陣』的內容 ,直到我提到這個概念為止。
好,開始了呦。
一個線性變換是一個 函數 。一旦確定了函數對於定義域中每一個元素的作用,也就確定了這個函數。對於線性變換來說,我們需要知道 每一個向量 被變換到了哪裏。
由於這個變換是 線性 的,所以我們只需要知道 一組基向量 被變換到了哪裏,就可以知道任何一個向量的被變換到哪裏了。
什麽意思呢?我們具體一點來看:考慮一個線性變換T:V\rightarrow W ,我們想要知道V 中每一個向量v 去了哪裏,我們只需要知道V 的一組基向量v_{1},...,v_{n} 去了哪裏(因為V 中任意向量都是基向量的線性組合),也就是要知道T(v_{k}) 是W 中的哪一個向量。
那我們怎麽描述W 中的一個向量呢?同樣的道理,我們可以用W 的一組基向量w_{1},...,w_{m} 來描述W 中的任意一個向量。
這下就好辦了,為了表示一個線性變換T:V\rightarrow W ,我們選擇V 的一組基向量v_{1},...,v_{n} ,再選擇W 的一組基向量w_{1},...,w_{m} ,接著,把T(v_{k}) 用w_{k} 表示出來,就搞定了!
也就是說,我們把每一個T(v_{k}) 寫成w_{k} 的線性組合:
T({v_{k}})=a_{1,k}w_{1}+...+a_{m,k}w_{m}
再說一遍, 這個式子描述了V 的第k 個基向量被變換到W 中之後的位置。
所以,選定了V 與W 的基向量之後,線性變換可以由a_{j,k} 唯一確定,其中j=1,...,m ,對應的是W 的基,k=1,...,n ,對應的是V 的基。
好了,你肯定猜我要說:『我們把a_{j,k} 寫成m\times n 的矩陣中第j 行第k 列的元素。』
先不急,這句話是對的,但我要說的不是這個。來看一張圖:
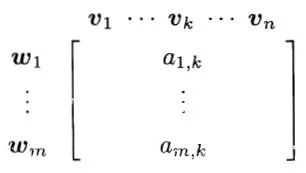
(這張圖的來源是【Linear Algebra Done Right】。)
這張圖描述的是我們如何透過選定的V 與W 的基向量來構造m\times n 的矩陣:
把定義域的基向量v_{1},...,v_{n} 寫在上方,把目標空間的基向量w_{1},...,w_{m} 寫在左側。
接著,按照之前所說的:
把每一個T(v_{k})
寫成基向量w_{i}
的線性組合,所需要的系數就構成了矩陣的第k
列。
把每一個T(v_{k})
寫成基向量
w_{i}
的線性組合,所需要的系數就構成了矩陣的第k
列。
把每一個T(v_{k})
寫成基向量
w_{i}
的線性組合,所需要的系數就構成了矩陣的第k
列。
最重要的話重復三遍。
再看一下圖,從矩陣M(T) 中我們又可以得到T(v_{k}) :將矩陣的第k 列的每個元素與左側相應的w_{j} 相乘,然後把所得向量相加,就得到了T(v_{k}) 。
以上這部份內容請反復看。
好的,給個例子。偷懶的我就用書上的例子了。
線性變換T:\mathbb{R}^{2} \rightarrow \mathbb{R}^{3} 定義為:
T(x,y)=(x+3y,2x+5y,7x+9y)
我們選擇標準基來描述——\mathbb{R}^{2} 的標準基是(1,0),(0,1) ,\mathbb{R}^{3} 的標準基是(1,0,0),(0,1,0),(0,0,1) :
我們想知道T 把\mathbb{R}^{2} 的標準基變換到了哪裏,於是代入上式:
T(1,0)=(1,2,7)=1(1,0,0)+2(0,1,0)+7(0,0,1)
T(0,1)=(3,5,9)=3(1,0,0)+5(0,1,0)+9(0,0,1)
於是,T 關於標準基的矩陣是:
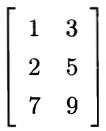
就是這樣。嗯。
現在再看『一個矩陣對應了一個線性變換』這個說法,就可以知道這個說法並不嚴謹。實際上, 只有確定了基向量之後,一個矩陣才對應一個線性變換 ;否則,只要換一組基,同一個矩陣對應的線性變換就不同了。
那為什麽我們經常還說『一個矩陣對應了一個線性變換』呢?因為一般來說,如果不明確指出,我們都預設使用標準基。
知道了上述內容,那麽矩陣乘法的意義也就很好理解了。
設v_{1},...,v_{n} 是V 的基,w_{1},...,w_{m} 是W 的基,u_{1},...,u_{p} 是U 的基。考慮線性對映S:U\rightarrow V 與T:V\rightarrow W ,分別對應矩陣M(S) 和M(T) 。
當我們定義了矩陣乘法之後,它們的復合對映TS:U\rightarrow W 就對應了M(TS)=M(T)M(S) 。具體的證明在教材上都會有,但我建議最好自己動手驗證一下。
但註意,這個優美的性質成立的前提是, 兩個矩陣必須選擇的是同一組V 的基v_{1},...,v_{n} ,否則不成立。當然,我們一般用的都是標準基,所以大多數時候不會有這個問題。
那如果出現基不一樣的情況,該怎麽辦呢?
答案是:我們可以用矩陣來換基啊!
我們再來看一下之前的圖:

矩陣本身的意義中就有『換基』,只是我們一般都用標準基,所以『換基』並沒有體現出來。
所以,我個人認為,有些教材上把換基矩陣區分為『無線性變換的換基矩陣』和『有線性變換的換基矩陣』實際上是多余的(但也許這樣是為了更直觀地描述分解操作),因為 每一個矩陣都是『線性變換+換基』 。
實際上 『無線性變換的換基矩陣』完全可以理解成『恒等變換+換基』 ,所以,空間的維數不變,m=n ,是正方形矩陣。
我們來看一下一些教材上對『無線性變換的換基矩陣』的定義:
如果v_{1},...,v_{n} 和v'_{1},...,v'_{n} 是V 的兩組基,對於\forall~ i,j \in \left\{ 1,...,n \right\} ,存在B_{i,j} \in \mathbb{R} ,使得v'_{j}=\sum_{i=1}^{n}{B_{i,j}v_{i}} 。我們把矩陣B=(B_{i,j}) 稱為『把v'_{i} 換成v_{i} 的換基矩陣』。
於是有人就不理解了,看v'_{j}=\sum_{i=1}^{n}{B_{i,j}v_{i}} 這個描述,這個矩陣B 明擺著是把v_{i} 變成了v'_{i} 呀,為什麽要反過來說呢?
其實並沒有反,正如我之前所說的,B 實際上是『恒等變換+換基』的矩陣,跟其他矩陣沒有什麽不同:I(v'_{j})=\sum_{i=1}^{n}{B_{i,j}v_{i}} ,這樣一來,再看一下之前的那張圖,v'_{i} 是寫在上方的,v_{i} 是寫在左側的。所以, 這個矩陣其實描述一個恒等變換,變換之前用的是一組基v'_{i} ,變換之後用的是另一組基v_{i} ;而由於恒等變換的效果看不出來,所以這個矩陣看起來就只是在換基。
這樣一來,『為什麽把非標準基換成標準基的矩陣就是把非標準基的向量豎著寫下來』也就一目了然了,因為每一個非標準基向量寫成標準基的線性組合,系數恰好就是該向量的對應位置的座標。(把這個想清楚對於理解矩陣很重要。)
而『把v'_{i} 換成v_{i} 的換基矩陣』與『把v_{i} 換成v'_{i} 的換基矩陣』這兩個矩陣是 互逆 的,這個很容易證明。( 證明它!! )
於是,對角化矩陣就很好理解了。
一個線性變換T 對於標準基(或者其他某個基)的矩陣為A ;而我們為了更清楚地透過矩陣看出這個線性變換的效果,就把A 對角化:
A=PDP^{-1} (D 為對角矩陣)
這其實就是先把標準基換成由特征向量組成的基(這是P^{-1} 的意義),於是每一個基向量在經過T 變換之後都只是乘了一個常數(這是D 的意義),最後再把由特征向量組成的基換回標準基(這是P 的意義)。
而剛剛說過,『把非標準基換成標準基的矩陣就是把非標準基的向量豎著寫下來』,所以(按照D 中特征值的順序)把對應的特征向量豎著寫下來,就得到了P 。
所以對角化其實就是要 用一組比標準基更好的基來描述線性變換 ,也就是 由特征向量組成的基 。
那有沒有比這個更好的基呢?有呀,就是 由特征向量組成的規範正交基 ,而這正是 譜定理 所研究的物件,這裏就不敘述了=w=
寫這個回答是因為我發現,很多時候別人問我問題,都是由於還沒有清晰地理解矩陣與線性變換之間的關系,而我覺得這應該是線代的基礎中的基礎。所以就把這些東西寫在這裏,希望對題主和其他人有所幫助,同時自己也再鞏固一遍。
那麽就寫到這裏。馬上去上課了!
這篇回答依然獻給那個正在學線代的小朋友=w=
那麽就這樣=w=











