以下有很多我個人的理解,相關內容詳見各類結構化學教材,推薦周公度先生的【結構化學基礎】和徐光憲先生的【物質結構】。
填充電子時,電子優先以能量較低的排布方式填入能階較低的軌域(構造原理),這裏面涉及的是空軌域的能量 \epsilon_{orbit} ;失去電子(電離)時,能量較高的電子優先失去,這裏涉及的是軌域中電子的能量 \epsilon_{electron} (電離能 I=-\epsilon_{electron} )。這是兩個不同的能量概念。當然,這裏提到的「空軌域的能量」和我們通常說的「軌域能」也不一樣,軌域能在數值上等於一個軌域中所有電子能量的均值。
徐光憲先生總結了兩個很簡練的經驗公式,用來判斷軌域或電子的相對能量高低:
填充電子時,空軌域的能量 E_{orbit}=n+0.7l ;失去電子時,電子的能量 E_{electron}=n+0.4l 。其中, n、l 分別是主量子數和角量子數。
那麽對於電離過程來說,顯然 E_{electron,3d}=3.8<E_{electron,4s}=4 ,所以4s電子總是優先失去。
所以這個題答案是 Fe\left([Ar]3d^64s^2\right) 。
為什麽會這樣呢?本質上還是取決於體系(原子核-電子)整體的能量變化,當然考慮到原子核質素數千倍於電子,其動能、勢能都可以視為不變,僅考慮電子能量即可(B-O近似)。
電子優先往哪一個軌域填充,取決於填充前後的能量差,能量降低越多者越優先;哪一個軌域的電子優先電離,取決於電離前後的能量差,電離所需能量越低者越優先。
總結一下就是,無論是填充還是電離,能使最終體系總能量最低者優先。原子核-電子體系的總能量不僅僅是電子軌域能量的總和,還要考慮電子間的相互作用,比如電子自旋成對能、電子互斥能等。
理論計算和光譜學數據表明,電子的有效半徑 \bar{r}_{3d}<\bar{r}_{4s} ,也就是3d電子離核更近,那麽3d電子受到K、L層電子的斥力就會更大,並且價電子間的斥力也有 J\left( d-d \right)>J\left( d-s \right)>J\left( s-s \right) ,而過渡金屬的成對能往往很小,可以忽略,這就導致電子填入3d軌域後的體系能量高於電子填充到4s軌域。按能量最低原理,電子會優先填入4s軌域。
對於電離而言,4s電子受到更多的內層電子的遮蔽,同時其有效半徑更大,受核吸引更弱,盡管 J\left( s-s \right)<J\left( d-d \right) ,剝離4s電子所需能量仍比剝離3d的更少,因此4s電子優先電離。
下面的表是電子結合能的實驗數據。電子結合能即軌域能階,數值上等於把原子特定(非空)軌域中的電子轟出來或向原子的特定(空)軌域放進一個電子時體系能量變化。
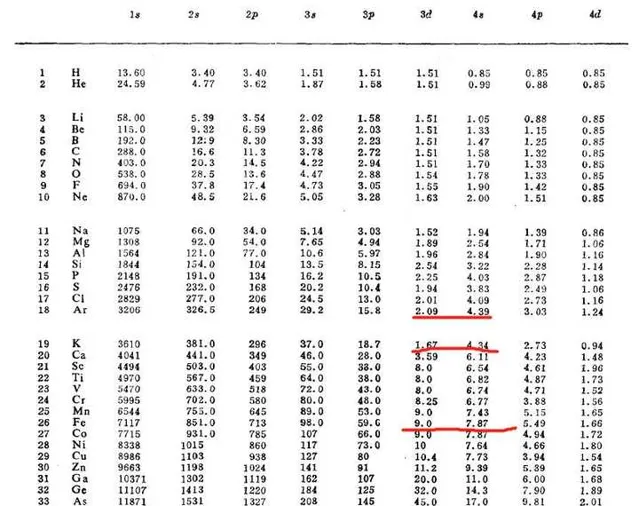
一眼可以看出,把 Fe,[Ar]3d^64s^2 的4s電子轟出來需要7.87 eV能量,轟出3d電子則需要9 eV,即4s電子能階更高,因此4s電子比3d電子更優先。
另一方面,對於電子填充時為什麽優先進入4s軌域,可以這麽看:當3s和3p填滿後( Ar^0 ),因為前面提到的電子-電子相互作用的影響,再向4s填充一個電子( Ar^-,[Ar]4s^1 )比向3d填進一個電子( Ar^-,[Ar]3d^1 )體系能量降低得更多( -4.39<-2.09\left( eV \right) )。考慮到 Ar^0 和 K^+ 的電子排布方式完全一致,僅核電荷數相差1,因此這可以說明電子會更優先向4s軌域填充。同時,對於3d軌域來說,從Ar到K、Ca,核電荷數增加,而電子卻填入了更外層的4s軌域,而4s電子對3d電子的遮蔽非常弱,因此在Ca之後, \epsilon_{3d} 出現了顯著的降低。
更深入的討論就要回到最初的起點了: i\hbar\frac{\partial}{\partial t}\Psi=\left( -\frac{\hbar^2}{2m}\nabla^2+V \right)\Psi=\hat H \Psi ,體系能量 E=\int_{}^{}\Psi^*\hat H\Psi d\boldsymbol \tau 。
並不打算就此展開,因為那些量子力學的推導我也很頭疼,但請容我放幾個公式裝裝逼:
進行一些適當的近似,比如忽略時間和原子核,對於單電子體系,比如氫原子,這個方程式可以展開為: \left( -\frac{\hbar^2}{2m}\nabla^2+\frac{e^2}{4\pi\epsilon_0r} \right)\psi\left( \boldsymbol r \right)=\hat H \psi\left( \boldsymbol r \right)=E\psi\left( \boldsymbol r \right) ,其中 \boldsymbol r=\left( x,y,z \right) 為位置向量, \psi 為定態波函數。
如果是n個電子的原子,稍微復雜一點: \hat H\psi(\boldsymbol r_1,\boldsymbol r_2...,\boldsymbol r_n)=E\psi(\boldsymbol r_1,\boldsymbol r_2...,\boldsymbol r_n) , \boldsymbol r_j=\left( x_j,y_j,z_j \right) 表示第j個電子的位置向量,且
\hat H=-\sum_{i=1}^{n}{\frac{\hbar^2}{2m_e}}\nabla_{\boldsymbol r_i}^2-\frac{1}{2}\sum_{j=1}^{n}{\frac{Ze^2}{\left| \boldsymbol r_j \right|}}+\frac{1}{2}\sum_{i=1}^{n}\sum_{j=1 \\ j\ne i}^{n}{\frac{e^2}{\left| \boldsymbol r_i-\boldsymbol r_j \right|}} ,三項分別表示電子動能、電子-核勢能和電子間靜電勢能。
計算化學裏會討論到含有n個電子、N個原子核的薛定諤方程式,可以簡單寫為: \hat H\psi(\boldsymbol R_1,\boldsymbol R_2...,\boldsymbol R_N;\boldsymbol r_1,\boldsymbol r_2...,\boldsymbol r_n)=E\psi(\boldsymbol R_1,\boldsymbol R_2...,\boldsymbol R_N;\boldsymbol r_1,\boldsymbol r_2...,\boldsymbol r_n) ,其中 \boldsymbol R_j=\left( X_j,Y_j,Z_j \right) 分別為第j個核的位置向量,並且
\hat H=-\sum_{i=1}^{N}{\frac{\hbar^2}{2M_i}}\nabla_{\boldsymbol R_i}^2+\frac{1}{2}\sum_{i=1}^{N}\sum_{j=1 \\ j\ne i}^{N}{\frac{Z_iZ_je^2}{\left| \boldsymbol R_i-\boldsymbol R_j \right|}}-\sum_{i=1}^{n}{\frac{\hbar^2}{2m_e}}\nabla_{\boldsymbol r_i}^2+\frac{1}{2}\sum_{i=1}^{n}\sum_{j=1\\ j\ne i}^{n}{\frac{e^2}{\left| \boldsymbol r_i-\boldsymbol r_j \right|}}-\frac{1}{2}\sum_{i=1}^{N}\sum_{j=1}^{n}{\frac{Z_ie^2}{\left| \boldsymbol R_i-\boldsymbol r_j \right|}} ,分別是核動能、核-核相互作用、電子動能、電子-電子相互作用以及核-電子相互作用。
啊!すばらしい!
以上。










