我不是學控制的，但是模擬電路是可以拿控制系統的那套理論來分析。之前有個哥們在我的專欄文章下面留言，說是我分析零極點的這套說辭實在是「清新脫俗」，可以跟學控制的同學分享一下。我可以講講一個電路裏面的零極點是怎麽回事。相信也可以讓你有些物理上的理解。
首先是極點。
我們來看張圖：
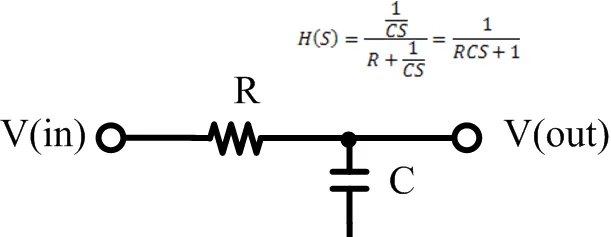一個R和一個C，便構成了一個最基本的極點。它的傳輸函數如圖所示，是1/（1+RCS）.因為s等於j\omega
，所以這裏的RC造成了一個左半平面的極點：-\frac{1}{RC}
。
等等！現實中怎麽會有負數的頻率呢？
所以，如果input signal裏面有這樣一個等於1/RC的頻率（如果是以Hz為單位，應該除以2\pi ）,那麽會發生什麽事情呢？
將\omega =1/RC 帶入上面的傳輸函數，這個傳輸函數的amplitude response就變成了\frac{1}{\sqrt{2} } .
哦！原來在bode圖裏，遇到一個極點就會有-3dB（20lg(1/\sqrt{2}) =-3dB ）的下降，跟這個確實可以對應起來呢！
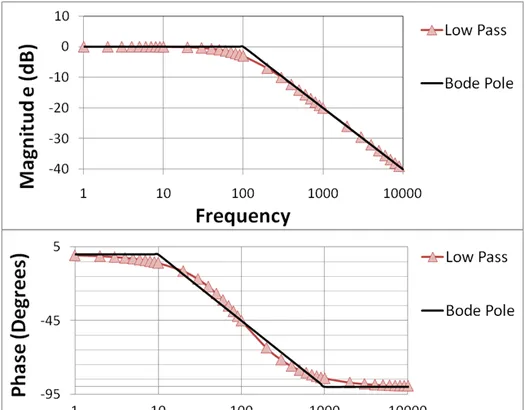
Source : Bode plot (Figure 1(b): The Bode plot for a first-order (one-pole)lowpass filter; the straight-line approximations are labeled "Bode pole"; phase is 90° lower than for Figure 1(a) because the phase contribution of the numerator is 0° at all frequencies.)
好吧！上面我們還是圍繞著傳輸函數的公式打轉，但是！但是為什麽會有恰好等於一半的amplitude response呢？
重新回到上面的圖。一個訊號經過一個R，會有一部份能量被R以熱能的方式散發出去。但是對於訊號本身的頻率、相位這些參數，R其實是沒什麽影響的。但是！但是還有一個C啊！這麽大一個電容連著output和gnd，你不能忽視人家嘛！
C和R不同的地方，在於它並不消耗能量，但是卻會改變相位。當input變化的時候，C上面的電壓也會跟著變化。這個不甘寂寞的C有個獨門秘技：「 吸和放 」！也就是說，當加在它上面的電壓忽然變化的時候，它會先吸走一部份，然後過一會再把被它吸走的電子重新放出來。
你見過月圓之夜時，清冷的月光灑在海面，深深的海底，巨蚌一張一合的樣子嗎？
那個，嘿嘿，不好意思啊，作者君也沒見過……不過看小說看過……
好了，不插科打諢了。總之，C就是個這麽神經兮兮的家夥。它明明不要你的電子，但是就是不情不願的要阻攔一下你的訊號，過一會兒再放一部份電子出來。
因為這個討厭的家夥，你的訊號被攔腰劫走了一部份。
H(S)=\frac{1}{1+j} =\frac{1}{\sqrt{2} } e^{-j\frac{\pi }{4} }寫成這樣，我們可以看出來，若是輸入訊號的頻率恰好等於\frac{1}{RC} ，那麽傳輸函數變成為了上面那個樣子。 增益變成了\frac{1}{\sqrt{2} } ，相位下降了45° 。
為什麽是45°呢？因為C這個家夥是故意等了90°之後才不情願的放出了你的訊號。因為一部份（當\omega =\frac{1}{RC} 的時候，恰好是一半）逃出C的魔掌的訊號沒有相位的延遲，而另外一部份不那麽幸運的訊號就被C戲弄了一番之後放了出來。所以最後在output看到的總的效果就是延時了45°。嗯，不是90°，也不是0°，就是一半，45°呢！
所以，若是想讓我們的訊號特別厲害，不受到這個討厭的C的毒害，我們的訊號應該變成什麽樣呢？讓我想想……那就是傳輸函數不就是1了嗎！那個時候，我們的訊號就別含變化量，直接是個DC的值，那麽只對變化量感興趣的C就懶得理你了！
還有，什麽時候我們的訊號被侵蝕得特別厲害，比如完全沒有了？再讓我想想……那就是大部份，或者說是幾乎全部的訊號都要先被C吸走再放出來吧？如果現在有個特別特別高頻的訊號，C就變得特別興奮了。對於高頻的訊號，C的內力變強，傳輸函數包含s的那項遠大於後面那個1，因而傳輸函數就變得無限趨近於零了。
嗯，好像input訊號的具體頻率其實起到了這樣一個效果： 它決定了是從R直接到output的訊號分量多呢？還是被C戲弄的訊號分量多。
話說，R和C的具體值也是很有意義的吧？
那當然了。作者君每次都 朝著極端的情況想 ：
比如，若是我沒有這個R，就一個孤零零的C，結果會怎樣？那就是input直接和output短接在一起了吧？那還擔心C幹嘛？
H(S)=\frac{1}{1+RCS} \simeq 1或者，若是R無限大，又會怎樣呢？額，訊號花了九牛二虎之力，才勉勉強強的穿過R的重重包圍到了output這邊。結果前有狼後有虎，剛過來便又遇到一個虎視眈眈的C在output這裏。唉！還是直接投降，任人魚肉算了！C要戲弄就讓它戲弄好了……
H(S)=\frac{1}{1+RCS} \simeq \frac{1}{RCS}= \frac{1}{RCj\omega }\rightarrow 0所以，1/RC的值和訊號頻率的相對位置，才是關鍵之處啊！若是RC超級小（比如很小的C只對更高的頻率感興趣。對於一些kHz什麽的小嘍啰，人家根本不care），我們的訊號還是很安全的。但若是RC超級大，比如有個巨無霸的C，就是那種巨大的巨蚌啦！人家什麽都喜歡，來者不拒，你的kHz的訊號也是它的愛好之一，那麽你就慘慘慘了……
或者還有一種方式理解極點：
之所以會有極點，就是因為當frequency上升之後，電容冒了出來，「一吸一放」。 或者可以這樣說，這家夥是開黑店的。有事沒事，路過的signal都被揪進去打了一頓才被放出來。（如果是DC，它不太敏感，也就放行了……）
其實你也 可以把pole理解成為兩個current source （中間是virtual ground，或者說，是真的ground）， 一個專門打家劫舍，搶signal；一個只做好事，放他哥們搶的signal出去。他們的電流都等於C*dV/dt。
所以在pole的frequency時，專門幹壞事個那家夥搶了一半的signal進了它的老巢。然後它那個只做好事的哥們過了90°又把人放了出來。
等到frequency很高的時候，打劫的那家夥就把所有的signal都搶了……然後它哥們還是繼續當老好人，過了90°又把人放了出來……實在是神經病的組合……
至於零點。在電路中，零點就是一條前饋通路。訊號不老老實實的按照你給它規定的路線跑，它找到了一條捷徑，抄近路了……比如你跟人一起去跑馬拉松，結果明明應該跑個圈再回來的，另外那哥們直接走了小路，省了幾十公裏的路……
首先是零點的基本分析：
說完了極點，我們再來看看它的對立面——零點。沒有對手的絕世高手註定是不存在的，因為世間萬物，必定有其相生相克的另外一個……哈哈！就此打住，否則作者君要開始描述一副「決戰紫禁之巔」的畫面了……^_^
我們還是拿一個最基本的電路模型來入手。
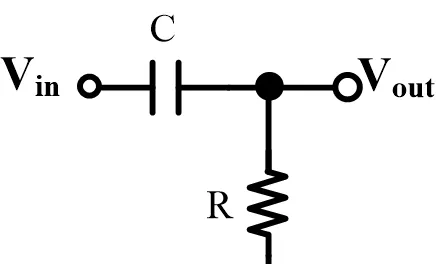
和前面計算極點的電路相反，這次電容C橫跨在了input和output之間，而output一段則有一個到地的R。非常自然的寫出transfer function：
H(s)=\frac{R }{R+\frac{1}{CS}} =\frac{RCS}{1+RCS} =\frac{RCj\omega }{1+RCj\omega }還是從頻率為無窮小開始看：這個時候分子無限趨於0，而分母無限趨於1,。因此，transfer function的amplitude就約等於0。如果單位換成了20dB的話，則是一個無窮小的數。
然後我們再來看看當頻率很大的時候：分母的那一項「1」可以忽略不計了。因此這個transfer function的amplitude就約等於1。單位換成20dB之後，就差不多是0了。
如果恰好\omega _{z} =\frac{1}{RC} ，那麽這個頻率就是我們所關心的零點頻率了。同之前的極點頻率類似，在這個零點頻率處，amplitude變成了1/\sqrt{2} ，phase變成了45°。
等等！為什麽書上都說，極點之後的amplitude以-20dB/dec下降，而零點之後的amplitude以20dB/dec上升呢？
前一篇我們仔細算了算，知道了極點下降的原因。那麽零點上升也就是差不多的道理了啦！
重新寫一下transfer function：
H(s)=\frac{RCj\omega}{1+RCj\omega}\approx RCj\omega上面這樣等效的成立條件，是頻率比較小的時候。因此，不知道大家發現了沒有，當分子的頻率j\omega 成為了整個transfer function的關鍵所在之時，20dB/dec上升其實也就成了自然而然的結果。
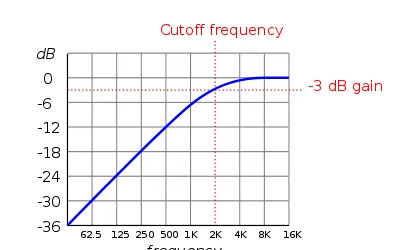
source:http:// manual.audacityteam.org /man/high_pass_filter.html
回憶一下推導極點時所用的bode plot：
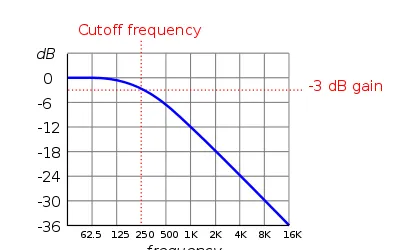
不知道大家註意到沒有：
開始在頻率小的時候，極點是沒什麽作用的；當頻率超過了極點頻率，則極點的作用就開始顯現出來了；
而零點則是頻率低的時候有影響，等到了高頻，則它的影響就忽略不計了。
是不是感覺有些玄妙？嗯，其實呢，說白了，就是j\omega 這項到底什麽時候冒出來。比如零點是當頻率低的時候，j\omega 在分子出現。所以呢，就有了20dB/dec的上升。
而對於極點來說，
H(s)=\frac{1}{1+RCj\omega } 只能是在頻率大，導致j\omega 那項遠大於1的時候，才能起到決定性作用。而且又由於它在分母的位置，所以才會最後導致高頻時的20dB/dec的下降。
再回去想想……哎呦！最上面那張圖不是電容跨在input和output之間嘛！高頻的時候，電容就相當於一根導線，那它自然也就不起作用了嘛！嗯嗯，好像就是這樣的！
然後是模擬電路裏面的零點：
我們來看看電路中基本的零點長得啥樣。
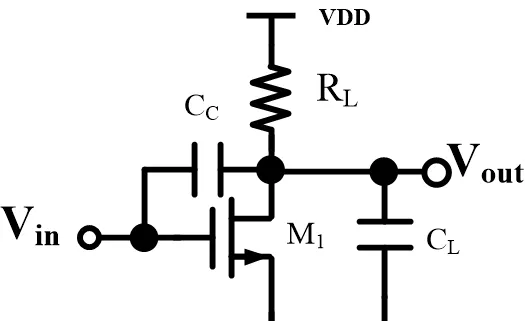還是一個簡單的單極點電路。和之前唯一不同的地方，在於gate和drain之間被加上了一個Cc。因為這個Cc的存在，這個電路中出現了一個比較明顯的零點。當然，一般的mosfet的Cgd都是不太大的，除非用在諸如兩級運放之間的miller capacitor那種Cc，這個零點才是我們需要考慮的。
傳輸函數：
H(s)=\frac{g_{m} R_o+RC_cS}{1+R_o(C_c+C_s)s}分母有個很明顯的極點，分子有個明顯的零點。極點咱們就先不管了，來看看這個零點：
\omega _z=-\frac{g_m}{C_c}很顯然，自然界沒有負數的頻率。因此，我們還是來關心\omega _z=\frac{g_m}{C_c} 好了。
Cc就相當於前一篇文章中提到的跨在input和output之間的電容，而gm從分子挪到分母去，則是之前的output接地電阻變成了1/gm。
話說，為什麽這個零點只跟這個nmos的gm有關系呢？
原因還是在於零點的特性：當頻率大於零點之後，這個零點才能逐漸被忽略掉。
設想一下，如果現在有個很高頻的input signal，那麽這個電路中唯一的nmos就變成了gate和drain短接在一起的一個diode了。一個diode的等效電阻是1/gm，所以這個零點也就跟gm有關了。
很多書上說， 零點的存在，其實是提供了一條所謂的「feed-forward」前饋通路。道理同上，也就是走了「捷徑」。捷徑的存在，導致本來應該被mos放大的signal直接跑到了output那端，自然也就嚴重的影響了mos的放大效能。
詳細內容可以參考我的專欄文章：
極點的物理意義：
知乎專欄單極點電路：
知乎專欄零點的分析：
知乎專欄零點的物理意義：
知乎專欄
