这篇回答节选自我的专栏 【机器学习中的数学:概率图与随机过程】 ,我们来仔细介绍和分析一下粒子滤波。
也欢迎关注我的知乎账号 @石溪 ,将持续发布机器学习数学基础及算法应用等方面的精彩内容。
我们知道,卡尔曼滤波是可以得到解析解的,而原因是 z_t 和 z_{t-1} 之间是线性关系,且变量服从高斯分布。我们回想一下,正式因为高斯分布的完美特性,导致了我们可以拿出滤波结果的解析解。
但是这毕竟是一种非常特殊的情况,换句话说,如果在更一般的情况下 z_t 和 z_{t-1} 之间不满足线性关系,而是可以满足任意关系,且变量不服从高斯分布,那么会是什么样的一种情形?这就是我们这里要介绍的粒子滤波。
粒子滤波中,我们同样最关系的也是滤波问题(filtering):即关注 p(z_t|x_1,x_2,...,x_t) 的概率分布,我们回忆一下分两步:
第一步: predict 。从贝叶斯的角度来说,实际上就是利用上一步 t-1 步的滤波值,先估计出一个 z_t 的先验概率:
p(z_t|x_1,...,x_{t-1})=\int_{z_{t-1}}p(z_t|z_{t-1})p(z_{t-1}|x_1,...,x_{t-1})dz_{t-1}
第二步: update 。在拿到 t 时刻的观测变量 x_t ,我们称之为证据之后,对上一步得到的 z_t 先验概率分布进行修正,得到我们要的滤波,本质上就是去求得 z_t 的后验分布:
p(z_t|x_1,...,x_t)\propto p(x_t|z_t)p(z_t|x_1,...,x_{t-1})
此时的我们,无法拥有高斯分布和线性关系这么完美的假设,因此不再能够像卡尔曼滤波那样得到滤波的解析解,怎么办?我们想到了之前学习过的蒙特卡洛方法,得不到解析解,我们去求数值解。
具体怎么弄,我们看一下重要性采样方法:
这里我们要树立一个观点,我们在 predict 和 update 两步的不断迭代过程中,都是在想着不断的求得 z 的概率分布,实际上分布并不是我们最终需要的结果,有了分布后,我们最终还要做一步就是,取分布中最大概率密度的那个 z 值作为我们的估计。
因此,数值解的方法,就是直接面向最终的估计值,如果说 z_t 服从概率分布 p(z_t|x_1,...,x_t) ,那么数值解方法的最终目标就是求得变量 z_t 的期望,来作为 t 时刻这一步滤波的估计值。那么每一步同样都能获得滤波结果。
具体怎么做,首先第一个要用到的思想就是重要性采样方法:
假如变量 z 服从分布 p(z) ,如何求得 z 的期望?
按照连续型随机变量期望的定义: E[z]=\int zp(z)dz ,进一步如果依据大数定理,依据采样的方法从分布 p(z) 中采出 N 个样本 z_i ,求他们的算术平均,同样可以作为期望的近似,这个我们在概率统计基础中已经多次讲过:
E[z]=\int zp(z)dz \approx \frac{1}{N}\sum_{i=1}^Nz^{(i)}
其中, z^{(i)} 就是从分布 p(z) 中采样出来的 N 个样本,但是问题来了,如何从 p(z) 中生成样本 z^{(i)} ,这个我们并不知道啊,换句话说 p(z) 是一个复杂的分布,我们没办法从中采到服从分布的样本。
重要性采样就呼之欲出了,他在求期望的过程中引入了一个建议分布 q(z) ,这个建议分布可以是一个任意的我们熟悉的分布,他可以使得我们可以轻松的从 q(z) 中生成服从 q(z) 分布的一系列样本。
那这个建议分布 q(z) 有啥用呢?还是回到期望的定义式中:
E[z]=\int zp(z)dz=\int z\frac{p(z)}{q(z)}q(z)dz
经过这么一个漂亮的变形,我们发现,随机变量 z 的期望就可以变成下面这种形式:
E[z]=\int z\frac{p(z)}{q(z)}q(z)dz \approx \frac{1}{N}\sum_{i=1}^Nz^{(i)}\frac{p(z^{(i)})}{q(z^{(i)})}
这时,这一组 N 个生成的样本 z^{(i)} 就不再是从分布$p(z)$中生成的了,而是从 q(z) 中生成的, q(z) 是我们指定的建议分布,因此用它来生成一组样本,我们还是办得到的
这个过程中 \frac{p(z^{(i)})}{q(z^{(i)}} 就称为样本 z^{(i)} 的权重,记作 w^{(i)} ,既有:
E[z] \approx \frac{1}{N}\sum_{i=1}^Nz^{(i)}\frac{p(z^{(i)})}{q(z^{(i)})}=\frac{1}{N}\sum_{i=1}^Nz^{(i)} w^{(i)}
好,回到粒子滤波的问题中来,我们的问题也是类似的:
在 t 时刻,我们用数值解求滤波的近似结果,实际上就是求服从分布 p(z_t|x_{1:t}) 的变量 z 的期望。那么套用重要性采样方法,我们引入建议分布 q(z_t|x_{1:t}) ,那么每一轮过程中,比如在 t 时刻:
我们用建议分布 q(z_t|x_{1:t}) 生成 N 个样本:
z_t^{(1)},z_t^{(2)},z_t^{(3)},...,z_t^{(N)}
然后再用权重公式公式 w_t^{(i)}=\frac{p(z_t^{(i)}|x_{1:t})}{q(z_t^{(i)}|x_{1:t})}
来对应的生成样本 z_t^{(1)},z_t^{(2)},z_t^{(3)},...,z_t^{(N)} 所对应权重 w_t^{(1)},w_t^{(2)},w_t^{(3)},...,w_t^{(N)} ,然后通过 \frac{1}{N}\sum_{i=1}^Nz^{(i)} w^{(i)} 来求得这一轮滤波值的期望。
但是问题来了,不像单纯的重要性采样中的情形,在上面的重要性采样的例子当中,我们虽然不能从 p(z) 中生成样本,但是毕竟我们知道 p(z) 的解析式,可以求得 p(z) 的值,但是粒子滤波中的时间 t 中, p(z_t^{(i)}|x_{1:t}) 我们也求不出来,只有当 t=1 时, p(z_1^{(i)}|x_1) 可以通过 p(z_1^{(i)}|x_1) \propto p(z_1^{(i)})p(x_1|z_1^{(i)}) 获得,
到了这儿,思路就明确了,怎么求?用递推,每一轮我们都的采样 N 个样本 z
那么在 t-1 时刻, N 个样本 z_{t-1}^{(1)},z_{t-1}^{(2)},z_{t-1}^{(3)},...,z_{t-1}^{(N)} 所对应的权重为 w_{t-1}^{(1)},w_{t-1}^{(2)},w_{t-1}^{(3)},...,w_{t-1}^{(N)}
而在 t 时刻 N 个样本 z_{t}^{(1)},z_{t}^{(2)},z_{t}^{(3)},...,z_{t}^{(N)} 所对应的权重为 w_{t}^{(1)},w_{t}^{(2)},w_{t}^{(3)},...,w_{t}^{(N)}
那么我们只要试图去求得两个对应位置上的样本 z_{t-1}^{(i)} 和$z_{t}^{(i)}$他们二者权重之间的递推关系,也就是 w_{t-1}^{(i)} 和 w_{t}^{(i)} ,从 t=1 开始,一步一步的采样 z_t^{(i)} ,一轮一轮的迭代出 w_{t}^{(i)} ,就能成功的实现滤波的目标。
下面我们来看具体如何求解
这里为了简化计算,用得是 p(z_{1:t}|x_{1:t}) 这个概率,这是一种简化运算的假设,大家注意这点就好,那么权重的表达式就表示为:w_t=\frac{p(z_{1:t}|x_{1:t})}{q(z_{1:t}|x_{1:t})}
我们看看如何化简这个表达式,首先看分子
p(z_{1:t}|x_{1:t})=\frac{p(z_{1:t},x_{1:t})}{p(x_{1:t})}=\frac{1}{C}p(z_{1:t},x_{1:t})
这里是因为 p(x_{1:t}) 是观测变量 x_{1:t} 的概率,很显然可以记作常数 C ,接着
p(z_{1:t}|x_{1:t})=\frac{1}{C}p(z_{1:t},x_{1:t})=\frac{1}{C}p(x_t|z_{1:t},x_{1:t-1})p(z_{1:t},x_{1:t-1})\\=\frac{1}{C}p(x_t|z_{1:t},x_{1:t-1})p(z_t|z_{1:t-1},x_{1:t-1})p(z_{1:t-1},x_{1:t-1})\\=\frac{1}{C}p(x_t|z_{1:t},x_{1:t-1})p(z_t|z_{1:t-1},x_{1:t-1})p(z_{1:t-1}|x_{1:t-1})p(x_{1:t-1})
这里由观测独立性假设有: p(x_t|z_{1:t},x_{1:t-1})=p(x_t|z_t)
由齐次马尔科夫假设有: p(z_t|z_{1:t-1},x_{1:t-1})=p(z_t|z_{t-1})
同时, p(x_{1:t-1}) 也是一组观测变量的概率,记作常数 D 。
最终化简为:
p(z_{1:t}|x_{1:t})=\frac{D}{C}p(x_t|z_t)p(z_t|z_{t-1})p(z_{1:t-1}|x_{1:t-1})
再看看分母 q 分布该如何化简,先按条件概率公式转化一下,
q(z_{1:t}|x_{1:t})=q(z_t|z_{1:t-1},x_{1:t})q(z_{1:t-1}|x_{1:t})
然后这里有一个小技巧,那就是时刻 t 以前的隐含变量的取值显然不受 t 时刻观测变量 x_t 取值的影响,因此就有:
q(z_{1:t-1}|x_{1:t})=q(z_{1:t-1}|x_{1:t-1})
那么:
q(z_{1:t}|x_{1:t})=q(z_t|z_{1:t-1},x_{1:t})q(z_{1:t-1}|x_{1:t-1})
那么此时我们权重 w_t 的表达式就能够完整的写出来了:
w_t=\frac{p(z_{1:t}|x_{1:t})}{q(z_{1:t}|x_{1:t})}\propto \frac{p(x_t|z_t)p(z_t|z_{t-1})p(z_{1:t-1}|x_{1:t-1})}{q(z_t|z_{1:t-1},x_{1:t})q(z_{1:t-1}|x_{1:t-1})}
我们欣喜的发现,等式的最后一部分就是 w_{t-1} 的表达式: \frac{p(z_{1:t-1}|x_{1:t-1})}{q(z_{1:t-1}|x_{1:t-1})}=w_{t-1}
w_t\propto \frac{p(x_t|z_t)p(z_t|z_{t-1})}{q(z_t|z_{1:t-1},x_{1:t})}w_{t-1}
而此时我们还需要补充一点的就是,由于 q 分布是我们的提议分布,意味着我们可以选择任意我们觉得方便的分布,那么我们让分布 q 取如下形式:
q(z_t|z_{1:t-1},x_{1:t})=p(z_t|z_{t-1})
最后一步转化是因为齐次马尔科夫性质决定的,那么 w_t 的递推关系就瞬间简单了:
w_t\propto \frac{p(x_t|z_t)p(z_t|z_{t-1})}{q(z_t|z_{1:t-1},x_{1:t})}w_{t-1}=\frac{p(x_t|z_t)p(z_t|z_{t-1})}{p(z_t|z_{t-1})}w_{t-1}=p(x_t |z_t)w_{t-1}
\Rightarrow w_t\propto p(x_t |z_t)w_{t-1}
而由于我们所有粒子 z^{(i)} 所对应的权重 w_t^{(i)} 最终要通过归一化处理使得他们的和为 1 ,因此这里的正比可以直接处理为相等,反正最终还要归一化的嘛:
\Rightarrow w_t=p(x_t|z_t)w_{t-1}
而我们发现 p(x_t|z_t) 反映的是 t 时刻隐变量 z_t 到观测变量 x_t 之间的转移概率,这个是模型已知的,由此 t 时刻和 t-1 时刻的权重递推关系就出来了。
有了这个递推关系,具体应该如何进行滤波的过程,我们在下一讲中详细介绍。
在上一讲中,我们已经得到了 t-1 时刻和 t 时刻权重之间的关系: w_t= p(x_t|z_t)w_{t-1} ,那么粒子滤波中的采样过程具体就描述如下,显然这是一个迭代的过程:
前提:在 t-1 时刻采样过程已完成
那么在 t 时刻,我们采样 N 个 z_t^{(i)} 个样本点
for \,\,\,i=1,2,...,N:
\,\,\,\,\,\, z_t^{(i)}\sim q(z_t|z_{t-1}^{(i)},x_{1:t})
\,\,\,\,\,\, w_t^{(t)}= w_{t-1}^{(i)}\frac{p(x_t|z_t^{(i)})p(z_t^{(i)}|z_{t-1}^{(i)})}{q(z_t^{(i)}|z_{t-1}^{(i)},x_{1:t})}
end:\,\,w_t^{(i)} 进行归一化,使得 \sum_1^{N}w_t^{(i)}=1
由于我们选择了提议分布 q : q(z_t^{(i)}|z_{t-1}^{(i)},x_{1:t})=p(z_t^{(i)}|z_{t-1}^{(i)}) ,则这个采样和权值迭代的过程就进一步简化为了:
for \,\,\,i=1,2,...,N:
\,\,\,\,\,\, z_t^{(i)}\sim p(z_t|z_{t-1}^{(i)})
\,\,\,\,\,\, w_t^{(t)}= w_{t-1}^{(i)}p(x_t|z_t^{(i)})
end:\,\,w_t^{(i)} 进行归一化,使得 \sum_1^{N}w_t^{(i)}=1
我简要的解读一下这个过程,实际上在时间 t 时刻,我们需要从分布 p(z_t|z_{t-1}^{(i)}) 中采样 N 个样本 z_t^{(i)} ,同时我们在上一步 t-1 时刻曾经也得到了一轮采样样本 z_{t-1}^{(1)},z_{t-1}^{(2)},z_{t-1}^{(3)},...,z_{t-1}^{(N)} ,其中每一个采样样本 z_{t-1}^{(i)} 对应的权重就是 w_{t-1}^{(i)} 。那么在时刻 t 的这一轮采样过程中,我们对于每一个采样样本 z_t^{(i)} ,仅仅通过 w_{t-1}^{(i)}p(x_t|z_t^{(i)}) 的迭代计算,我们就能获得该样本点 z_{t}^{(i)} 的权重 w_t^{(i)} 。
那么每一轮的权重都可以通过这种方法获得,至于说初始时刻的 w_1^{(i)} 如何获取,
当 t=1 时,带入有 w_1^{(t)}= w_{0}^{(i)}p(x_1|z_1^{(i)}) ,由于并没有 t=0 时刻,因此所有的 0 时刻权重 w_0^{(i)} 都处理为 1 。同时 t=1 时, z_t^{(i)}\sim p(z_t|z_{t-1}^{(i)}) 中的 p(z_t|z_{t-1}^{(i)}) 也直接就是初始概率分布 p(z_1)
那么我们把 t=1 时刻的情况带入,合并成完整的粒子滤波流程:
t=1:
for \,\,\,i=1,2,...,N:
\,\,\,\,\,\, z_1^{(i)}\sim p(z_1)
\,\,\,\,\,\, w_1^{(t)}= p(x_1|z_1^{(i)})
w_1^{(i)} 进行归一化,使得 \sum_1^{N}w_1^{(i)}=1
t\ge 2: 开始循环
for \,\,\,i=1,2,...,N:
\,\,\,\,\,\, z_t^{(i)}\sim p(z_t|z_{t-1}^{(i)})
\,\,\,\,\,\, w_t^{(t)}= w_{t-1}^{(i)}p(x_t|z_t^{(i)})
end:\,\,w_t^{(i)} 进行归一化,使得 \sum_1^{N}w_t^{(i)}=1
这里有一个点需要提醒一下大家:
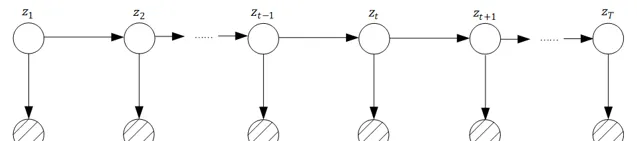
初始概率 p(z_1) ,状态转移概率 p(z_t|z_{t-1}) 和发射概率$p(x_t|z_t)$,这三种概率在隐马尔可夫模型、卡尔曼滤波和粒子滤波中都有,但是他们的表现形式不同,我们总结回顾一下:
对于隐马尔可夫模型,初始概率 p(z_1) 取自于概率向量 \pi ,而状态转移概率 p(z_t|z_{t-1}) 和发射概率 p(x_t|z_t) 取自于状态转移概率矩阵 A 和发射概率矩阵 B 中的对应项
对于卡尔曼滤波,三个概率都必须服从高斯分布: p(z_t|z_{t-1})=N(Az_{t-1}+B,Q) 和 p(x_t|z_t)=N(Cz_t+D,R),p(z_1)=N(\mu_1,\sigma_1)
而粒子滤波则没有任何约束,三个概率都可定义为任意函数形式:
p(z_t|z_{t-1})=f(z_{t-1}) 、 p(x_t|z_t)=g(x_t),p(z_1)=f_0(z_1)
那么我们从比较卡尔曼滤波和粒子滤波的角度来看看,从时间 t-1 时刻到 t 时刻的迭代本质到底是什么,先看看卡尔曼滤波,卡尔曼滤波关于隐变量 z_t 的估计,实际上是一个高斯分布:
我们知道,在 t-1 时刻,我们通过 predict 步骤,得到了一个预测概率
p(z_t|x_1,x_2,x_3,...,x_{t-1})\\=\int_{z_{t-1}}p(z_t|z_{t-1})p(z_{t-1}|x_1,x_2,x_3,...,x_{t-1})dz_{t-1}
这本质上是先拿到了隐变量 z_t 的一个先验高斯分布,然后我们在 t 时刻的 update 步骤,是我们观察到 t 时刻的观测变量 x_t ,对先验高斯分布进行修正,得到后验分布,也就是滤波的结果:
p(z_t|x_1,x_2,x_3,...,x_t)\propto p(x_t|z_t)p(z_t|x_1,x_2,x_3,...,x_{t-1})
简单点说,从 t-1 时刻的 predict 步骤到 t 时刻的 update 步骤,就是从一个高斯分布变化到另一个高斯分布的过程,高斯分布仅由均值和方差决定,因此前后需要发生改变的就是均值和方差,如下图所示:
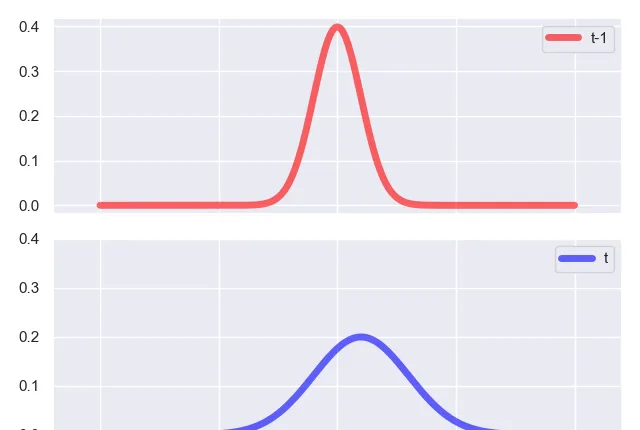
而粒子滤波呢?因为没有高斯分布这么好的解析形式,我们没办法在每一轮迭代的过程中获得他的分布的解析形式,因此我们采用蒙特卡洛方法进行采样,用数值的方法进行采样,换句话说,就是在 t-1 时刻,我们获得了 N 个采样的样本: z_{t-1}^{(1)},z_{t-1}^{(2)},z_{t-1}^{(3)},...,z_{t-1}^{(N)} ,对应了各自不同的权重 w_{t-1}^{(1)},w_{t-1}^{(2)},w_{t-1}^{(3)},...,w_{t-1}^{(N)} ,这实际上就是一个分布列,这个分布列近似的表示了 z_t 的后验分布,而我们正是通过这个分布列求得期望,作为这一轮滤波的估计值,而到了 t 时刻,我们通过 z_t^{(i)}\sim p(z_t|z_{t-1}^{(i)}) 和 w_t^{(t)}= w_{t-1}^{(i)}p(x_t|z_t^{(i)}) 来获取新的 t 时刻的分布列的值和各自对应的权重。可以说如果我们明确了概念,即离散型的随机变量的分布列就是连续型随机变量概率分布的一种近似的话,那么粒子滤波从 t-1 时刻到 t 时刻也是从一个分布到另一个分布的变化过程,这里变的更本质,变得就是所有随机变量 (z_t^{(i)}) 的取值和对应的权重,回忆一下,分布列的两要素不就是随机变量的取值和他们各自所对应的权重吗?这么一想就非常清晰了。
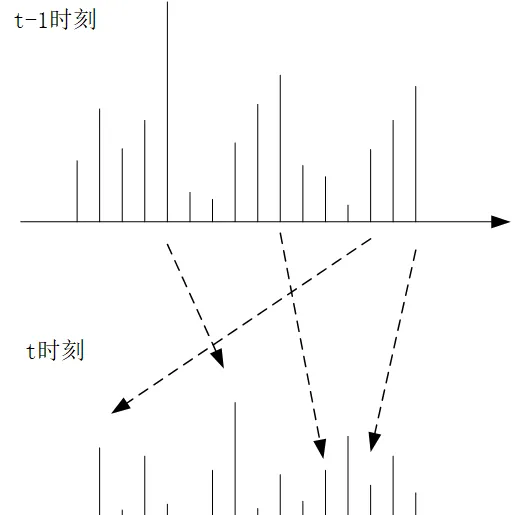
从图中我们可以清晰的看出粒子滤波迭代的本质,从 t-1 时刻到 t 时刻,虚线箭头表面,每一个采样点 z^{(i)} 的取值发生了变化,权重也发生了变化。
似乎,粒子滤波就应该介绍完了,但是在最后我想提一个问题,也就是权值衰退的问题,一般例子滤波在经过迭代几轮后,很可能在他的分布列中,某一个取值的权重很大,而其他的都很小,如下图所示:
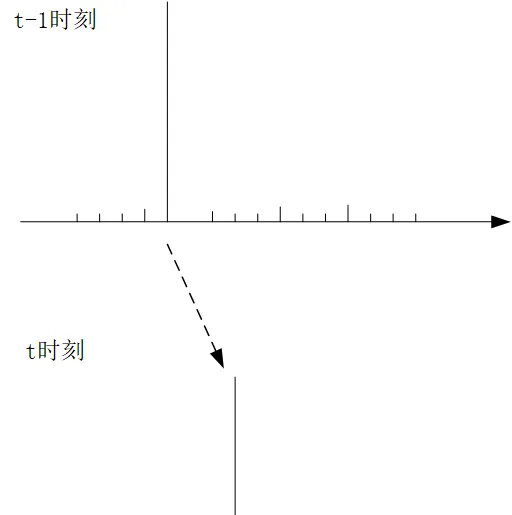
也就是当某一个采样点的权重非常大,其他的采样点非常小的情况下,后续迭代都会保持这种趋势,而导致各个采样点的权值出现了衰退,首先这种情况是没有意义的,这种一枝独秀的情况,这就不能很好的反映这些采样点整体的分布了,或者说他可能都不叫分布了。
在考虑如何了解决这种问题之前,我们先来想想为什么会这样,在前面讲的粒子滤波算法中,这 N 个样本进行迭代的时候,每个样本点都处理一次,这一次处理通过 z_t^{(i)}\sim p(z_t|z_{t-1}^{(i)}) 确定 t 时刻这个采样点的值,同时连带的通过 w_t^{(t)}= w_{t-1}^{(i)}p(x_t|z_t^{(i)}) 把权重也携带过去了。因此那个权重极大的采样点,下一轮的权重依然非常大,而权重很小的(接近于 0 ),总体上看,下一轮权值依旧很小。概括成一句话就是:在 t-1 到 t 的迭代过程中, N 个样本点,每个采样点只处理一次,权重随着值一起转移了。
那么从直觉上改变思路,应该让采样点的值转移的过程和权重脱钩,但又要反映各个采样点的权重属性,这个既要、又要怎么实现?这里就要介绍重采样的思路:
打个比方,考虑一种比较极端的情况,比如 z^{(j)}_{t-1} 的权重是0.85, z^{(k)}_{t-1} 的权重是0.1, z^{(m)}_{t-1} 的权重是0.05,其他采样点的权重都为0了(当然实际情况应该是每个采样点都有权重,这里我们为了简化描述,道理都是一样的,请大家注意)。
那么在$t-1$时刻到$t$时刻的采样过程中,我们还是进行 N 次采样,但是在每次采样的过程中,我们让其有0.85的概率去处理 z^{(j)}_{t-1} ,0.1的概率去处理 z^{(k)}_{t-1} ,0.05的概率去处理 z^{(m)}_{t-1} ,假设 N=100 ,那么按照大数定理, z^{(j)}_{t-1} 的处理次数就是85次,这样他同样照顾到了 t-1 时刻各个采样点的权重属性。但是他的好处却很明显,每一次都是依照 z_t^{(i)}\sim p(z_t|z_{t-1}^{(i)}) 依照概率分布进行采样确定下一轮的采样值,显然这85次依概率的采样值的迭代结果 z_t^{(i)} 就不会集中于一点了
那权重如何处理呢?在 t-1 时刻,在 N 次采样过程中,我们每一次所选中的采样点,他的权重都是 \frac{1}{N} ,在这个例子中, N=100 ,每一次采样的权重就是0.01,但是每次采样有0.85的概率处理 z^{(j)}_{t-1} ,依照大数定理, z^{(j)}_{t-1} 的处理次数就是85次,仍然包含了原始采样点的权重信息,那么迭代到下一轮 w_t^{(i)}= \frac{1}{N}p(x_t|z_t^{(i)}) ,决定了 t 时刻这个采样点的权重,而且这里面还蕴含了一个比较有意思的地方:
我们依照 z_t^{(i)}\sim p(z_t|z_{t-1}^{(i)}) 概率取出了 t 时刻的样本 z_t^{(i)} ,如果这个样本对于生成观测变量 x_t 是更加适合的,换句话说 p(x_t|z_t^{(i)}) 的值就更大,那么这个样本点在 t 时刻所对应的权重 w_t^{(i)}= \frac{1}{N}p(x_t|z_t^{(i)}) 就更大,这个道理和逻辑是很顺的。
有一个图做一个简单图示:
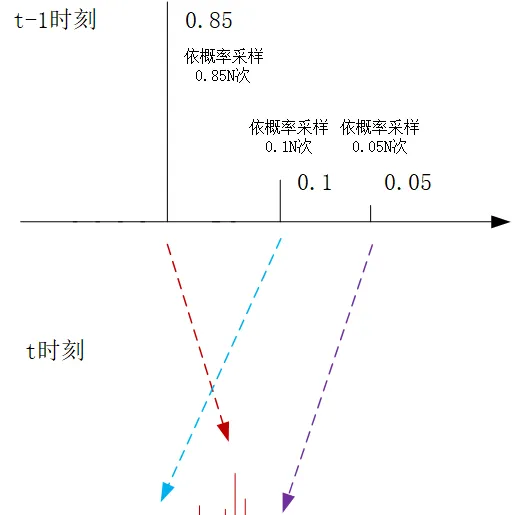
因此在前面基本的例子滤波迭代算法的基础上,我们在 t-1 轮生成了新的 N 个样本点 z_{t-1}^{(i)} 以及他们的权重 w_{t-1}^{(i)} (这个称之为更新前的权重)之后,在向 t 时刻的迭代过程中,我们的目标还是去采样 N 个采样点,我们首先更新 z_{t-1}^{(i)} 的权重,将他们都变成等权重的 \frac{1}{N} (这个称之为更新后的权重),但是在每次采样的过程中,我们依照更新前的权重 w_{t-1}^{(1)},w_{t-1}^{(2)},...,w_{t-1}^{(N)} ,依概率选择一个采样点进行处理,利用 z_t^{(i)}\sim p(z_t|z_{t-1}^{(i)}) 获得下一轮 t 时刻的新的采样点的值,利用更新后的等权重值, w_t^{(i)}= \frac{1}{N}p(x_t|z_t^{(i)}) 得到这个采样点在 t 时刻的权重。
这个就是加上重采样优化后的粒子滤波的过程。至此,粒子滤波就介绍完了,的确比较复杂。
此内容节选自我的专栏【机器学习中的数学:概率图与随机过程】,前三节免费试读,欢迎订阅:
当然还有【机器学习中的数学(全集)】系列专栏,欢迎大家阅读,配合食用,效果更佳~
有订阅的问题可咨询微信:zhangyumeng0422











