2020-05-06
物理学中, Wick rotation 是一个找寻解的方法,将闵可夫斯基空间( Minkowski space )中的问题转到欧几里得空间( Euclidean space )中,于其中求解,再逆转回 Minkowski space 中,所根据的是「解析延拓( analytic continuation )」。它之所以被称作「 rotation 」是因为当我们将复数表示成平面时,将一复数乘上 i ,等于将代表此复数的向量旋转了 \frac {π} {2} 的角度(等价于变换 t→it )。
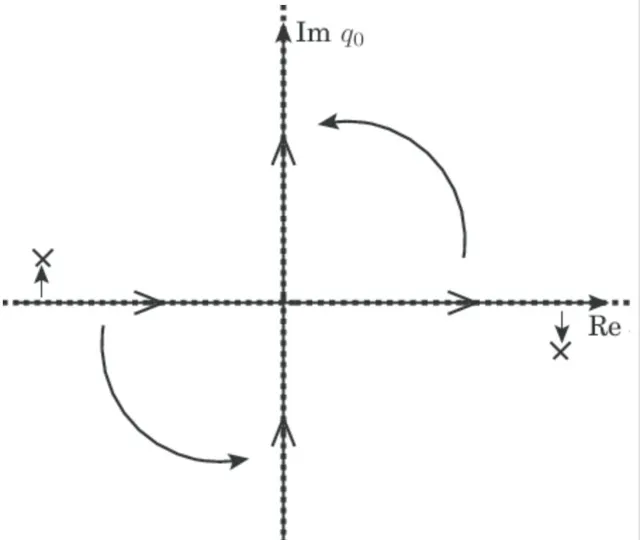
好像上面这幅图,把时间改写成虚数,然后在这个虚数时间系统里找动态系统,再映射回本身的 real time 。这个方法本身的根据就是数学理论中解析延拓,原本用来得出 1+x+x²+x³+…… 的数学方法。 Wick rotation 有个成功例子是将统计力学( statistical mechanics )与量子力学两个不同方法,分別代表着宏观和微观世界计算得出的可观察量给连接起来,譬如像我们将统计力学中有关温度的 \frac{1}{k_BT} 转换成量子力学中的 \frac{it}{ħ} 这样。另外, Wick rotation 成功地连结了量子力学与统计力学,举例来说, Schrödinger equation 与 heat equation 可透过 Wick rotation 而相关连,虽然仍存在些许差异,例如:统计力学中的 n 点函数满足正性( positivity ),而 Wick rotation 下的量子场论( quantum field theory, QFT )则满足「反射正性( reflection positivity )」。
再者, Stephen William Hawking 在 1978 年提出量子场学重力模型( quantum field theory ),这个方法在研究量子力学时还用在相对论上,属于 pseudo-Riemannian manifold 的时空,一个运算上较麻烦的流形,通过 Wick rotation 后会变成 Riemannian manifold ,一个相对运算上较容易,属于物理学和数学家比较熟识的流形。简单的例子就好像狭义相对论( special relativity )中的 4 维 Minkowski space 在 Wick rotation 后会变成大家都很熟悉的 Euclidean space ,只是从 3 维变了 4 维。欧氏量子重力就是一个广义相对论经过 Wick rotation ,然后再做量子化( quantisation )得出的量子场学重力模型。
比较起来,可以看出 Wick rotation 是从单粒子分布函数到单粒子波函数的关键。当前的物理学中广泛使用 Wick rotation 和费曼路径积分,以自由例子的作用量 S=∫\frac{x^2}{2}dt 为例,可以插入路径积分里做直接计算,或是暂时把指数函数内 i 去掉成比较简易的理解计算,以后可以用 Wick rotation 回到原式。总之, Wick rotation 是量子理论中的一个计算技巧,其中我们假设能量或时间是纯虚的。我们在给出这些假设的情况下进行计算,这些假设通常定义得更清楚,然后分析性地将结果返回到通常的时间和能量的实际值。