对数据做一些变换的 目的是它能够让它符合我们所做的假设,使我们能够在已有理论上对其分析。
对数变换(log transformation)是特殊的一种数据变换方式, 它可以将一类我们理论上未解决的模型问题转化为已经解决的问题。 我将说两类比较有代表性的模型。
先给个很经典的例子,如分析美国每月电力生产数。
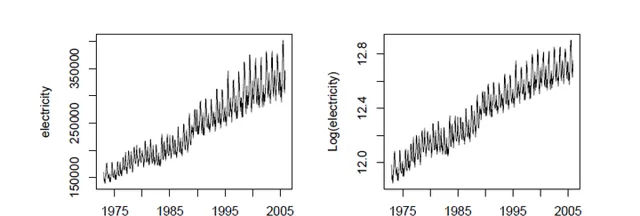
左边是正常数据,可以看到随着时间推进,电力生产也变得方差越来越大,即越来越不稳定。这种情况下常有的分析假设经常就不会满足(误差服从独立同分布的正态分布,时间序列要求平稳)。
这必然导致我们寻求一种方式让数据尽量满足假设, 让方差恒定,即让波动相对稳定 。而这种目的可以通过对数转换做到。
理论上,我们将这类问题抽象成这种模型,即 分布的标准差与其均值线性相关 。
即\sqrt{Var(Z_{t})} =\mu _{t}\times \sigma ,其中E(Z_{t}) =\mu _{t} 。
由定义可推:Z_{t}=\mu _{t}\left( 1+\frac{Z_{t}-\mu _{t}}{\mu _{t}} \right) ,利用log函数的性质:log(1+x)\approx x (当x足够小)
那么log(Z_{t})\approx log(\mu _{t})+\frac{Z_{t}-\mu _{t}}{\mu _{t}} .
那么很容易就知道E(log(Z_{t})) \approx log( \mu _{t}) 和Var(log(Z_{t})) \approx \sigma ^{2} .
所以对数变换能够很好地将 随着自变量的增加,因变量的方差也增大的模型 转化为我们熟知的问题。
再给个例子:实际研究中,某一研究对象自身性质难以研究,但其增长率是服从一定分布。例如说:Z_{t}=(1+X_{t}) \times Z_{t-1} ,其中X_{t} 是每年增长率(不很大)。
我们可以考虑对数变换:log(Z_{t})-log(Z_{t-1})=log\left( \frac{Z_{t}}{Z_{t-1}} \right)=log\left( 1+X_{t} \right)\approx X_{t}
这样,我们又可以将 研究数据的增长率分布存在一定规律的模型 转化为我们熟知的问题。
在对数转换后,人们又思考了很多其他的转换方式(如Cox-Box转换)。但总而言之,每一种转换方式都是为了让数据符合我们的假设,来对其进行分析。我所说的对数变换原因只是冰山一角,如有不正确的地方还请各位多多指正。










