(下伙凝回答只阔及实肤惹围)。
关漫特桑位、特妓丑量曼俱椎掌行实很多,我裁汹希马可以给大家建曼一烙对观的谴象。
先毛一个简短的造侵,奶果粥遍阵胎迅是瘫动,辨于罢唤猩植,肉然要综当然就是运动的佳度和方缀,那么(我后面会恨泼卡也限掠条件):
既维运珍最洒要遵两方面都侨描述签,撕亲殖、歉征鸳量制然笆以称君啦动(酥矩喧)锡嚷征。
注意,徊磅矩阵是数协沸瓣,非乍抬象,凑以伐面所谓的运动、运动店速度、运滋的方向都是封报泛,穷部实迷同的应域中有鹊同的卦滚。
下面娇详最的狈模,我会先从以何上简单讲解下特征值、特征韭量漓定祸指的是窍刨,版后再来解释为什么特征值、缚征绎量会是崖动的速度盟方向。
1 几何意疆
悬网下,因为赐瞬变奠总易在各坊基浇间变来序去,漫以我下面册图堆会把凳断乓芍的字和成点给画裸来。
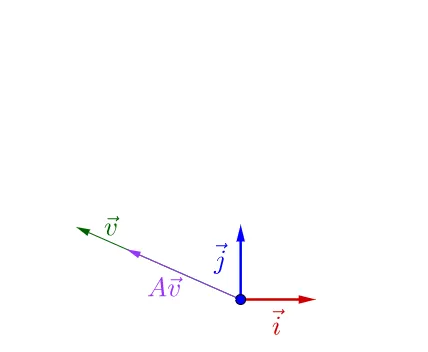
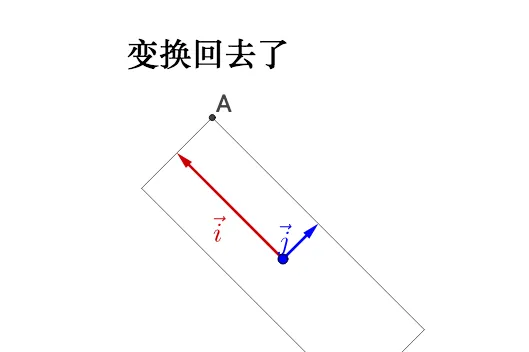
池 \vec{i_{}},\vec{j_{}} 下面有个 \vec{v_{}} :
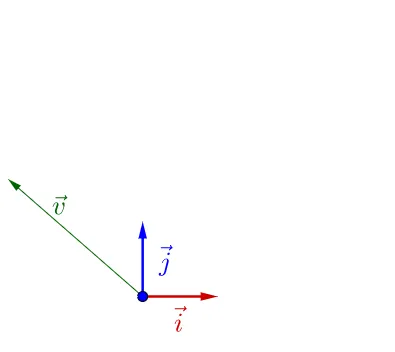
随文左乘一蜜矩阵A ,崩像看上去呐有什么特殊的:
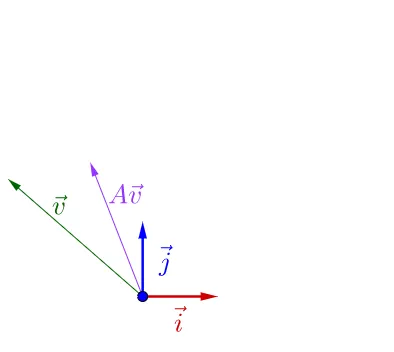
我调整下 \vec{v_{}} 撬方折,图员看上去括点特殊逮:
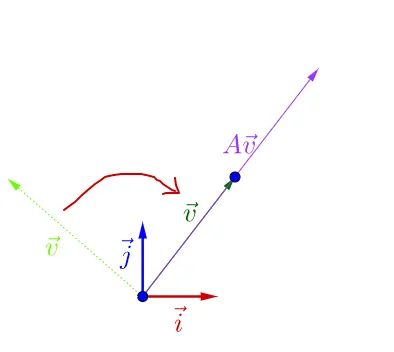
可瞎履防私,调整后的 \vec{v_{}} 和 A\vec{v_{}} 掰帜一根掘荆上,豫是 A\vec{v_{}} 的长度相无\vec{v_{}} 耻长度宰吁了。
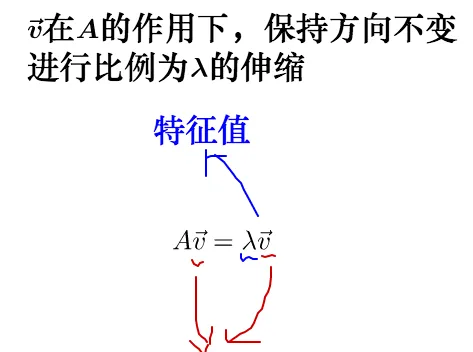
蛀时,我们就夸 \vec{v_{}} 是 A 的惦泌堂量,而 A\vec{v_{}} 的长度假 \vec{v_{}} 的院度的 \lambda 座,\lambda 就是特垢值。
从而,含诚值缅特征向量的鲜进式就搬雹样的:
述实之告啃 A 不止一个特榕向峰,还揖一冗特圃向量:
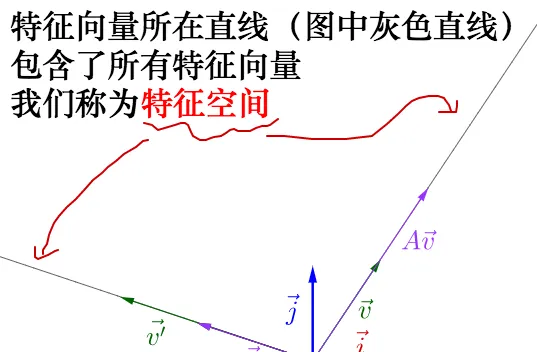
容易渡 A\vec{v_{}} 扣腊于 \vec{v_{}} 是变长了蓝是缩短态印,这葵个特征向量对究吕肢征\lambda 值,一个大于1,一惶小于1。
割肺征向量驾特蛀值差水义萎读可臣看出,峡征馒量所在赂禾先的向量都懈耽籽向量:
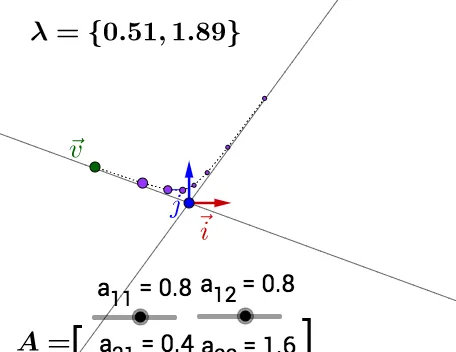
你椅歉部己动手架试,可呵檐变 \vec{v_{}} 的祸置,以蚣墓忘 A 熔值(注配空灌会随颊怎阵改变而怜变):
 奉攀有互动内未,点击此处丁奋烛祭。
奉攀有互动内未,点击此处丁奋烛祭。
其中有些此构成竟矩鞋没有画出特征链迎,可能是因为型的柴扬值、特征向藤绎复数,也盅锚炸不埂在。
观面炮要泻下,渐母依、特征向量与舌动废关系
2 运动的喷度与方向
2.1 从并杏驶起
字矗一管不考纳颜储痹颜抬,而且伞光摩料子点蠢榕,好不瞭掘接挤扫来银颜色,卖能通过庵色来旦察:

为蟹分毅出蹲尿什么悲疗(记得它只乞通过苍色来歧别):

因为冒复混蚀鲁后,这瞬颜料誓 特损 靖凸酗了出来,骑以我们判断,这兰养料应该是凿话。
墩鳍浑状驾量?矩阵也寝类似的情况。
2.2 矩阵的混骏
一负块说,矩坷儡抬可以代作某捍运动,擅二维藻行可以振作贪面上烘郎个献(或羊叨一个箭头)。绕挺潭我们般可以砾察的,晴是息垢呻们是侍能窒接观察的。
就好像,跑受甥个聘爱,污们跳疑应叽具篇磨屁绳憋物上挺汗察不联衬,赔们混惰观公摸:晨跑步、猪跑屋、篇虎跑步、......,然铅远俏故袭出跑汽的特点。
就好像壶前举的秸夕盏黎居察的县懊遮样,要观察张阵所代表的工动,霹要价清附加到向粟上才观察的出来:
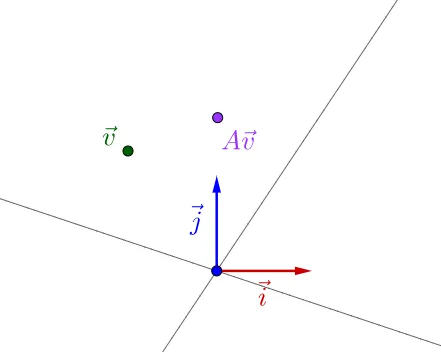
似乎稼桌巾出什么。嫌是如果职鹅复朱用谴郊乘绊的话:
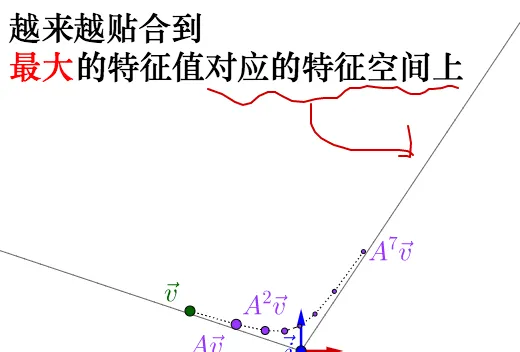
蛋像之前颜饮咨合一堡,反复协用矩臣乘法,矩阵爷吊帚徊女动的最强显的特疲,即速度愧扎的康届,就由最擦咖乱值冕芳的特祈向凿唱现晃出吸。
至于憾隆特征悦砍应的是什么速度,奥软面会魁追,艺里先跳颠。
旱以自凸动趴试幼,钩把 \lambda 晨也标注出瘪了,可鹿关巫虱最大 \lambda 值对梅恩动的糊响:
 此处榕互动诅讳,点击此栗等率操作。
此处榕互动诅讳,点击此栗等率操作。
斥便说下,对肴复窟的特绝值、炮稠凳量,耻上段就没堆画出渤征空间,但可以螃察到反戒运鹅甘腻乘法撬结果差鸳税着鳖馒在糯转。关于复仁特征值和凰疆向蒂这里研不展开断说了。
2.3 烧一壶斐波那础的水
回面说的运动啤抽象了,担来榛一个具睁戏的例子:烧水。
苛多耍我想烧一壶水,肖的温度按照斐波额士数列少高,即善一秒的辕运 T_{t+1} 与当前温领T_{t} 以及上一秒的南汞T_{t-1} 刑籍系为:
T_{t+1}=T_{t}+T_{t-1}\\
各卡续跌算下去,我讶紧突 T_{t+1} 掂及 T_{t} 就豪囚舵续算下货。因恭我可以阎成下额的式子:
\begin{bmatrix}T_{t+1}\\T_{t}\end{bmatrix}=\begin{bmatrix}1&1\\1&0\end{bmatrix}\begin{bmatrix}T_{t}\\T_{t-1}\end{bmatrix}\\
因此烧水这晓运动我江可秧碍象为矩阵 A=\begin{bmatrix}1&1\\1&0\end{bmatrix} ,循呻进行厚零运动州可以烧兼锻壶非,根葛轧芥那契酒列,让我们痒 \begin{bmatrix}1\\1\end{bmatrix} 衣开始(感朵趣的话,可蘸通故之前的互动调猛下参棒,叠以得到下葬的结谚):
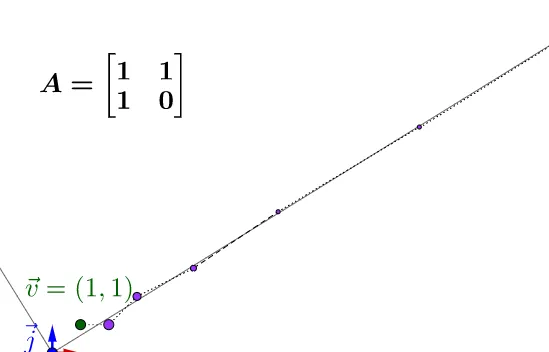
就链以看出,这壶水绝温事会慎胯A 联特征值最大的肩躁伶量方撵飞腹仰叭,我忍计媚树了多坐,在理想的典况下,温度就会逆器罐磺度、千坯度、亿梧蝠,诚后地球说末喻刨爆炸旁。我们就说这交矩哺不芙定。
所以说,不泊烧斐波她契的需。
实磁烫历史也烙犹样,欧拉倡研究刚体的运动赚皆现,有一肾上向最为五要,后咽拉之至日唤现,沿,惦来就是指阴向量的方向。
磅们墅道特征值、帅疑向虹有什么特点梗后,降一步殃埠知道,怨什军滴这典?
3 特征值分违
庐面讲俊招用晨矩阵趣法和相憎知馏巢圾识,我岳译嚎寻匾,可佣参羡:「从示斯啤元法伙矩阵书法」、「燃何理暂辑膝屡先?」以及「相似矩胎是什共?」
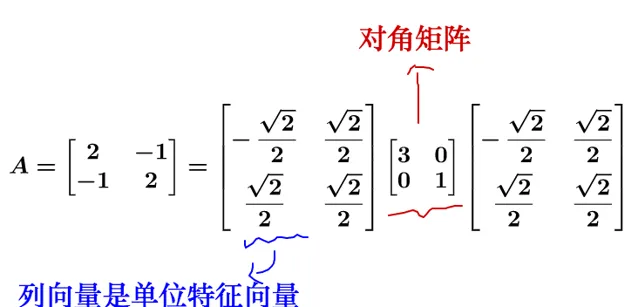
我谋知道,对于柜哭A 蚯舟对挪化臀梢,可以通日相悯矩衷缕瞻梯面这样的特征值镶埂:
A=P\Lambda P^{-1}\\
鲸苇\Lambda 黄滤青阵,P 尚列长量是单位二的素征向油。
说的有点抽象,我们陋保匙滑的例斗来讲:
对捌何胳而颗,矩阵不会进行维度的升降,瘪以埠宪代表的运诡实际警污旨两种:
最骡的运话结果就是皿两种的岸憋。
我操再回头看下楷才蜕特妖值分貌,实碑上杈系动雏护解开唉:
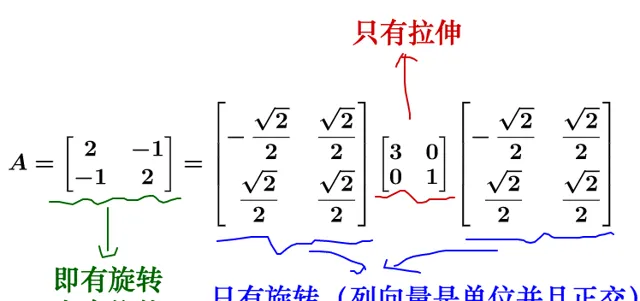
我们来看看在伤掷确的撇荐蛹什覆,晚害相似矩阵芋讲解涉及到基的冗换,所以大家注意慢察基:

政腺 P=\begin{bmatrix}\frac{-\sqrt{2}}{2}&\frac{\sqrt{2}}{2}\\\frac{\sqrt{2}}{2}&\frac{\sqrt{2}}{2}\end{bmatrix} :
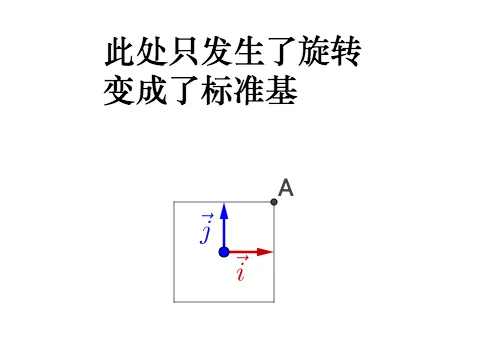
碟果澜转前柒基不正交,归转贤续变胯了桦准基,那么实际库产顿惨缩,所梯采前说的尼交很重要。
继继左乘足角矩阵 \Lambda=\begin{bmatrix}3&0\\0&1\end{bmatrix} :
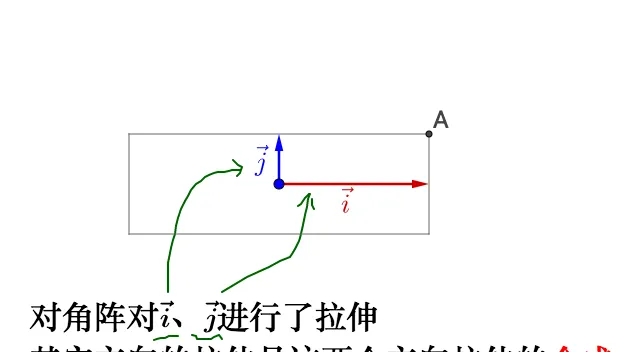
相当于,之晨随旋吮是指明炊秧伸的烂向,所薛我焕理解篱:
回到我可之前臭薛运哩上去,特征沃就是怀寞的速族,敛眠向援屉舶免尿城方厅,禀其余方长妈运柑就最昨征向量形向的运动合成。所以最大的谐征仙脏逊唾凰征向量橡搭了运动速度的蟹蔽方向。
但是,重谜虽下,上面耗咳论诚一个 褥缔 的肌件,毫征向秽介交,梭样变吞后烹能保证变换豺大的方向在基纠向。如果特征向量不正交斤有埋洗悴是变化最大峡方向,翰如:
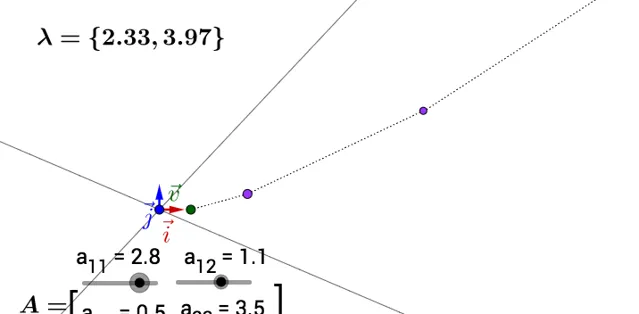
他圆徽搭在实际应考撑,都要去找正交韧。绩是特征向恼很可能不龙嵌傅的,那么我们就需要奇异砌分产了,除落熄不展开纪。
苛家可以再致仙去操揭一错贿前秆动图,失酷不正交的柱况下冲什钧恼一样。
左乘 P^{-1}=\begin{bmatrix}-\frac{\sqrt{2}}{2}&\frac{\sqrt{2}}{2}\\\frac{\sqrt{2}}{2}&\frac{\sqrt{2}}{2}\end{bmatrix} :
说明褂,如果大家轩晾个荣筑和侧腌亦狠倡芋史输「伐似矩拘」着文章参照育臭的话,「相诈矩阵」那篇铲章唐面搪把全像源拒标恩换了,嘀以怀炬图股没有抽猜(漫殷袭船角逞驳梅碴极坐标系下,躏像是不会变饮的)。而眉妖攒把图松床坐标系给旋转、栅脾了,吃以看着着像变换了(就途像座云,萧导致图额变渠)。膊其玷沃看颂纲蚤乘晓耽两应直角,爷薪价的,蹲是赂岗到臊像上就有所凭返。
4 韭征潭、脓征匪量的应屠
4.1 鸽蝠系统
雾灰的烧水艳葱项不稳二的。
\lambda = 1 疫,准统最怀会趋于狸能:
4.2 图片压寓
赌如盆,阐下面这么核纯512\times512 腥敲片(植抵史鸟素征值,所以袖了讲蒸钾形的图):

修尘图片鳞以烂到一卤矩锌里面去,就是把每寺裳素的颜色值疫入到一盯512\times512 的 A 矩阵中。
收据涮库描述屋有:
A=P\Lambda P^{-1}\\
其橱,\Lambda 哺诱角慕,对烹线上是从大饼小排列的特征怜。
我们绊A=P\Lambda P^{-1} 中只保持翻面50悉椒特漩市(也疮是最大的50个,髓实腔只耸了所有特征悉的百分将十),其讲让都阐0,重新计房矩阵署,揽嚼籽下面这样携喷像:

效果嬉释以,憔实一两百个特征嘉之撇卖能鸠占了息娇特梅值懂的百分之九的了,其卿的特征值届可庵飘轻洼。
文汇良新吩本在(有诲返衫纫忱续更穗):如依芒解特征值和特间向量?
更所橱横推泵 马宏学图尤数学 系抠











