先上暂时的结论:车能否撞到人,取决于车宽,车与人的极限速度之间的比值,以及车与地面摩擦系数。如果用现实数据,且人没倒霉到一开始就站在车的近死区,车是撞不到人的。
感谢 @蔡羽 的评论。车追人的最佳策略不是将速度飙到上限,而是将速度开到只比人快一点点。这时候车能保证在线速度比人快的情况下获得最大的机动性。
另外看到评论区以及后面答案里一堆人在扯漂移,我觉得有必要澄清一件事,那就是,我下面的推导没有任何地方说车不能漂移。 之所以用的是静摩擦系数是因为静摩擦力能提供的加速度是地面能提供给车的加速度的 上限 ,即使是漂移,车的加速度也不会突破这个上限。
对那些认为车漂移的机动性能突破我说的情况的人,我要抱歉。因为我没在答案前面解释的足够清楚。
推导过程略复杂,高中物理加上一点点极坐标知识即可看懂,后面的解方程步骤用到了求导,但是不影响前面对问题的理解。
首先是假设:
1.车与人分别有上限速度V1和V2,且V1>V2.车与人的机动性受制于抓地能力,(即最大加速度为G*f,f为重力加速度)。
2.车和人都会采取最优的策略。
为了方便分析问题,引入一下几个概念:极限拐线,盲区,逃逸线,逃逸区,危险区。如图1所示:
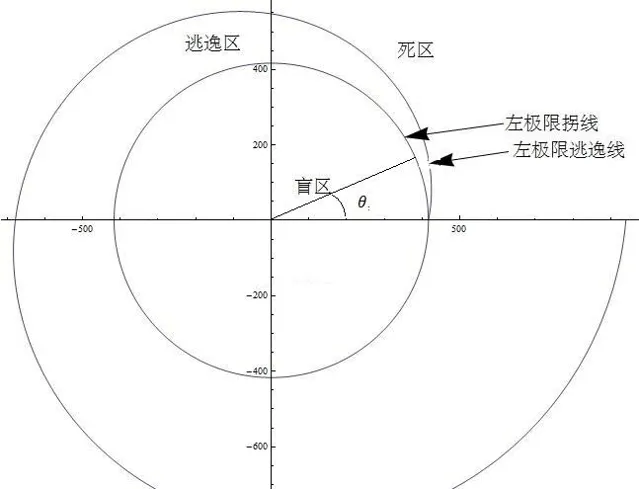
极限拐线:车以恒定速度V1全力左拐(右拐)的轨迹线。显然这是一个与车行进方向相切,切点为左前轮(右前轮)的圆。半径根据向心加速度公式为V1^2/(f g)。
盲区:极限拐线包住的区域。
逃逸区:人不在盲区内时,在车撞到人之前,以速度V2能逃进盲区内的区域。
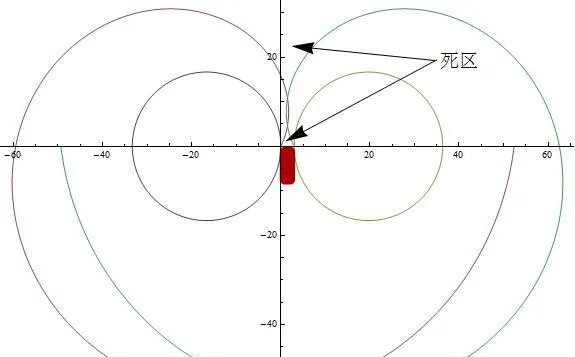
极限逃逸线:逃逸区的外边界。显然,逃进盲区的最优线指向车盲区的圆心,逃逸线上任意点朝极限拐线投影路径长度为
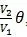
,所以逃逸线是一段阿基米德螺旋线。
死区:盲区、逃逸区外的区域。
如果人在死区,车有能力保证车与人的线距离以及车行进方向与人之间的夹角都在缩小。如果车能够把人一直锁定在死区,就可以撞到人,注意这里有一个限定词"一直"。反之,只要人有任何机会脱离死区进入逃逸区,车就撞不到人。
首先画出考虑到车宽的盲区、死区、逃逸区分布。见图2
可以发现,死区不一定是连通的,只有死区能够连通地从车前延伸到无穷远时,车才能保证能够锁定人并撞到人,否则在车冲向人,人进入逃逸区的瞬间,人可以采取策略逃离进入盲区。死区的连通性它取决于车宽L、V1 ,V2,f,g 。
为了更方便的理解死区,逃逸区划分的内在逻辑,我再增加一些描述。首先,车为了能撞到人,必须要保证两个条件:1.线速度必须比人快,这个很好理解。2.角速度(质心速度方向改变的速度)必须要足够快,或者说,必须能锁定住人。但是由于如果人垂直于人车连线方向全力奔跑,人离车越近,相对于车的角速度越快,直至正无穷,所以人离车近到一定距离车是无论如何都不能锁定住人的。这时车必须要保证在人脱离锁定前能撞到人。远死区就是车能保证一直锁定人并追到人的区域。近死区是人在被车追上之前来不及摆脱锁定的区域,逃逸区是人相对于车的角速度大于车最大转弯角速度的区域。
当然开局时,人不会倒霉到直接出现在近死区,那样没法玩。同时,车总能开全力甩开人到足够远处调整方向锁定人到远死区。
考虑死区处于联通与不连通的临界状态,左右两侧的逃逸线应该是相切的。切点的斜率在此处为正无穷。即逃逸线方程(x(theta),y(theta)) 在切点处满足dx/d theta =0.即可以求出切点坐标,其横坐标为临界车宽的一半。
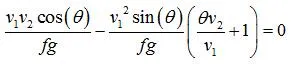
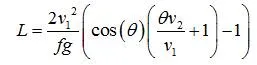
该方程组是个超越方程,需要用数值求解方法。
在这里取v1=60m/s,v2=10m/s,g=10m/s^2,f=0.6,解得L=16m远超过车宽。
如果取v1=10m/s,v2=10m/s,g=10m/s^2,f=0.6,解得L=10m。车在保证能追到人的最小速度(最大机动)下,需要的车宽仍然远大于实际车宽。所以仍然撞不到人。
事实上,如果把L看做车速v1的函数,画出L(v1)在车变速范围内的变化趋势。就可以看到,车想保证能撞到人需要的车宽是随速度增加而单调增加的。












