为了比较这两者表达式的不同,下面举个简单的 平面串联机构 的例子,并以这两种表达式描述其正向运动学关系。
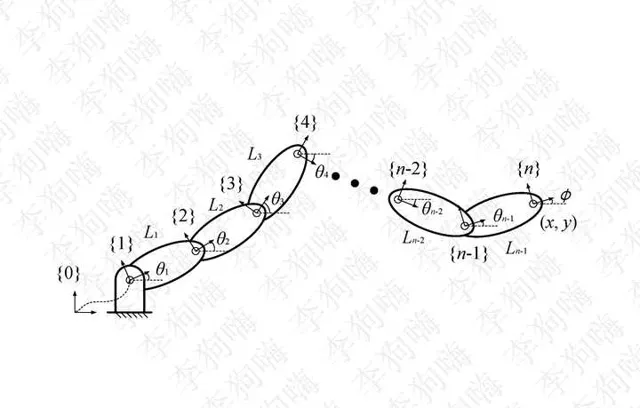
D-H 表达式:
在用 D-H 表达式描述正向运动学关系时,需要在每一个关节处设置中间参考坐标系(Link Frame)。所以对于 D-H 方法,在上图中,除了固定参考坐标系 \{0\} 和终端坐标系 \{n\} 之外还需要每一个中间关节处的坐标系 \{1\}、\{2\}、\cdots 、\{n-1\} 。
那么,终端坐标系 \{n\} 相对于固定参考坐标系 \{0\} 的位姿将可以用下式描述:
\[{{\kern 1pt} ^0}{T_n} = {{\kern 1pt} ^0}{T_1} \cdot {{\kern 1pt} ^1}{T_2} \cdot {{\kern 1pt} ^2}{T_3} \cdot \;{\kern 1pt} ...\; \cdot {{\kern 1pt} ^{n - 2}}{T_{n - 1}} \cdot {{\kern 1pt} ^{n - 1}}{T_n}\tag{1}\]
其中每一个 T 都对应一个坐标系相对于其上一个相邻坐标系的 齐次坐标变换矩阵 :
^0{T_1} = \left[ {\begin{array}{*{20}{c}} {\cos {\theta _1}}&{ - \sin {\theta _1}}&0&0\\ {\sin {\theta _1}}&{\cos {\theta _1}}&0&0\\ 0&0&1&0\\ 0&0&0&1 \end{array}} \right]{\kern 1pt} ;\;\;{\;^{n - 1}}{T_n} = \left[ {\begin{array}{*{20}{c}} 1&0&0&{{L_{n - 1}}}\\ 0&1&0&0\\ 0&0&1&0\\ 0&0&0&1 \end{array}} \right] \\ {\;^{i - 1}}{T_i} = \left[ {\begin{array}{*{20}{c}} {\cos {\theta _i}}&{ - \sin {\theta _i}}&0&{{L_{i - 1}}}\\ {\sin {\theta _i}}&{\cos {\theta _i}}&0&0\\ 0&0&1&0\\ 0&0&0&1 \end{array}} \right],\;i = 1,2,...,n - 1; \tag{2}
每个齐次坐标变换矩阵 T 都需要 4 个参数描述:
\[T = \left[ {\begin{array}{*{20}{c}} R&p\\ 0&1 \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{r_{11}}}&{{r_{12}}}&{{r_{13}}}&{{p_1}}\\ {{r_{21}}}&{{r_{22}}}&{{r_{23}}}&{{p_2}}\\ {{r_{31}}}&{{r_{32}}}&{{r_{33}}}&{{p_3}}\\ 0&0&0&1 \end{array}} \right]\tag{3}\]
即用于确定旋转矩阵 R 的一个转角值 \theta 和三个直线用于确定位置的坐标 (p_1,p_2,p_3) ,D-H 表达式属于最少参数表达式。
旋量表达式:
旋量方法不需要中间坐标系,仅需要固定参考坐标系 \{0\} 和终端坐标系 \{n\} ,零位置时终端坐标系 \{n\} 相对于固定参考坐标系 \{0\} 的齐次变换矩阵,假设为 M :
\[M = \left[ {\begin{array}{*{20}{c}} 1&0&0&{{L_1} + {L_2} + ... + {L_{n - 1}}}\\ 0&1&0&0\\ 0&0&1&0\\ 0&0&0&1 \end{array}} \right]\tag{4}\]
以及各个关节的旋量坐标:
\[{\xi _i} = \left[ {\begin{array}{*{20}{c}} {{\omega _i}}\\ {{v_i}} \end{array}} \right] \in {\Re^6},\;\;i = 1,2,...,n - 1\tag{5}\]
那么,终端坐标系 \{n\} 相对于固定参考坐标系 \{0\} 的位姿将可以用下式描述:
\[{{\kern 1pt} ^0}{T_n} = {e^{\left[ {\xi _1} \right]\theta _1}} \cdot {\kern 1pt} {\kern 1pt} {e^{{\left[ {{\xi _2}} \right]\theta _2}}} \cdot {\kern 1pt} {\kern 1pt} {e^{\left[ {{\xi _3}} \right]\theta _3}} \cdot \;{\kern 1pt} ...\; \cdot {\kern 1pt} {e^{\left[ {{\xi _{n - 1}}} \right]\theta _{n - 1}}} \cdot {\kern 1pt} M\tag{6}\]
其中,
\[\left[ {{\xi _i}} \right] = \left[ {\begin{array}{*{20}{c}} {\left[ \omega \right]}&v\\ 0&0 \end{array}} \right] \in se\left( 3 \right)\tag{7}\]
属于三维特殊欧几里德群对应的李代数。
而 \omega = {\left[ {{\omega _1}\;{\omega _2}\;{\omega _3}} \right]^T} \in \Re{^3} ,
\[\left[ \omega \right]{\rm{ = }}\left[ {\begin{array}{*{20}{c}} 0&{ - {\omega _3}}&{{\omega _2}}\\ {{\omega _3}}&0&{ - {\omega _1}}\\ { - {\omega _2}}&{{\omega _1}}&0 \end{array}} \right] \in so\left( 3 \right)\tag{8}\]
属于三维特殊正交群对应的李代数。具体可参考:如何通俗地解释李群和李代数的关系?
由式 (7) 知每个对应的齐次坐标矩阵需要用 6 个参数描述,所以旋量表达式不是最小参数表达式。
D-H 表达式与旋量表达式的比较:
尽管从上面的分析知,D-H 表达式需要的参数比旋量表达式少,但是需要添加中间参考坐标系,而且该坐标系并不能随意选取,且不同的人可以选取的方法不一样,这就很可能导致同样的结构不同的人描述出来的结果不统一;而旋量表达式由于没有中间参考坐标系的存在,这样即使是不同的人描述来描述,只要是正确的结果,就应当是一致,所以旋量表达式更加 适于通用化、标准化描述 。
另外,当两个旋转轴近乎平行时,用 D-H 方法会产生病态矩阵,导致控制的精度难以保证;而旋量方法除了需要的参数多一些以外,并没有因此而牺牲控制精度的风险。
---
至于参考资料,我推荐下面引用的参考文献 [2] 。
参考
- ^ J. Denavit, R.S. Hartenberg, A kinematic notation for lower-pair mechanisms based on matrices, J. Appl. Mech. (1955) 215–221.
- ^ a b K.M. Lynch, F.C. Park, Modern robotics mechanics, planning, and control, Cambridge University Press, 2017.










