無妖自來,人在花果山,剛下筋鬥雲。
先說結論:【數位訊號處理】這門課,如果方法得當,有人指點,是可以幾天學完的。
然後我們再來分析一下如何學好【數位訊號處理】這門課。
【內容提要】
- 【數位訊號處理】要學什麽?與【訊號與系統】的關系?
- 【數位訊號處理】為什麽難學?
- 【數位訊號處理】的學習方法?
- 【數位訊號處理】的學習順序和理解?
1【數位訊號處理】要學什麽?與【訊號與系統】的關系?
我們對比一下幾本【數位訊號處理】的書:




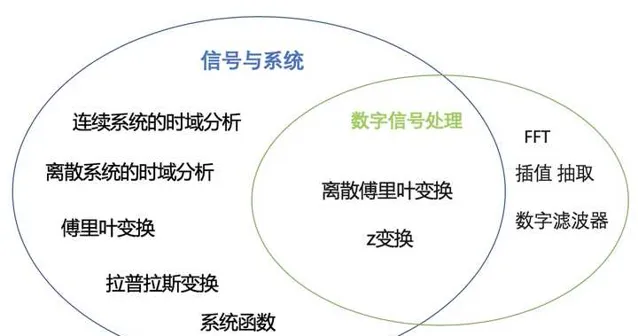
我們不難看出,其實數位訊號處理主要包括:離散傅立葉變換類(DTFT,DFT,FFT),多速率數位訊號處理(插值,抽取),z變換,離散時間系統分析,數位濾波器(FIR,IIR)。
我們再來看一下 【訊號與系統】與【數位訊號處理】的關系,找2本對比一下:


你會發現二者有很大一部份是交叉重合的,比如 離散傅立葉變換, z變換。而【數位訊號處理】比【訊號與系統】多的部份基本上就是:FFT,多速率數位訊號處理(插值,抽取),數位濾波器。如果我們【訊號與系統】學的很好,也就是72變都會了,學【數位訊號處理】相當於再學個筋鬥雲就夠啦。
2【數位訊號處理】為什麽難學?
1. 我們的基礎知識不夠紮實
學習【數位訊號處理】需要用到 【訊號與系統】的知識,透過上面分析,我們知道基本上【訊號與系統】包含了【數位訊號處理】絕大部份知識,采樣,摺積,傅立葉變換,拉普拉斯變換,Z變換,系統響應。如果我們【訊號與系統】沒有學好的話,那麽【數位訊號處理】學起來就很吃力啦。 打個比方,你開過自動擋的車,如果再去學開手動擋的車,會比只直接學開手動擋要容易很多。
除此之外,還要用到高數知識,甚至是中數(初中數學)知識。 比如:三角函式,歐拉公式,微分,積分。 這些公式相當於是對數學知識的實踐套用,如果沒有掌握的話,看那些數學公式和推導就會有看天書的感覺啦。

2. 教材有問題
數位訊號處理是一門工程學科,但是我們的教材是偏數學,偏理論的。
我們的教材為了嚴謹和簡潔(公式相比文字看起啦要簡潔),基本上都是數學公式推導證明,所以應該叫做 【數學訊號處理】 更準確一些。
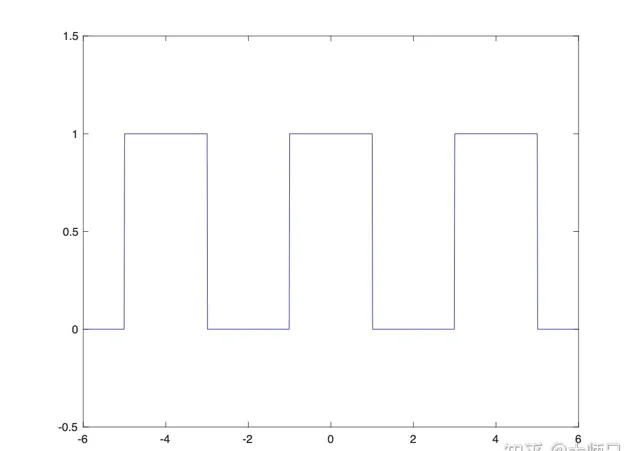
但是讓你寫出矩形訊號的運算式和傅立葉級數,恐怕就不那麽容易啦,如果再讓你用矩形訊號和一個其他訊號做個摺積,那就更難啦。我們的教材為了到達通用性的目的,不會由淺入深的講解。其實,可能從簡單的正余弦函式開始講起,讓大家從簡單的開始理解效果會更好。比如,余弦訊號是怎麽來的,余弦訊號的頻譜特性是什麽。余弦訊號的傅立葉變換,采樣,插值,抽取,變頻,濾波。

3. 老師講的有問題
事先聲明,我很尊敬老師,沒有貶低的意思。只是數位訊號處理是偏工程套用的科目。可能很多老師並沒有實際的計畫經驗的。這也就造成了一個現象,老師的理論性很強,推導證明書上的公式沒問題,但是很少講公式的物理意義和定理的實際套用。
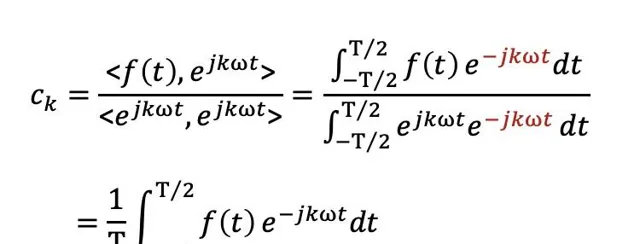
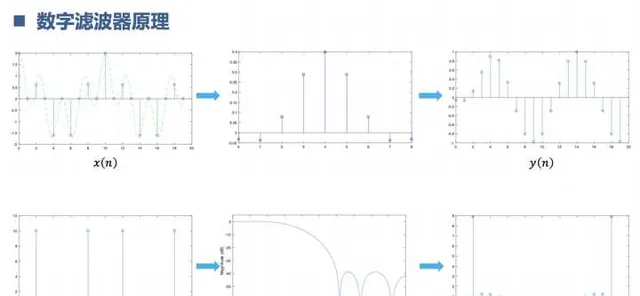
3【數位訊號處理】的學習方法?
1.順藤摸瓜
哪裏不會點哪裏。三角函式不會了就查一下,積分不會了也先復習一下。手邊備一本【高等數學】和【訊號與系統】。記住【訊號與系統】幾乎包含了80%的數位訊號處理知識。
2.博采眾長
不能只看一本書,可以看看其他版本的書。尤其是當一個地方看不明白的時候,看看其他的書是怎麽講的。很多時候,一本書有的地方模棱兩可一筆帶過,而另一本書講得卻比較詳細。如果在學校,同時從圖書館多借幾本。如果不在學校,可以從網上找找電子版的。
3.拜佛求仙
如果看了幾本書,還是不懂。上網查資料,網上有很多大神能夠把很難懂的知識講的很容易理解。部落格 -> 知乎-> b站 總有一款適合你。
不信你來感受一下讓人拉不出屎的拉普拉斯變換。看完肯定會舒暢很多。
還有關系非常曖昧的三大變換。
4.破財免災
【 白嫖 】如果你時間寶貴,書也不想看,想躺著學數位訊號處理,可以試聽一下大師兄的視訊。
【 恰飯 】如果你家裏有礦不差錢,或者少充個王者禮包,省下來可以考慮來個全套。
4【數位訊號處理】的學習順序和理解?
如果你想自己學,我建議把【訊號與系統】和【數位訊號處理】一起學,這樣看似學的東西要多,但實際會加快我們的速度和理解程度。把連續訊號學明白了,很容易就理解數位訊號啦。想開車,會了自動擋,再學手動擋,只要稍加練習就好啦。
另外, 一定要先理解,先理解,先理解!!!
對於學生,只有理解了,才能記得住公式。否則就是背天書。
對於工程師,只有理解了,才能知道怎麽去用工具設計,怎麽去套用,而不是囫圇吞棗,照貓畫虎。
至於學習的順序,我建議如下,順帶簡單的講一下怎麽去理解,畢竟篇幅有限,只能點到為止:
1.理解什麽是正余弦訊號
正余弦訊號相當於是數位訊號處理裏面的 0 和 1,幾乎一切訊號都可以用正余弦訊號表示,也就是我們的傅立葉變換。相當於是盤古開天,從混沌到有0和1.
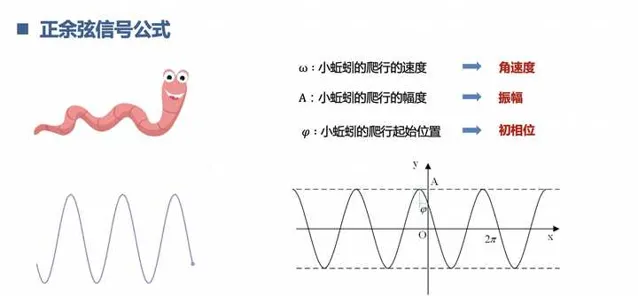
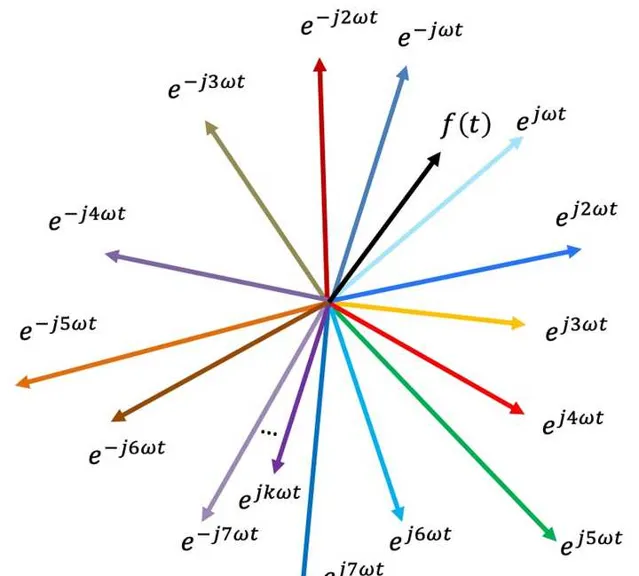
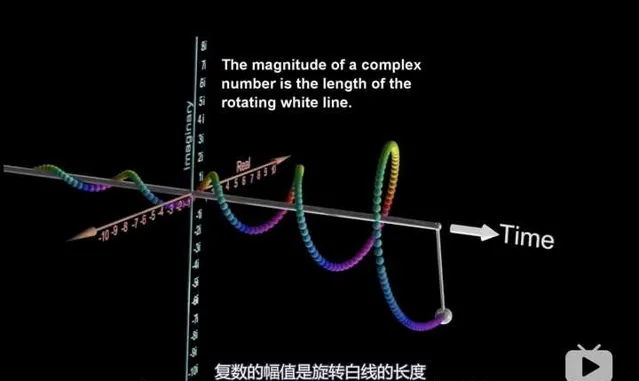
正余弦訊號也可以有更高級的玩法,透過歐拉公式可以用旋轉向量和複指數去表示正余弦訊號。你看它又寬又長,像不像衛生紙。


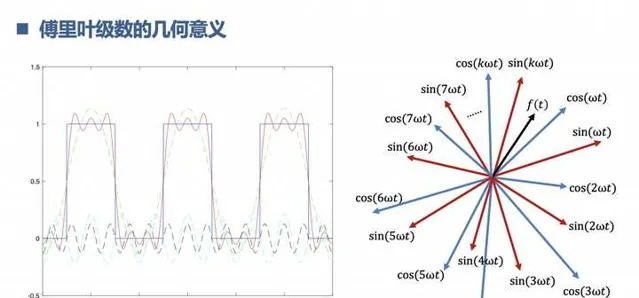
2.理解什麽是傅立葉變換
先從連續周期訊號的傅立葉級數開始,再到非周期訊號的傅立葉變換。這個時候你就懂得的,訊號世界的構成原理,幾乎所有訊號都能用正余弦訊號表示,也可以根據歐拉公式寫成複指數的形式。相當於是女媧造人,知道了復雜訊號是怎麽來的,可以怎麽拆解。同時,透過傅立葉變換,我們知道訊號的世界是兩個平行空間,一個是時間界,一個頻率界。
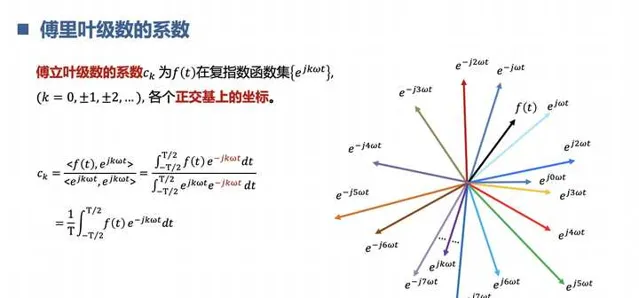
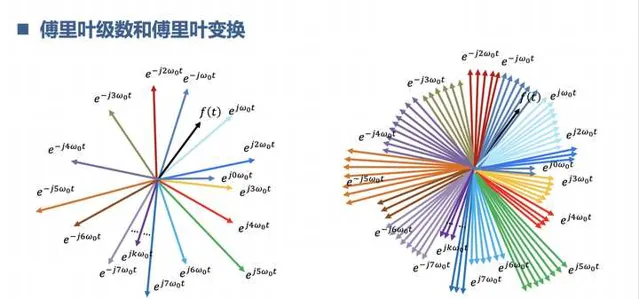
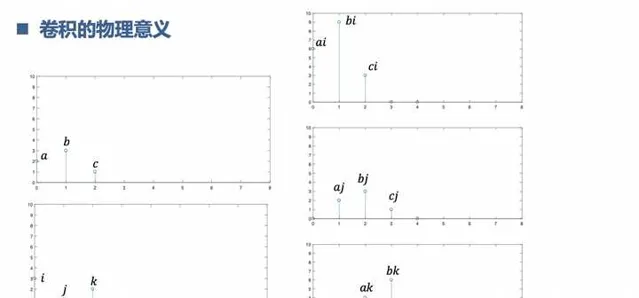
3.理解什麽是摺積
連續訊號的摺積,離散序列的摺積。這個是為後面的系統分析埋下伏筆。摺積相當於是兩個訊號的捲動摩擦(你懂的),會有新的訊號誕生。在時間界摺積,相當於頻率界乘積。在頻率界摺積,相當於時間界乘積。

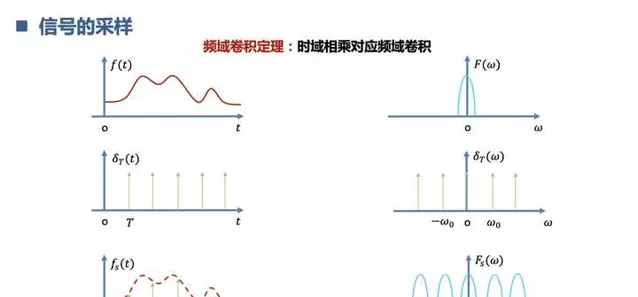
4.理解什麽是訊號采樣
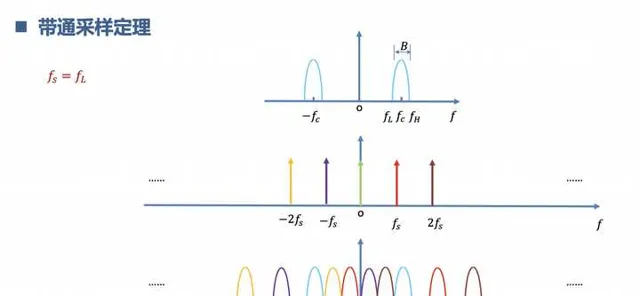
連續訊號經過采樣變為離散訊號,采樣的過程其實就是 連續訊號和 離散的沖擊脈沖相乘,時域相乘頻域摺積。相當於是從遠古時代前進演化到現代文明。用到的科技有:低通取樣定理,帶通取樣定理。
5.理解訊號的變頻
這部份書上介紹的少,實際用的多。訊號從低頻如何變到高頻? 低頻訊號乘以一個高頻的載波,時域相乘頻域摺積,訊號就卷到高頻啦,相當於是訊號們放衛星 ️,一級一級的火箭助推,最後上天。反之亦然。
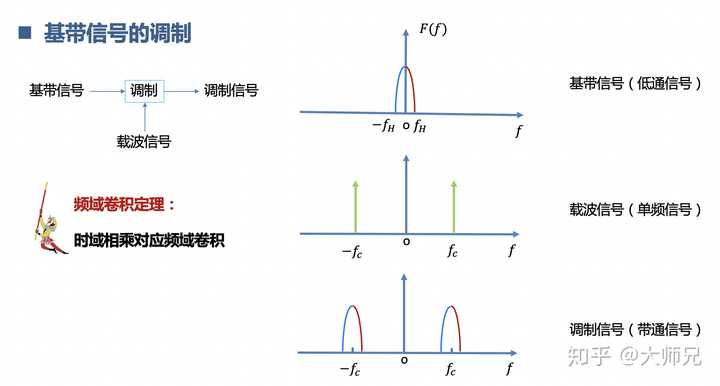
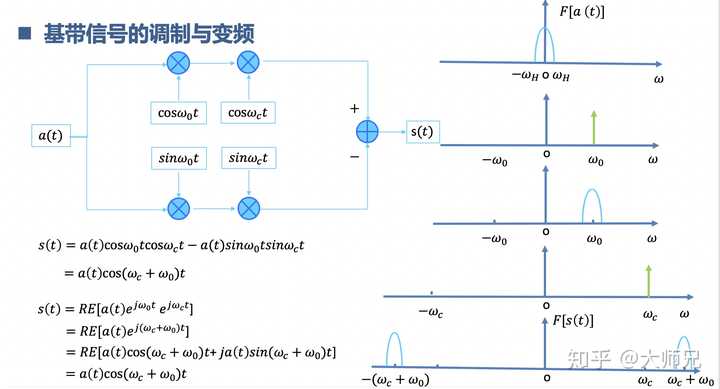
6.理解訊號的插值與抽取
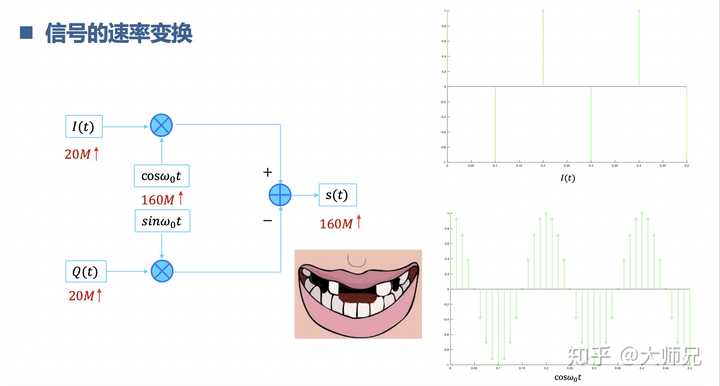
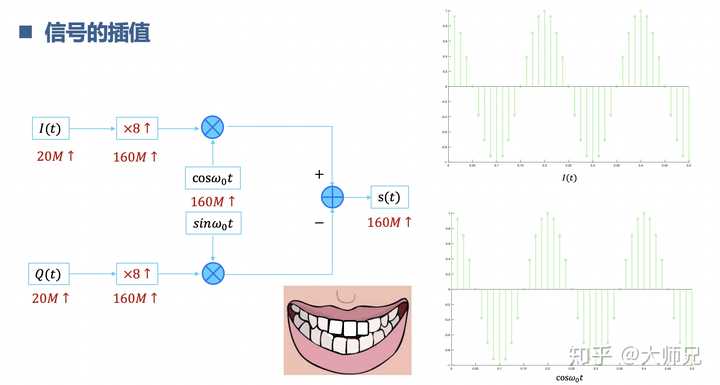
插值與抽取,也就是訊號的多速率變換。以插值為例,10M的訊號采樣速率是20M。載波的頻率是80M,采樣速率是160M。采樣速率是20M的訊號怎麽和采樣速率是160M訊號相乘。先把采樣速率是20M的訊號插值變成160M采樣速率就可以啦。相當於是掉牙了,上下牙不合,現在透過種牙補牙對齊啦,吃嘛嘛香,胃口倍棒,也有力氣學習啦。
7.理解離散傅立葉變換
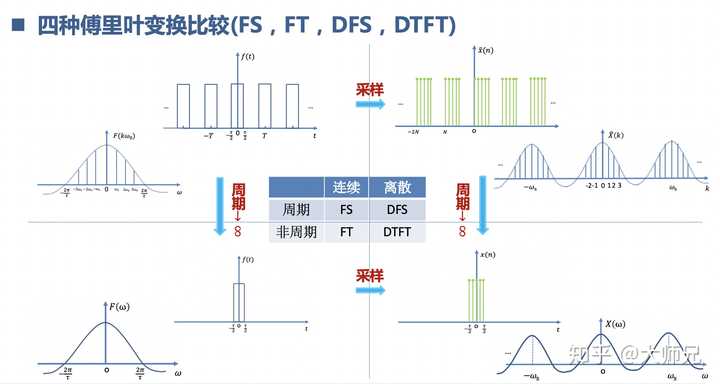
離散傅立葉變換包括: 離散時間傅立葉級數DFS,離散時間傅立葉變換DTFT,離散傅立葉變換DFT,再加上前面的 傅立葉級數FS,傅立葉變換FT。這幾個兄弟相聚啦。要好好區分一下,繞來繞去其實就是用的取樣定理的知識,時域采樣,相當於時域相乘,頻域摺積。頻域采樣,相當於頻域相乘,時域摺積。
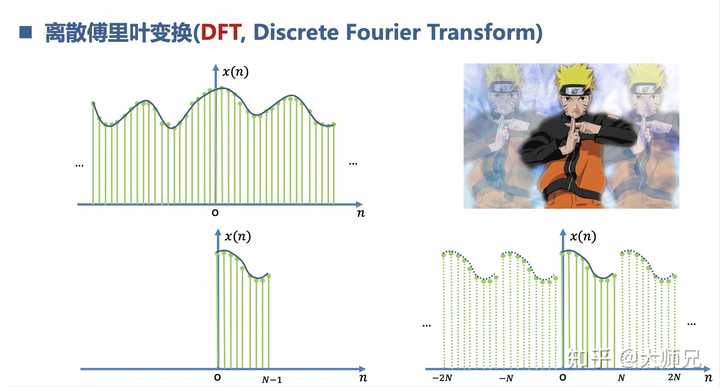
離散傅立葉變換DFT是把原本是周期的DFS截取了一個周期,因為我們的電腦記憶體裝不下一個無窮長的訊號。
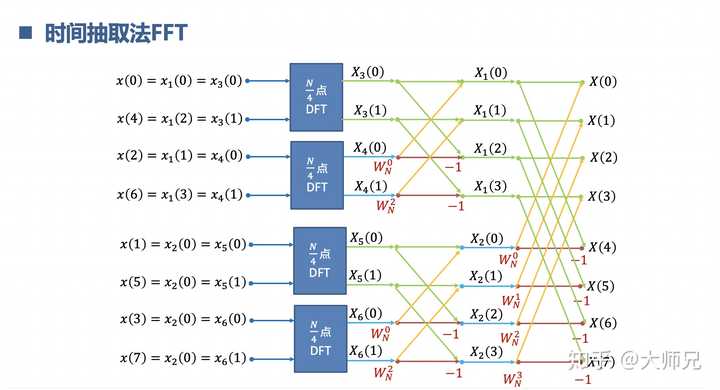
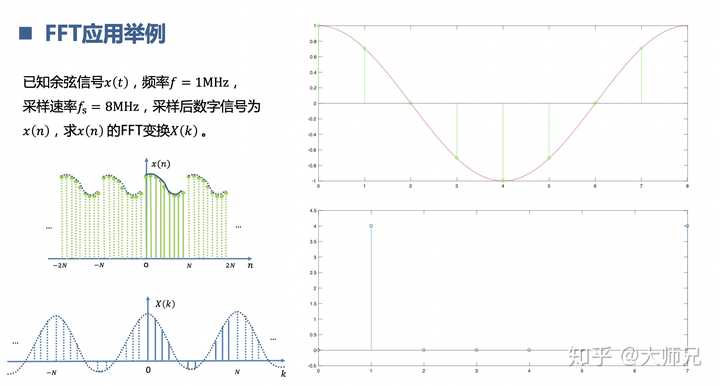
8.理解快速傅立葉變換FFT
實際工程中為了提高速度,減少資源,把DFT的演算法做了最佳化,變成了FFT。N的FFT相當於是把采樣頻率平均分成了幾份,每個點代表1/N。FFT相當於DFT是踩上筋鬥雲,一個跟頭十萬八千裏。

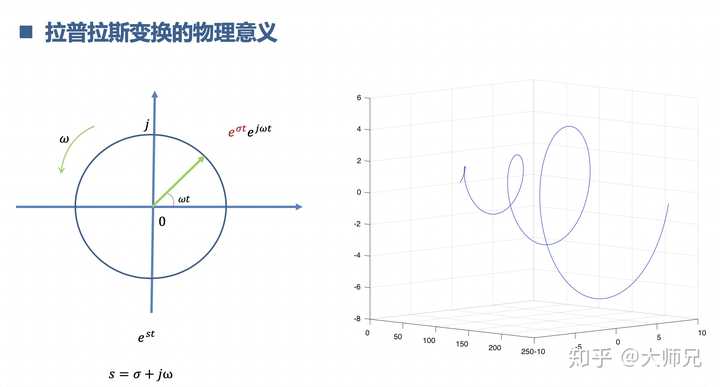
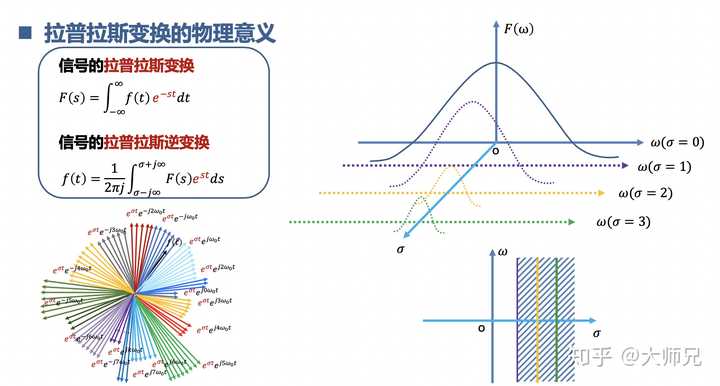
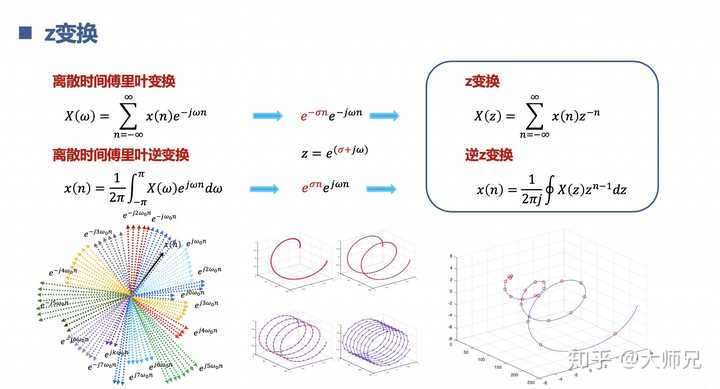
9.理解拉普拉斯變換 與z變換
拉普拉斯變換是把一些不能進行傅立葉變換的訊號先戴個金箍,念個緊箍咒,等馴服了,再傅立葉變換。z變換是拉普拉斯變換的離散數位化,z變換用來分析離散系統。相當於是社會的大躍進,沒有條件,創造條件也要上。

10.理解什麽是數位濾波器
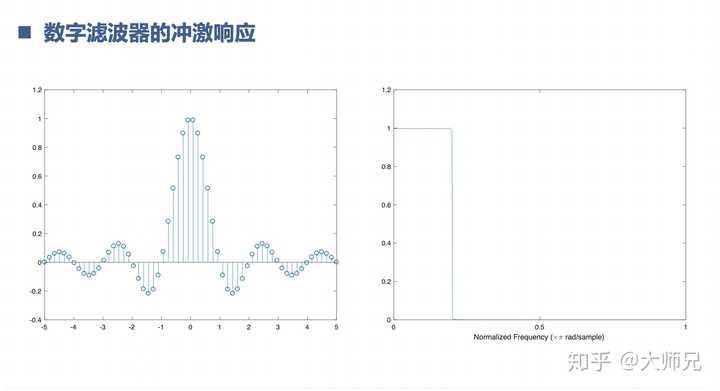
數位濾波器是以上知識的綜合運用,什麽沖激響應,取樣定理,插值抽取,傅立葉變換,摺積定理,系統函式,z變換,一個都不少。濾波器是把想要的訊號留下,不想要的訊號濾除。這就像捕魚一樣。濾波器的頻域對應系統的頻率響應,濾波器的時域對應系統的沖擊響應,這裏我們可以用z變換去分析濾波的效能。訊號經過濾波器從時域看是摺積的過程,從頻域看是相乘的過程。這裏又用到了摺積定理, 摺積定理簡直是真香定理。
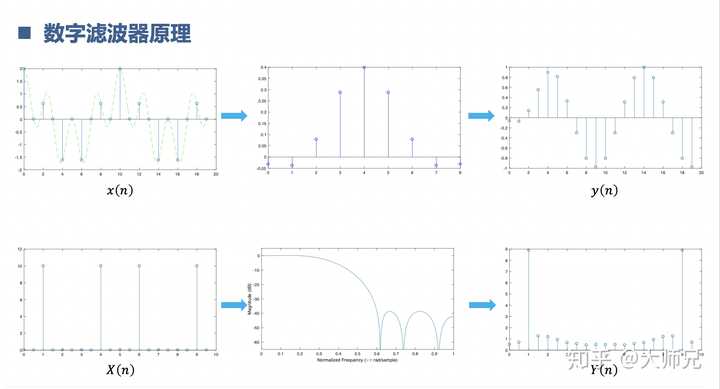
一個訊號從出生,到經歷磨難被采樣,變成數位訊號。完成了插值,相當於等牙長齊,長大成人。獲得了其他訊號的鼎力相助,也就是相乘,飛到了更高的地方,最後經過了濾波器這道凱旋門,找到了最終的歸宿,這就是訊號的一生!
我們的一生又何曾不是這樣呢?

<完>










