Sigma-Delta ADC。
這是成功將方法論擴充套件的一個典型例子。
一般的ADC模數轉換器,比如Flash,Pipeline,SAR(Successive approximation converter)等等,其原理都是直接測量。
簡單的比方吧!測量長度。
比如你面前有一根繩子,你不知道它的長度,那麽最簡單的方法,就是拿一把有精確標註的尺子來量。接著,你會發現,這把尺子必須要滿足一些條件才可以讓你成功。比如,這把尺子必須比你要量的繩子長度長(Input range之內),而且,比如你需要測量繩子長度值精確到mm,你這把尺子也需要這樣 精確的標尺 。一把精確到cm的尺子對於你來說是不合要求的。……說到這裏,大家應該可以清楚的發現,這就是最基本的Flash ADC.

接著,你可能會想,要是我的尺子沒有那麽精確的刻度,我能測量到mm量級嗎?
繼續舉例子:
繩子的長度不知道(大概是0.7m吧!)我只有一把1m長的尺子。而且呢,有個特別的地方,就是這是一把軟尺:
因此,這把 尺子是可以折疊的 。

好了,我們用這把尺子開始測量一段不知道長度的繩子。
首先,我們先把尺子對折,我們就得到了0.5m的精確量度。拿這個0.5m的尺子去跟繩子比較。好了,現在發現繩子比0.5m要長,我們就在繩子的0.5m處做個記號(或是記做1)。這時候,我們有兩種選擇:
1. 繼續折疊尺子,我們可以得到0.25m長的精確長度。然後拿0.25m長的尺子和剩下來的繩子(原長減去0.5m,比如0.7m的繩子還剩下0.2m)做比較,我們發現0.25m的尺子比剩下來的繩子長(記做0)。然後繼續對折尺子,得到0.125m。用0.125m去跟繩子比較,發現0.125m比繩子短(記做0),那麽在繩子的0.125m(也就是0.625m處)做個記號。……不斷的重復這個過程。最後的結果,就是0.5*1+0.25*0+0.125*1+……
這也就是所謂的SAR ADC。 Input不變,不斷改變reference的測量方法 。
2. 我們還可以不改變reference,也就是一直拿繩子跟0.5m做比較。0.7m長的繩子,第一次比較之後,還剩下0.2m。然後,我們把這個residue放大一倍,也就是Pipeline ADC裏面的精確乘二電路。繩子乘二的辦法,可以人為的從旁邊的繩子上截取一截一樣長的,或者任何別的方法。接著,拿放大過的0.4m跟0.5m的reference比較,發現沒有0.5m長(記做0)。然後再接著放大……一直重復。最後的結果,跟上面的結果一樣,0.5*1+0.25*0+0.125*1+……
這就是所謂的Pipeline ADC,或者是Subranging ADC, 不改變reference,只對input進行處理。
至於Integrating ADC,差不多就是拿個1cm的尺子,然後反復在繩子上一段段的標記,最後得到的精度,肯定也是1cm。
說了這麽多,其實還是為了解釋Sigma-Delta。別人都是直截了當的給出結果,Sigma-Delta卻不是這樣的。它是一種方法論上的創新。
這裏我沒法再繼續用長度了……抱歉,我需要測量一塊石頭的重量。前面的尺子全部改成天平的砝碼就好,大家就當做課外作業了哈!^_^
Sigma-Delta就是一片幽靜的封閉的池塘(Feedback Loop),然後你隨手就把石頭扔到池塘裏面去了……
隨著「噗通」一聲,石頭掉進池塘,水面上自然而然會出現對應的漣漪。一塊一百斤的石頭,和一塊一斤重的石頭,呈現出來的波紋明顯不一樣。

大石頭濺起了一米高的水花,過了好久,水花才逐漸消散。
小石頭產生的水花只有一點點,很快就被池塘的「 內力 」平息了。
一定時間內,水花濺起的高度的平均值,就是能夠用來間接測量石頭重量的關鍵數值。比如,我們已知50斤的石頭可以濺起0.5m高的水花,那麽能夠濺起1m高的水花的石頭,應該就是100斤的。那麽濺起0.01m高的水花,這個石頭則是一斤重的。
上面說到的這個池塘,有幾個必要的條件:
1.池塘不能太小:池塘要是只有一個小水缸大小,那一塊大點的石頭就把它弄壞了……比如著名的司馬光先生幹過的事情……
2. 池塘相對於石頭來說不能太大。一塊小石頭扔到海裏,呵呵……
( Dead zones are a result of finite opamp gain gain in Sigma Delta Modulators. The reason that dead zones occur is because the opamp is not able to completely transfer the charge from the sampling capacitor to the integrating capacitor.
The effect of dead zones actually results in a certain "minimum" input being present at the Modulator before it can generate a LSB so as to say.)
3.池塘必須是封閉的系統。要是還有小溪跟這個池塘連著,那麽水波就會被小溪幹擾,因此,Sigma-Delta重要的一環——integration,就沒有辦法保證準確度了。
不知道大家發現沒有,為了測量平均值,我得蹲在池塘邊上守著。隨便瞟一眼還真不行!
在一個PWM(Pulse-width modulation (PWM), or pulse-duration modulation (PDM))的Sigma-Delta中,我們要以OSR(Oversampling Rate)那麽多的時間為代價,比如Flash ADC只需要一個sampling cycle (1MHz就是1us),如果OSR是128,則為了得到一個平均值,你得蹲128us才能得到一個需要的值。(這個過程是在後續的Decimation Filter裏面完成的)
以間接的觀察閉環系統對input的反應為度量標準,以時間上的犧牲換取極高的精度,這大概就是Sigma-Delta最最精妙之處了吧!
###################################
想了很久,over sampling可以用上面的解釋,就是多sample,自然得到的結果會好一些。畢竟,我們還是依然假設quantization noise是white noise。
但是,這個精妙中的精妙noise sharping,實在是很難解釋。
實在找不到可以類比的事物,我就先講故事吧!
去年我去巴塞隆納旅遊,簡直在反復被高第的天才所擊打。其中,印象最深的就是,那座宏偉的聖家堂。在沒有CAD,沒有各種復雜的計算模型可用的時代,高第是如何建造那麽高大的建築並且保證建築符合重力學原理呢?

秘訣在於上面的「懸鏈模型」。
「上圖即為高第的聖家族大教堂懸鏈拱模型, 按照支座情況、近似模擬矢高條件做一個懸鏈模型,倒掛在天花板上。 在地板上放一面鏡子,鏡子裏看到的,就是大教堂的最佳拱軸線,也就是大教堂的結構合理造型 。壯麗無比的聖家族大教堂,竟然是用這種巧妙的方式做的結構概念設計,讓人禁不住要說一聲 Eureka!(作者:豬小寶 連結:
橋梁是不是都是凸起,而沒有凹下去的? - 豬小寶的回答)」
東扯西拉這麽多,我只是想告訴大家:有時候,把某個熟悉的東西倒過來,常常可以得到令人意想不到的奇妙。

藍色的線,是大家熟悉的opamp的TF, 紅色的線,就是把藍色的線相對x軸mirror過來的。
如果仔細看看sigma-delta:
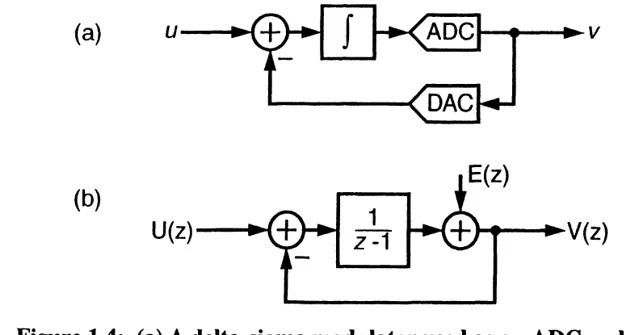
source: 「Understanding Delta-Sigma Data Converters「, Richard Schreier, Gabor C. Temes, John Wiley & Sons, 2005.
所以,很容易得到幾個傳輸函式(下圖裏,integrator是理想的):
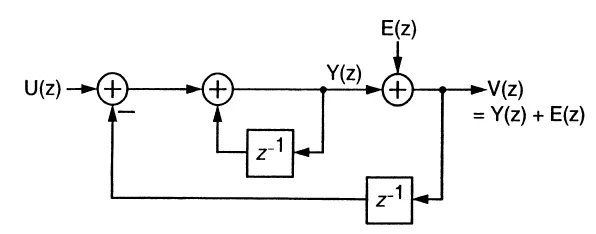

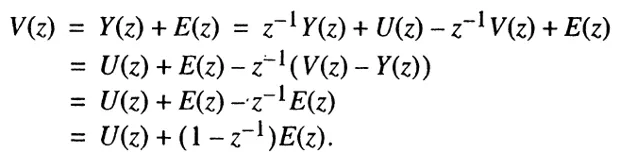
輸出基本上包含了所有的input,還有一部份的noise。如果前後兩個周期的noise相等,E(z)這一項就可以無限趨近於0了。
或者,我們不要這麽復雜的公式,把情況簡化再簡化。比如,就假設loop gain是A(s)好了,根據feedback loop的公式,從input到output,close loop transfer function便是:
H(s)=\frac{A(s)}{1-A(s)}
(參考作者的這篇講feedback之buffer的:)
對於quantization noise,loop gain是一樣的,唯一的區別,就是它的feed-forward 變成了1,而A(s)其實就是它的F(s).
H(s)=\frac{1}{1-A(s)}
因此,一個很大很大的A(s),對於noise的抑制作用,真的是非常顯著的。
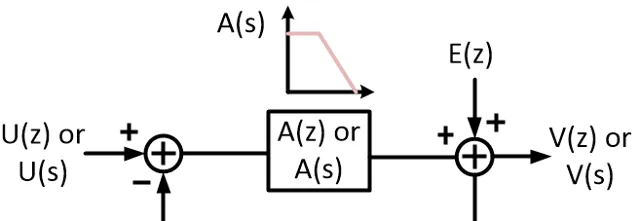
不過,這個世界上,哪有什麽理想的integrator呢?integrator裏面的opamp,肯定是有著一定的gain的。
考慮finite gain,則有leaky integrator:p=1-1/A, NTF(s)=1-pz^(-1)=1-(1-1/A)z^(-1)=(1-A(1-z))/(Az).註意,A在分母,A越大,就是opamp越理想,NTF越趨近於理想的1-z^(-1)











