怎麽證明單擺周期公式？

謝邀.

與下面的答主同為高中生. 很高興看到和本人一樣喜歡物理理論的學弟！接下來就推一下單擺周期公式.

推導這個公式本質上是建立微分方程式並求解. 這裏有兩種方法列出微分方程式：

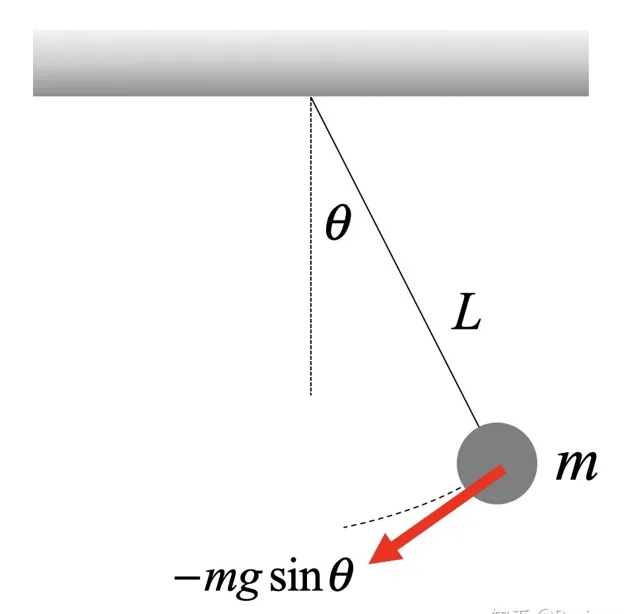
1.牛頓第二定律： 透過把重力沿著拉力方向和運動軌跡的切線方向分解，得到單擺受到的合力為 -mgsin\theta . 根據牛頓第二定律有 \(m L \frac{d^{2} \theta}{d t^{2}}=-m g \sin \theta\) , 所以微分方程式為 \(\frac{d^{2} \theta}{d t^{2}}=-\frac{g}{L} \sin \theta\) .

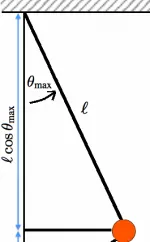
2.能量守恒定律 ：假設沒有空氣阻力，那麽動能和勢能之和應該是守恒的. 假設在某一個時刻小球離地面的高度為 h ,此時細繩與豎直方向的夾角為 \theta ，那麽小球的重力勢能應該是 mgl(1-cos\theta) ,動能應該是 \frac{1}{2}mv^2=\frac{1}{2}m(l\frac{d\theta}{dt})^2=\frac{1}{2}ml^2(\frac{d\theta}{dt})^2 . 能量總和就應該是 E=mgl(1-cos\theta)+\frac{1}{2}ml^2(\frac{d\theta}{dt})^2 . 由於能量守恒，所以 \frac{dE}{dt}=0 , 即 mglsin\theta(\frac{d\theta}{dt})+ml^2\frac{d^2\theta}{dt^2} . 最後得到的也是 \(\frac{d^{2} \theta}{d t^{2}}=-\frac{g}{l} \sin \theta\) .

現在得到了\(\frac{d^{2} \theta}{d t^{2}}=-\frac{g}{l} \sin \theta\) 這個公式，可以做一波近似，前面的答主已經說的很好了. 這裏來推導一下不做近似的公式，需要一點技巧.

\(\frac{d^{2} \theta}{d t^{2}}=\frac{d}{d t} \frac{d \theta}{d t}=\frac{d \omega}{d t}=\frac{d \omega}{d \theta} \frac{d \theta}{d t}=\omega \frac{d \omega}{d \theta}\)

於是這個方程式現在就變成了 \omega\frac{d\omega}{d\theta}=-\frac{g}{l}sin\theta . 立刻看出這個式子是可以分離變量的. 於是分離變量並且等式兩邊積分後得到 \(\omega=\sqrt{\frac{2 g}{L}\left(\cos \theta-\cos \theta_{0}\right)}=\sqrt{\frac{4 g}{L}\left(\sin ^{2} \frac{\theta_{0}}{2}-\sin ^{2} \frac{\theta}{2}\right)}\) . 其中 \theta_{0} 是初始角度.

由於 \(\int d t=\int \frac{d \theta}{\omega}\) , 得到 \(\frac{T}{4}=\int_{3 T / 4}^{T} d t=\frac{1}{2} \sqrt{\frac{L}{g}} \int_{0}^{\theta_{0}} \frac{d \theta}{\sqrt{\sin ^{2}\left(\theta_{0} / 2\right)-\sin ^{2}(\theta / 2)}}\) .

現在需要對這個積分稍微做一下變換. 令 \begin{equation} \sin \alpha=\frac{\sin (\theta / 2)}{\sin \left(\theta_{0} / 2\right)} \end{equation} , 現在關註積分的部份：

\begin{equation} \int_{0}^{\theta_{2}} \frac{d \theta}{\sqrt{\sin ^{2} \frac{\theta_{0}}{2}-\sin ^{2} \frac{\theta}{2}}}=2 \int_{0}^{\pi / 2} \frac{d \alpha}{\sqrt{1-\sin ^{2} \frac{\theta_{0}}{2} \sin ^{2} \alpha}} \end{equation} .

所以最後得到 \begin{equation} \frac{T}{4}=\sqrt{\frac{L}{g}} \int_{0}^{\pi / 2} \frac{d \alpha}{\sqrt{1-k^{2} \sin ^{2} \alpha}}, k^{2}=\sin ^{2} \frac{\theta_{0}}{2} \end{equation} .

其實到這裏已經差不多了. 這個積分叫做第一類橢圓積分，解析解是亞可比橢圓函式. 說白了就是物理學家解不出來然後就自己定義了這麽個東西. 現在到這一步硬推已經沒什麽意義了，但是如果感興趣還是可以繼續往下推導. 為了計算這個積分，需要引入以下兩個引理：

首先給出下面兩個定理作為鋪墊：

該定理被稱為廣義二項式定理. 一些人習慣記為 \[{(1 + x)^k} = \sum\limits_{n = 0}^\infty {\left( \begin{array}{l} k\\ n \end{array} \right){x^n}} \] ,不過我個人習慣用泰勒展開記憶: \[f(x) = f(0) + f'(0)x + \frac{{f''(0)}}{{2!}}{x^2} + \frac{{f'''(0)}}{{3!}}{x^3} + ...\] 之所以是廣義，就是因為此時 k 不僅僅可以是正整數，可以是任意實數.在上面的積分中，被積函式的冪 k=-\frac{1}{2} .

下面簡單證明一下這個定理. 首先設 \[u = {\sin ^{2n - 1}}x\] , \[dv = \sin xdx\] .則 \[du = (2n - 1){\sin ^{2n - 2}}x\cos xdx\] , \[v = - \cos x\] .分部積分得：

\[\int_0^{\pi /2} {{{\sin }^{2n}}xdx} = [{\sin ^{2n - 1}}x( - \cos x)]_0^{\pi /2} - \int_0^{\pi /2} {(2n - 1){{\sin }^{2n - 2}}x\cos x( - \cos x)dx} \]

\[ = (2n - 1)\int_0^{\pi /2} {{{\sin }^{2n - 2}}x{{\cos }^2}xdx} \]

\[ = (2n - 1)[\int_0^{\pi /2} {{{\sin }^{2n - 2}}xdx - } \int_0^{\pi /2} {{{\sin }^{2n}}xdx]} \]

不妨設 \[\int_0^{\pi /2} {{{\sin }^{2n}}xdx} = I\] ，對等式整理得到 \[I = \frac{{2n - 1}}{{2n}}\int_0^{\pi /2} {{{\sin }^{2n - 2}}xdx} \]

那麽很顯然對等式右邊的積分進行相同的操作後會得出 \[\int_0^{\pi /2} {{{\sin }^{2n - 2}}xdx} = \frac{{2n - 3}}{{2n - 2}}\int_0^{\pi /2} {{{\sin }^{2n - 4}}xdx} \] ,如此一直遞迴下去後得：

\[I = \frac{{(2n - 1)(2n - 3) \cdot \cdot \cdot \cdot \cdot \cdot 5 \cdot 3}}{{(2n)(2n - 2) \cdot \cdot \cdot \cdot \cdot \cdot 6 \cdot 4}}\int_0^{\pi /2} {{{\sin }^2}xdx} \]

\[ = \frac{{(2n - 1)(2n - 3) \cdot \cdot \cdot \cdot \cdot \cdot 5 \cdot 3}}{{(2n)(2n - 2) \cdot \cdot \cdot \cdot \cdot \cdot 6 \cdot 4}}\int_0^{\pi /2} {\frac{{1 + \cos 2x}}{2}dx} \]

\[\frac{{(2n - 1)(2n - 3) \cdot \cdot \cdot \cdot \cdot \cdot 5 \cdot 3 \cdot 1}}{{(2n) \cdot (2n - 2) \cdot \cdot \cdot \cdot \cdot \cdot 6 \cdot 4 \cdot 2}}\frac{\pi }{2}\]

言歸正傳，接下來我們對被積函式進行展開，根據定理1:

\[{(1 - {k^2}{\sin ^2}x )^{ - 1/2}} = 1 - \frac{1}{2}( - {k^2}{\sin ^2}x) + \frac{{\frac{1}{2} \cdot \frac{3}{2}}}{{2!}}{( - {k^2}{\sin ^2}x)^2} - \frac{{\frac{1}{2} \cdot \frac{3}{2} \cdot \frac{5}{2}}}{{3!}}{( - {k^2}{\sin ^2}x)^3} + ....\]

\[ = 1 + (\frac{1}{2}){k^2}{\sin ^2}x + (\frac{{1 \cdot 3}}{{2 \cdot 4}}){k^4}{\sin ^4}x + (\frac{{1 \cdot 3 \cdot 5}}{{2 \cdot 4 \cdot 6}}){k^6}{\sin ^6}x...\]

對被積函式逐項積分，同時利用定理2得：

\[\int_0^{\pi /2} {\frac{{dx}}{{\sqrt {1 - {k^2}{{\sin }^2}x} }} = \frac{\pi }{2} + (\frac{1}{2})(\frac{1}{2}\frac{\pi }{2}){k^2} + (\frac{{1 \cdot 3}}{{2 \cdot 4}})(\frac{{1 \cdot 3}}{{2 \cdot 4}}\frac{\pi }{2}){k^4} + (\frac{{1 \cdot 3 \cdot 5}}{{2 \cdot 4 \cdot 6}})(\frac{{1 \cdot 3 \cdot 5}}{{2 \cdot 4 \cdot 6}}\frac{\pi }{2}){k^6} + ....} \]

\[ = \frac{\pi }{2}[1 + (\frac{{{1^2}}}{{{2^2}}}){k^2} + (\frac{{{1^2} \cdot {3^2}}}{{{2^2} \cdot {4^2}}}){k^4} + (\frac{{{1^2} \cdot {3^2} \cdot {5^2}}}{{{2^2} \cdot {4^2} \cdot {6^2}}}){k^6} + ...]\]

註意這裏將 \alpha 換成了 x ，為了和前面保持一致

故周期為

\[T = 2\pi \sqrt {\frac{L}{g}} [1 + (\frac{{{1^2}}}{{{2^2}}}){k^2} + (\frac{{{1^2} \cdot {3^2}}}{{{2^2} \cdot {4^2}}}){k^4} + (\frac{{{1^2} \cdot {3^2} \cdot {5^2}}}{{{2^2} \cdot {4^2} \cdot {6^2}}}){k^6} + ...]\]

故當 k 很小時，周期可以近似寫成 \[T = 2\pi \sqrt {\frac{L}{g}} \] . 實際上一個更好的近似是 \[T = 2\pi \sqrt {\frac{L}{g}} (1 + \frac{1}{4}{k^2})\]

這裏我們來仔細研究一下上面的無窮級數.註意到從級數的第二項開始，每一項的系數都小於 \frac{1}{4} ，所以不妨把其與下面這個等比級數比較一下：

\[1 + \sum\limits_{n = 1}^\infty {\frac{1}{4}{k^{2n}}} = 1 + \frac{{{k^2}/4}}{{1 - {k^2}}} = \frac{{4 - 3{k^2}}}{{4 - 4{k^2}}}\]

很顯然該級數大於上面的周期級數，所以我們可以進行下面的數值估計：

\[2\pi \sqrt {\frac{L}{g}} (1 + \frac{1}{4}{k^2}) \le T \le 2\pi \sqrt {\frac{L}{g}} \frac{{4 - 3{k^2}}}{{4 - 4{k^2}}}\]

說到近似，實際上物理學家得出了兩個非常著名的單擺周期近似公式：

\begin{equation} T_{B} / 4=\frac{\pi}{2}\left(1+\frac{\theta_{0}^{2}}{16}\right) \end{equation}

-白努利提出的公式，實際上就是上面推到的結果再次級數展開後得到的近似.

\begin{equation} T_{K D} / 4=\frac{\pi}{2} \frac{1}{\sqrt{\cos \left(\frac{\theta_{0}}{2}\right)}} \end{equation}

-Kidd-Fog提出的公式，以簡潔優雅著稱，精確度也是相當的高.

其實我自己也曾經想過這個問題，於是將最開始提到的微分方程式全部冪級數展開求得了一個公式，近似結果是： \begin{equation} T / 4=1.57+0.094 \theta_{0}^{2}+0.007 \theta_{0}^{4} \end{equation} . 在展開項同樣多的情況下，精確度對比如下：

如果感興趣可以檢視我的專欄：