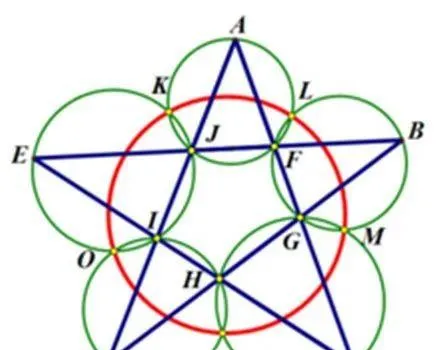
遠在2000年12月20日,江澤民主席出席澳門回歸祖國一周年慶典活動期間,在參觀濠江中學時向該校師生出了一道求證「五點共圓」的平面幾何題:「假設:任意一個星形,五個三角形,外接圓交於五點。求證:這五點共圓。」
江主席說:「我也當過中學教師,所以我對教師感到特別親切。中學教學,要教好語文、歷史、地理,數學也應該重視。」「我把這道題出給濠江中學,是要說明:一個人總要有鉆研精神。」
香港科技大學數學系副教授李健賢說,三角幾何能提供邏輯及觀察力的訓練,可鍛煉分析能力。不過,香港的數學教育註重運算,較少要求學生去處理這類幾何難題。香港只有少數大學生能解答江主席出的這道幾何題。香港喇沙中學的一名會考十優生陳貴祥表示,老師曾講授過這道考題的基本理論,但他並未做過與這道考題相關的習作。
據說,數學大師丘成桐也用了半小時才悟出此難題答案。
2000年12月28日,澳門濠江中學師生給江主席寄出了答案。兩天後,江主席請澳門特區行政長官何厚鏵轉交了給濠江中學師生的回信。
已知與求證
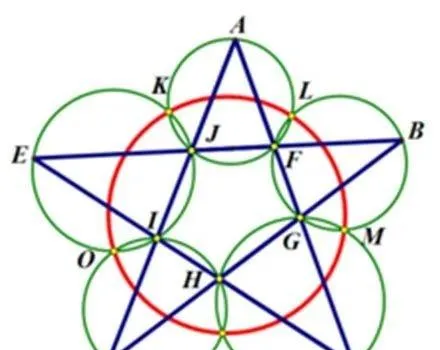
如圖,在任意五角星AJEIDHCGBF中,△AFJ、△JEI、△IDH、△HCG和△GBF各自的外接圓順次相交的交點分別是K、O、N、M、L。
求證:K、O、N、M、L五點共圓。
證明思路分析
多點共圓問題一般常見的是四點共圓,因為3點確定一個圓,4個點則是這個共圓結構需要探討的最簡形式。而一般的多點共圓問題也會轉化為多個四點共圓問題來解,即如果1234共圓,其中的3個點的組合(不妨設為123)和5共圓,那麽它們都是共的三角形123的外接圓,4和5都在三角形123的外接圓上,故5點共圓。
這雷根據五角星的射影幾何性質的C5對稱性,KLMNO五點中任意取4點的方法也是對稱的,即連續4點。且證明其共圓的方法一定和其他連續4點相同,故問題轉化為證明LMNO四點共圓(取剔除第一個字母K的代表元素)。
而證明四點共圓的一般思路,總的來說就是各種圓上邊和角相關性質定理的逆定理,大體上恰好定理的描述涉及到圓上的4個點即可。而這些定理的源頭都來源於同弧所對圓周角相等這樣的優雅性質(再往前就是三角形外角等於不相鄰內角和和因為圓的定義得到的以圓心角為頂點的一眾等腰三角形了)。由此,才有了內蝴蝶的兩個三角形翅膀的相似和相交弦定理。
當兩個點不在某線段同一側時,圓周角相等變成了內對角互補或外角等於內對角。這才有了頂點在圓外的相似三角形以及切割線定理,割線定理。
都組合起來,才有了托勒密定理,西姆松定理等。
所以本質上還是因共線構造的角和關系,因半徑相等構造的等邊三角形的底角相等為一切性質的源頭。在沒有直接的邊相關的條件和結論證據時,我們優先考慮角。
如果以KN為弦,L和M為同側頂點,證明圓周角相等,這並不是一個好思路,因為哪怕把∠KLN用相交弦LF拆開成兩個角,依然有∠FLN對著一個不知道圓上交點在哪的弧,無法進行圓上各種轉換。
LM為弦,K和N為同側頂點是類似的問題。
那就換一對不同側的,LN為弦,K和M為不同側頂點,或者對換一下,都對稱等價。總之把思路變成證明內對角互補或等價的外角等於內對角,是明確的思路。
此時∠LMN被相交弦拆為∠LMG和∠GMN,這兩個角是對稱的。反復用圓周上角的關系有:∠LMG = ∠LFA = ∠LKA,但如果兩側都用同樣的轉化,得不到什麽。
但另一側還有∠GMN = ∠GCN。兩邊一比對,發現待證明的成了∠AKN + ∠ACN = 180°的ACNK四點共圓問題。
但這依然不好證。問題依然在於,無論用哪條作參考弦,都存在不知道連出來的角和圓的交點有什麽性質。
如果說要證明5點共圓很容易轉化為4點的組合,那要證明4點共圓,想到要轉化為兩個5點,實在是太考驗幾何感覺了。
這也是平面幾何沒啥實用性,但最迷人的數學魅力。
繼續看有沒有一些角的相等轉化,全靠圓上四點結構帶來的角相等與互補關系:
∠ACN = ∠NHD = ∠NID,這就能得到ACNI四點共圓了,而這裏只有I不是ACNK中的點。
但它竟然是這個結構中的一個對稱不動點,也就是輕易的也有ACKI四點共圓。
於是得出ACNK四點共圓,原命題得證。
以上是我的思路分析,刪減一下就是分析法解答了,正向的證明也參考如下。
證明:
連線CN、HN、KN、IN、MN、MG、ML、LF、LK、KA
∵∠ACN+∠AIN=∠NHD+∠AIN=∠NID+∠AIN=180° ∴A、I、N、C四點共圓
同理A、K、I、C四點共圓從而A、C、N、K四點共圓
∴∠GMN=∠GCN=∠ACN=180°-∠AKN又∠LMG=180°-∠LFG=∠LFA=∠LKA
∴∠LMN=∠LMG+∠GMN=∠LKA+(180°-∠AKN)
∴∠LMN+∠LKN=∠LKA+(180°-∠AKN)+∠LKN=180° 故K、L、M、N四點共圓
同理可證O、L、M、N四點共圓
∴K、O、N、M、L五點共圓
證畢。
謹以此文,聊表敬意。











