我先放一個可能有點顛覆認知的東西,如下圖。

這是我某次實驗中的一杯廢液,可以看出有三層,但都是水溶液,具體成分就不說了,因為涉及到我尚未完成的課題(不回去翻實驗記錄的話我也想不起來)。簡單測了幾次密度,如果我的操作無誤的話,第一層(黃綠色)的密度比第二層(藍色,略有混濁)大 20\ mg/mL 左右。這個狀態並非解釋不了:第一層和第二層間的液面是下凹的,而下凹液面的合張力方向向上,可以把上層液體「托住」。當然這個狀態也非常不穩定:如果靜置的話應該可以維持三天以上,第三天我稍微振蕩了一下,界面迅速瓦解,三層合而為一,然後被我倒了。
下面從一個不太微觀的角度討論一下題主的問題。假設往液體B裏扔液體A的小液珠,半徑 R ,界面以上、以下部份的高度分別為 h_1、h_2 ;A和B互不相溶,密度 \rho_A、\rho_B ,A和空氣、B和空氣、A和B之間的界面張力分別為 \gamma_A、\gamma_B、\gamma_{A-B} 。
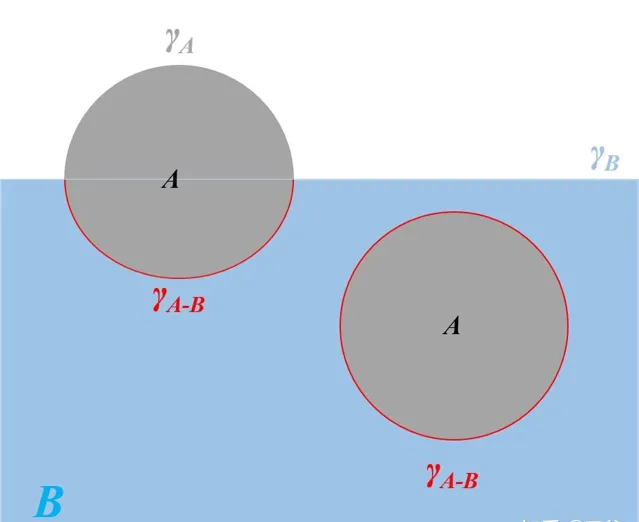
取豎直向下為正方向。假設A在B表面無法鋪展,即鋪展系數 S=\gamma_B-\gamma_A-\gamma_{A-B}<0 ;小液珠在界面上、下部份的曲率半徑分別為 R_1、R_2 ,且都是球的一部份,如果B中壓力不會引起小液珠的體積變化,那麽有這樣兩個關系
\left\{ \begin{array} +V_1+V_2=\int_{0}^{h_1}\pi\left[ R_1^2-\left( R_1-h \right)^2 \right]dh+\int_{0}^{h_2}\pi\left[ R_2^2-\left( R_2-h \right)^2 \right]dh=V=\frac{4}{3}\pi R^3\\ R_1^2-\left( R_1-h_1 \right)^2=R_2^2-\left( R_2-h_2 \right)^2 \end{array} \right. ,即
\left\{ \begin{array} \\h_1^2\left( 3R_1-h_1 \right)+h_2^2\left( 3R_2-h_2 \right)=4R^3\\ h_1\left( 2R_1-h_1 \right)=h_2(2R_2-h_2) \end{array} \right. 。
忽略界面的厚度,那麽小液珠的彎曲外表面產生的凈附加壓力 \Delta p=\gamma_A \frac{2}{R_1}-\gamma_{A-B}\frac{2}{R_2} ,那麽張力的合力
\begin{align} T &= \Delta p·S_h \\ &= \left(\gamma_A \frac{2}{R_1}-\gamma_{A-B}\frac{2}{R_2}\right)·\pi\left[ R_2^2-\left( R_2-h_2 \right)^2 \right]\\ &=\left(\gamma_A \frac{2}{R_1}-\gamma_{A-B}\frac{2}{R_2}\right)·\pi\left[ R_1^2-\left( R_1-h_1 \right)^2 \right] \end{align} ,其中 S_h 是A-B界面在水平面上的投影面積。
考慮到小液珠受到的浮力 F_f=-\rho_bgV_2=-\pi\rho_Bgh_2^2\left( R_2-\frac{1}{3}h_2 \right) 和重力 G_A=\rho_AVg=\frac{4}{3}\pi\rho_AgR^3 ,小液珠受到的淨外力 F=T+F_f+G_A 。F值為正則小液珠下沈,否則上浮或者漂浮或者懸浮。
當小液珠浸沒在B裏(右)時,顯然 T=0,h_2=2R_2=2R,F=\frac{4}{3}\pi\left(\rho_A -\rho_B \right)gR^3 ,A密度更大的話,淨外力向下,就會下沈。
對於圖中左邊的情況, F=\left(\gamma_A \frac{2}{R_1}-\gamma_{A-B}\frac{2}{R_2}\right)·\pi\left[ R_2^2-\left( R_2-h_2 \right)^2 \right]+\frac{4}{3}\pi\rho_AgR^3-\pi\rho_Bgh_2^2\left( R_2-\frac{1}{3}h_2 \right) 。第二三項主要和密度有關,先考慮 \rho_A>\rho_B ,一定有 \frac{4}{3}\pi\rho_AgR^3-\pi\rho_Bgh_2^2\left( R_2-\frac{1}{3}h_2 \right)>\frac{4}{3}\pi\left(\rho_A -\rho_B \right)gR^3>0 ,所以這種情況下小液珠更多地傾向於下沈;不過可以註意到第一項主要和界面張力有關,有個粗略的規律是界面張力越大則對應的曲率半徑越小。理論上只要 \gamma_A 足夠小或 \gamma_{A-B} 足夠大,在 \rho_A、\rho_B 差距不大,且R較小時,就可能使得F取負值,也就是讓一個密度較大的液珠飄在密度較小的液體表面。
如果 \rho_A<\rho_B 呢?那就很簡單了,即使 \gamma_A 足夠大以致於使小液珠產生了下沈的趨勢,一旦小液珠浸沒到B中就會被淨外力推回到表面上。
回到最開始放的那個廢液,黃綠色的第一層的上下表面都是下凹的,對「托起」這層液體都是有利的。振蕩之後,界面瓦解,彼此混溶,因為這三層都是水溶液(分層是因為它們的溶質濃度都不低,以致於改變了其中水的性質,或者說其中的水已經不是相同的「水」,沒那麽容易產生交互作用了,而振蕩使得水合成分之間發生碰撞、交換,這些不同的水又可以發生交互作用了)。如果是彼此不互溶的液體,比如前面舉例的A和B,如下圖,這裏不考慮容器壁的影響。
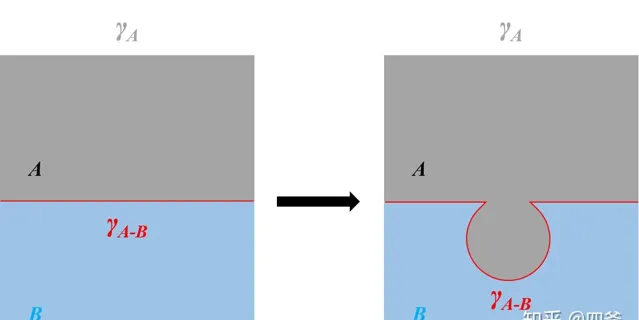
假設 \rho_A>\rho_B ,並且像左邊一樣分布,振蕩後很容易出現類似右邊的狀況:界面增大,在界面張力的作用下界面由縮回去的趨勢;同時凸出來的界面處上會受到額外的壓力,因為如果以初始界面處為壓力零點,在凸出來的界面上距初始界面深度為h的位置,由A產生的壓力為 p_A=\rho_Agh ,由B產生的壓力為 p_B=\rho_Bgh<\rho_Agh=p_A ,當界面張力不足以抵消這部份壓力差時,A就會順著這個凸出來的部份流到底下去。
如果 \rho_A<\rho_B ,形成右邊的狀態後,界面張力和凈壓力的作用是一致的,都會把凸出來的這部份懟回去。
當然,也可能出現向上凸的部份,情況基本雷同,就不贅述了。
如果要從微觀上討論這個問題的話,那就需要去分析在原子、分子層面,影響液體密度和界面張力的因素都有哪些。太復雜,足夠寫本書了,所以
略。











