无妖自来,人在花果山,刚下筋斗云。
先说结论:【数字信号处理】这门课,如果方法得当,有人指点,是可以几天学完的。
然后我们再来分析一下如何学好【数字信号处理】这门课。
【内容提要】
- 【数字信号处理】要学什么?与【信号与系统】的关系?
- 【数字信号处理】为什么难学?
- 【数字信号处理】的学习方法?
- 【数字信号处理】的学习顺序和理解?
1【数字信号处理】要学什么?与【信号与系统】的关系?
我们对比一下几本【数字信号处理】的书:




我们不难看出,其实数字信号处理主要包括:离散傅立叶变换类(DTFT,DFT,FFT),多速率数字信号处理(插值,抽取),z变换,离散时间系统分析,数字滤波器(FIR,IIR)。
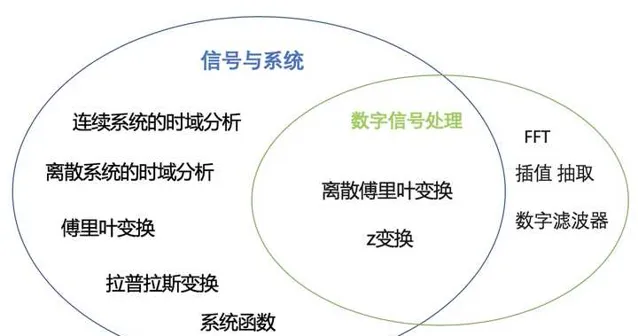
我们再来看一下 【信号与系统】与【数字信号处理】的关系,找2本对比一下:


你会发现二者有很大一部分是交叉重合的,比如 离散傅里叶变换, z变换。而【数字信号处理】比【信号与系统】多的部分基本上就是:FFT,多速率数字信号处理(插值,抽取),数字滤波器。如果我们【信号与系统】学的很好,也就是72变都会了,学【数字信号处理】相当于再学个筋斗云就够啦。
2【数字信号处理】为什么难学?
1. 我们的基础知识不够扎实
学习【数字信号处理】需要用到 【信号与系统】的知识,通过上面分析,我们知道基本上【信号与系统】包含了【数字信号处理】绝大部分知识,采样,卷积,傅立叶变换,拉普拉斯变换,Z变换,系统响应。如果我们【信号与系统】没有学好的话,那么【数字信号处理】学起来就很吃力啦。 打个比方,你开过自动挡的车,如果再去学开手动挡的车,会比只直接学开手动挡要容易很多。
除此之外,还要用到高数知识,甚至是中数(初中数学)知识。 比如:三角函数,欧拉公式,微分,积分。 这些公式相当于是对数学知识的实践应用,如果没有掌握的话,看那些数学公式和推导就会有看天书的感觉啦。

2. 教材有问题
数字信号处理是一门工程学科,但是我们的教材是偏数学,偏理论的。
我们的教材为了严谨和简洁(公式相比文字看起啦要简洁),基本上都是数学公式推导证明,所以应该叫做 【数学信号处理】 更准确一些。
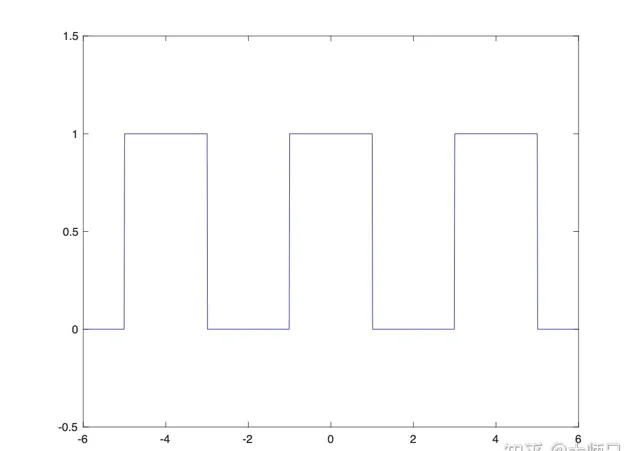
但是让你写出矩形信号的表达式和傅里叶级数,恐怕就不那么容易啦,如果再让你用矩形信号和一个其他信号做个卷积,那就更难啦。我们的教材为了到达通用性的目的,不会由浅入深的讲解。其实,可能从简单的正余弦函数开始讲起,让大家从简单的开始理解效果会更好。比如,余弦信号是怎么来的,余弦信号的频谱特性是什么。余弦信号的傅里叶变换,采样,插值,抽取,变频,滤波。

3. 老师讲的有问题
事先声明,我很尊敬老师,没有贬低的意思。只是数字信号处理是偏工程应用的科目。可能很多老师并没有实际的项目经验的。这也就造成了一个现象,老师的理论性很强,推导证明书上的公式没问题,但是很少讲公式的物理意义和定理的实际应用。
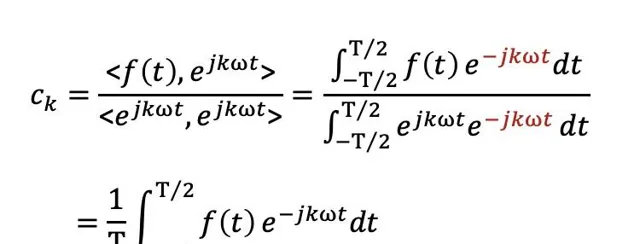
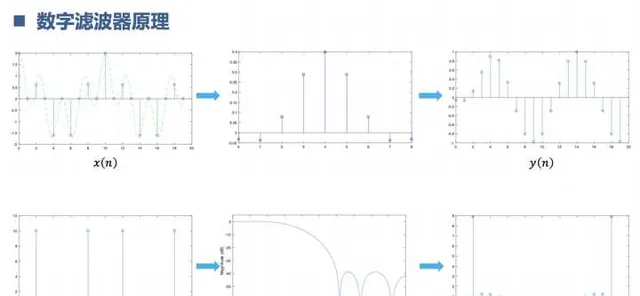
3【数字信号处理】的学习方法?
1.顺藤摸瓜
哪里不会点哪里。三角函数不会了就查一下,积分不会了也先复习一下。手边备一本【高等数学】和【信号与系统】。记住【信号与系统】几乎包含了80%的数字信号处理知识。
2.博采众长
不能只看一本书,可以看看其他版本的书。尤其是当一个地方看不明白的时候,看看其他的书是怎么讲的。很多时候,一本书有的地方模棱两可一笔带过,而另一本书讲得却比较详细。如果在学校,同时从图书馆多借几本。如果不在学校,可以从网上找找电子版的。
3.拜佛求仙
如果看了几本书,还是不懂。上网查资料,网上有很多大神能够把很难懂的知识讲的很容易理解。博客 -> 知乎-> b站 总有一款适合你。
不信你来感受一下让人拉不出屎的拉普拉斯变换。看完肯定会舒畅很多。
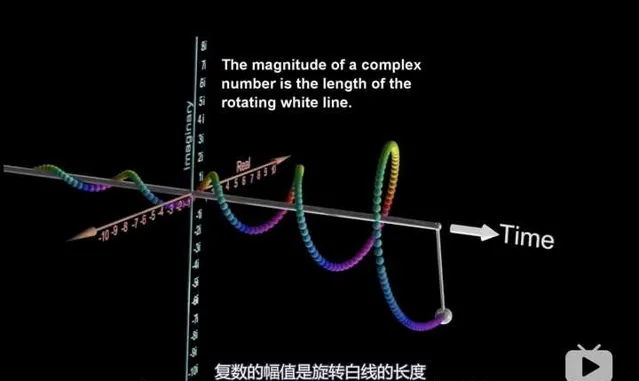
还有关系非常暧昧的三大变换。
4.破财免灾
【 白嫖 】如果你时间宝贵,书也不想看,想躺着学数字信号处理,可以试听一下大师兄的视频。
【 恰饭 】如果你家里有矿不差钱,或者少充个王者礼包,省下来可以考虑来个全套。
4【数字信号处理】的学习顺序和理解?
如果你想自己学,我建议把【信号与系统】和【数字信号处理】一起学,这样看似学的东西要多,但实际会加快我们的速度和理解程度。把连续信号学明白了,很容易就理解数字信号啦。想开车,会了自动挡,再学手动挡,只要稍加练习就好啦。
另外, 一定要先理解,先理解,先理解!!!
对于学生,只有理解了,才能记得住公式。否则就是背天书。
对于工程师,只有理解了,才能知道怎么去用工具设计,怎么去应用,而不是囫囵吞枣,照猫画虎。
至于学习的顺序,我建议如下,顺带简单的讲一下怎么去理解,毕竟篇幅有限,只能点到为止:
1.理解什么是正余弦信号
正余弦信号相当于是数字信号处理里面的 0 和 1,几乎一切信号都可以用正余弦信号表示,也就是我们的傅里叶变换。相当于是盘古开天,从混沌到有0和1.
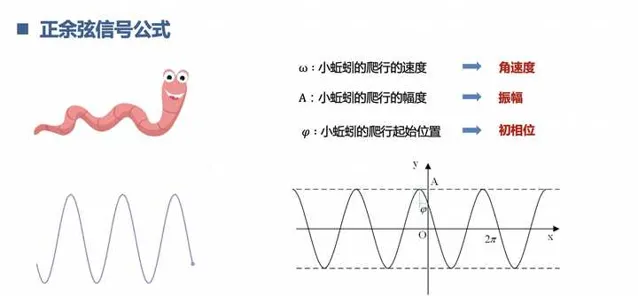
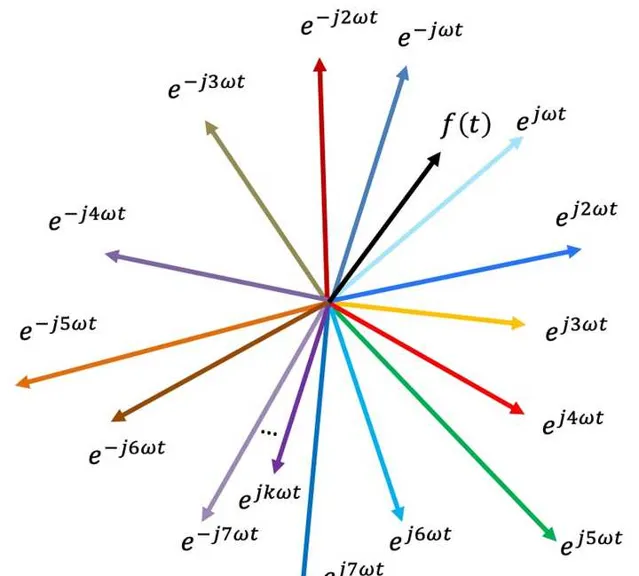
正余弦信号也可以有更高级的玩法,通过欧拉公式可以用旋转向量和复指数去表示正余弦信号。你看它又宽又长,像不像卫生纸。


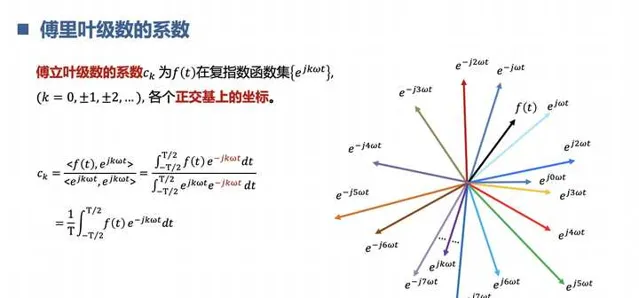
2.理解什么是傅里叶变换
先从连续周期信号的傅里叶级数开始,再到非周期信号的傅里叶变换。这个时候你就懂得的,信号世界的构成原理,几乎所有信号都能用正余弦信号表示,也可以根据欧拉公式写成复指数的形式。相当于是女娲造人,知道了复杂信号是怎么来的,可以怎么拆解。同时,通过傅里叶变换,我们知道信号的世界是两个平行空间,一个是时间界,一个频率界。
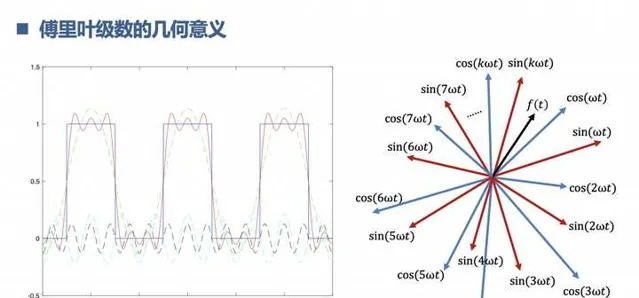
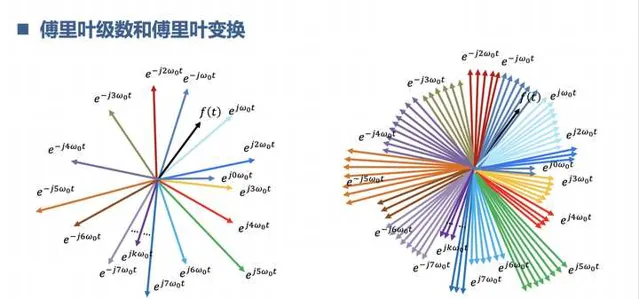
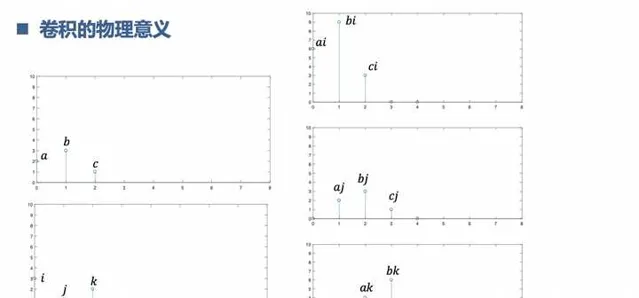
3.理解什么是卷积
连续信号的卷积,离散序列的卷积。这个是为后面的系统分析埋下伏笔。卷积相当于是两个信号的滚动摩擦(你懂的),会有新的信号诞生。在时间界卷积,相当于频率界乘积。在频率界卷积,相当于时间界乘积。

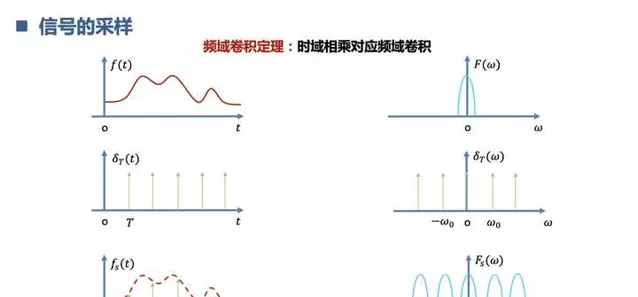
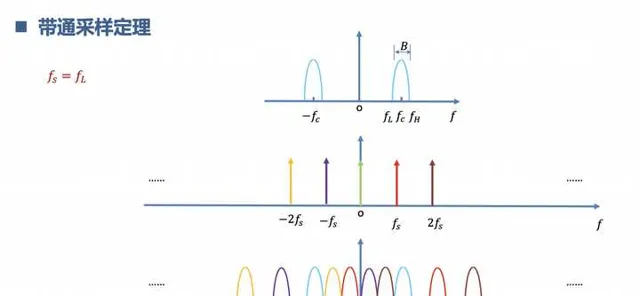
4.理解什么是信号采样
连续信号经过采样变为离散信号,采样的过程其实就是 连续信号和 离散的冲击脉冲相乘,时域相乘频域卷积。相当于是从远古时代进化到现代文明。用到的科技有:低通采样定理,带通采样定理。
5.理解信号的变频
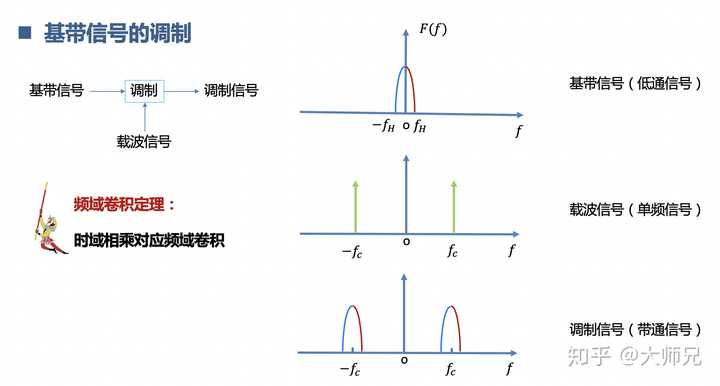
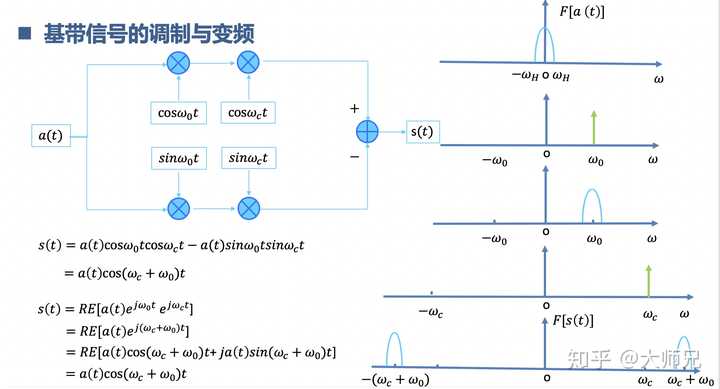
这部分书上介绍的少,实际用的多。信号从低频如何变到高频? 低频信号乘以一个高频的载波,时域相乘频域卷积,信号就卷到高频啦,相当于是信号们放卫星 ️,一级一级的火箭助推,最后上天。反之亦然。
6.理解信号的插值与抽取
插值与抽取,也就是信号的多速率变换。以插值为例,10M的信号采样速率是20M。载波的频率是80M,采样速率是160M。采样速率是20M的信号怎么和采样速率是160M信号相乘。先把采样速率是20M的信号插值变成160M采样速率就可以啦。相当于是掉牙了,上下牙不合,现在通过种牙补牙对齐啦,吃嘛嘛香,胃口倍棒,也有力气学习啦。
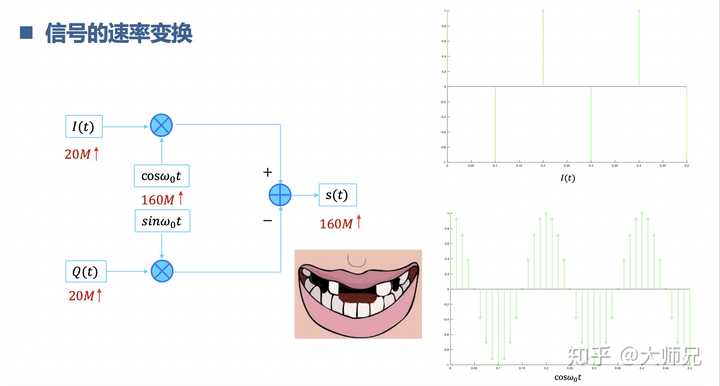
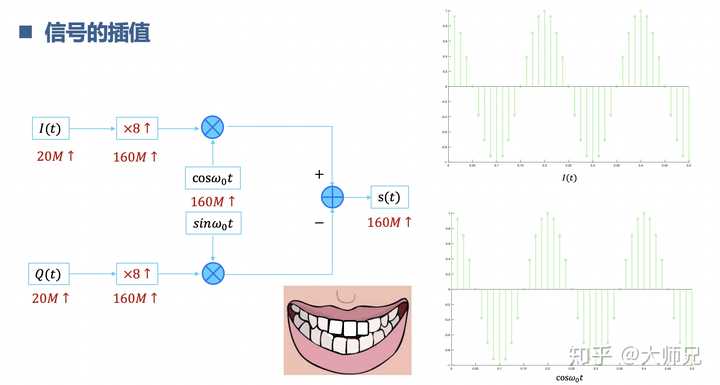
7.理解离散傅里叶变换
离散傅里叶变换包括: 离散时间傅里叶级数DFS,离散时间傅里叶变换DTFT,离散傅里叶变换DFT,再加上前面的 傅里叶级数FS,傅里叶变换FT。这几个兄弟相聚啦。要好好区分一下,绕来绕去其实就是用的采样定理的知识,时域采样,相当于时域相乘,频域卷积。频域采样,相当于频域相乘,时域卷积。
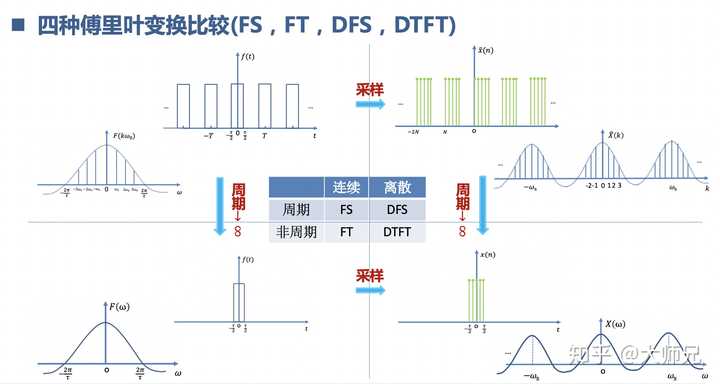
离散傅里叶变换DFT是把原本是周期的DFS截取了一个周期,因为我们的电脑内存装不下一个无穷长的信号。
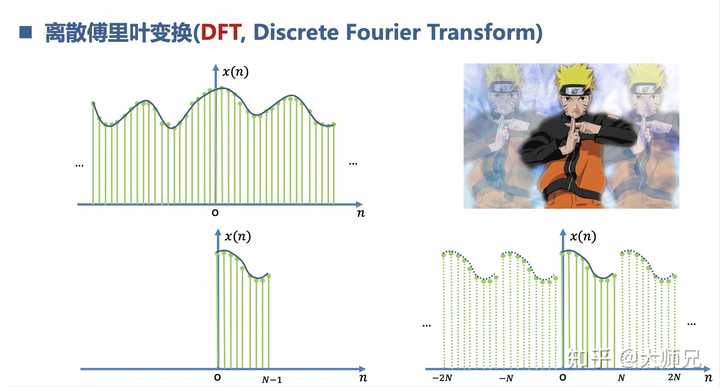
8.理解快速傅里叶变换FFT
实际工程中为了提高速度,减少资源,把DFT的算法做了优化,变成了FFT。N的FFT相当于是把采样频率平均分成了几份,每个点代表1/N。FFT相当于DFT是踩上筋斗云,一个跟头十万八千里。

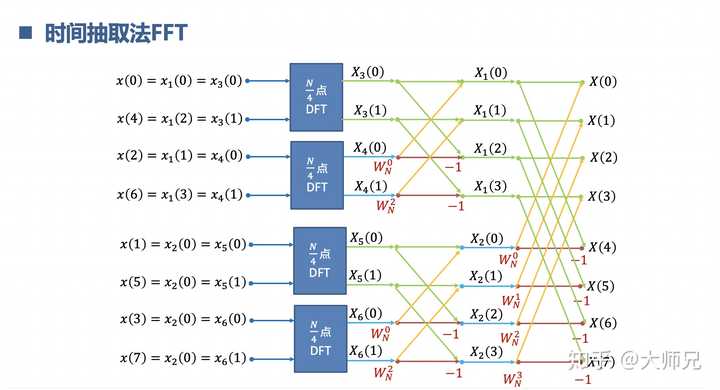
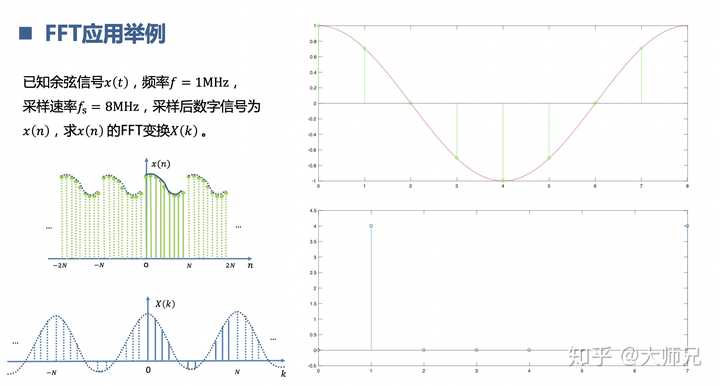
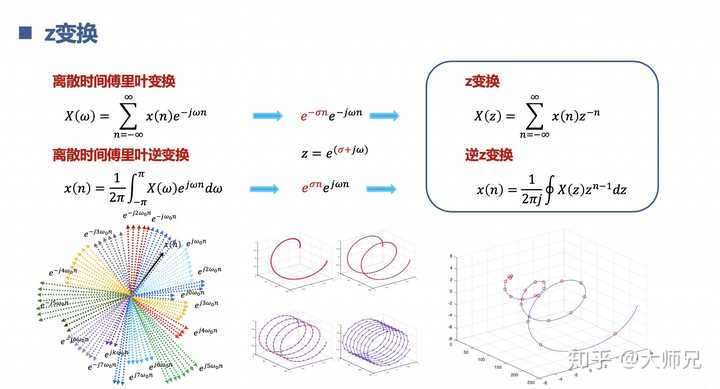
9.理解拉普拉斯变换 与z变换
拉普拉斯变换是把一些不能进行傅里叶变换的信号先戴个金箍,念个紧箍咒,等驯服了,再傅里叶变换。z变换是拉普拉斯变换的离散数字化,z变换用来分析离散系统。相当于是社会的大跃进,没有条件,创造条件也要上。

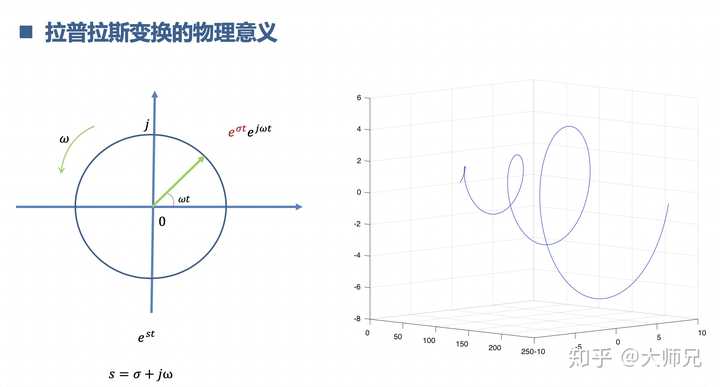
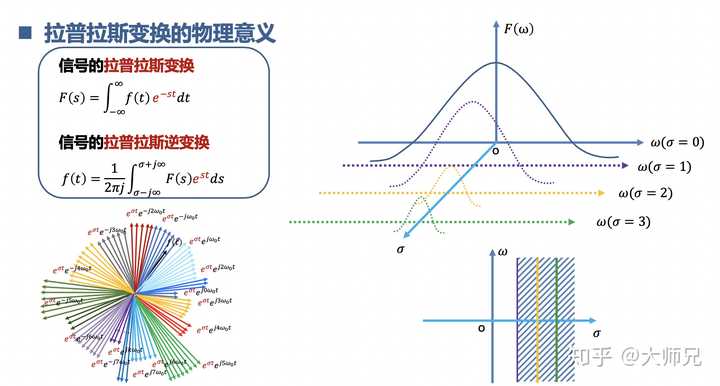
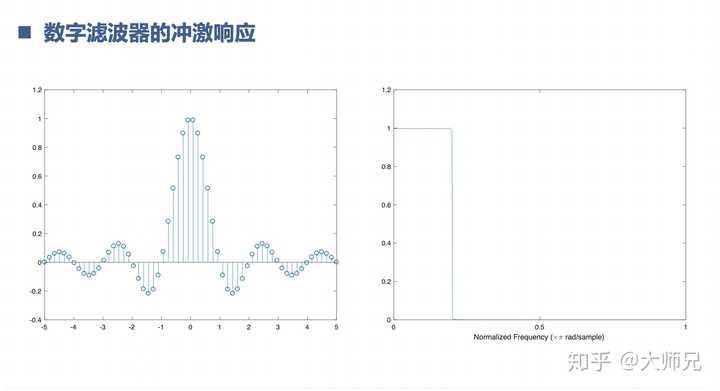
10.理解什么是数字滤波器
数字滤波器是以上知识的综合运用,什么冲激响应,采样定理,插值抽取,傅里叶变换,卷积定理,系统函数,z变换,一个都不少。滤波器是把想要的信号留下,不想要的信号滤除。这就像捕鱼一样。滤波器的频域对应系统的频率响应,滤波器的时域对应系统的冲击响应,这里我们可以用z变换去分析滤波的性能。信号经过滤波器从时域看是卷积的过程,从频域看是相乘的过程。这里又用到了卷积定理, 卷积定理简直是真香定理。
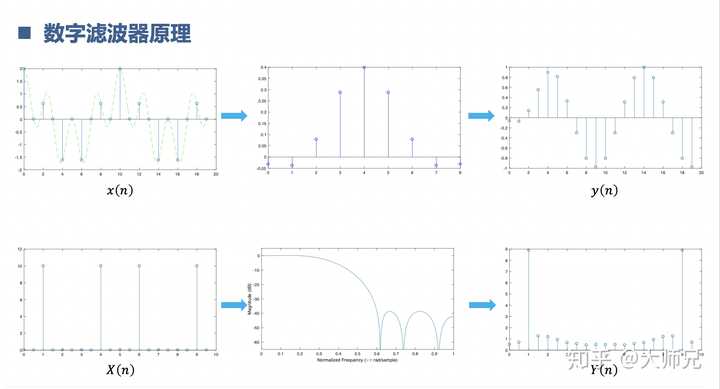
一个信号从出生,到经历磨难被采样,变成数字信号。完成了插值,相当于等牙长齐,长大成人。获得了其他信号的鼎力相助,也就是相乘,飞到了更高的地方,最后经过了滤波器这道凯旋门,找到了最终的归宿,这就是信号的一生!
我们的一生又何曾不是这样呢?

<完>










