Sigma-Delta ADC。
这是成功将方法论扩展的一个典型例子。
一般的ADC模数转换器,比如Flash,Pipeline,SAR(Successive approximation converter)等等,其原理都是直接测量。
简单的比方吧!测量长度。
比如你面前有一根绳子,你不知道它的长度,那么最简单的方法,就是拿一把有精确标注的尺子来量。接着,你会发现,这把尺子必须要满足一些条件才可以让你成功。比如,这把尺子必须比你要量的绳子长度长(Input range之内),而且,比如你需要测量绳子长度值精确到mm,你这把尺子也需要这样 精确的标尺 。一把精确到cm的尺子对于你来说是不合要求的。……说到这里,大家应该可以清楚的发现,这就是最基本的Flash ADC.

接着,你可能会想,要是我的尺子没有那么精确的刻度,我能测量到mm量级吗?
继续举例子:
绳子的长度不知道(大概是0.7m吧!)我只有一把1m长的尺子。而且呢,有个特别的地方,就是这是一把软尺:
因此,这把 尺子是可以折叠的 。

好了,我们用这把尺子开始测量一段不知道长度的绳子。
首先,我们先把尺子对折,我们就得到了0.5m的精确量度。拿这个0.5m的尺子去跟绳子比较。好了,现在发现绳子比0.5m要长,我们就在绳子的0.5m处做个记号(或是记做1)。这时候,我们有两种选择:
1. 继续折叠尺子,我们可以得到0.25m长的精确长度。然后拿0.25m长的尺子和剩下来的绳子(原长减去0.5m,比如0.7m的绳子还剩下0.2m)做比较,我们发现0.25m的尺子比剩下来的绳子长(记做0)。然后继续对折尺子,得到0.125m。用0.125m去跟绳子比较,发现0.125m比绳子短(记做0),那么在绳子的0.125m(也就是0.625m处)做个记号。……不断的重复这个过程。最后的结果,就是0.5*1+0.25*0+0.125*1+……
这也就是所谓的SAR ADC。 Input不变,不断改变reference的测量方法 。
2. 我们还可以不改变reference,也就是一直拿绳子跟0.5m做比较。0.7m长的绳子,第一次比较之后,还剩下0.2m。然后,我们把这个residue放大一倍,也就是Pipeline ADC里面的精确乘二电路。绳子乘二的办法,可以人为的从旁边的绳子上截取一截一样长的,或者任何别的方法。接着,拿放大过的0.4m跟0.5m的reference比较,发现没有0.5m长(记做0)。然后再接着放大……一直重复。最后的结果,跟上面的结果一样,0.5*1+0.25*0+0.125*1+……
这就是所谓的Pipeline ADC,或者是Subranging ADC, 不改变reference,只对input进行处理。
至于Integrating ADC,差不多就是拿个1cm的尺子,然后反复在绳子上一段段的标记,最后得到的精度,肯定也是1cm。
说了这么多,其实还是为了解释Sigma-Delta。别人都是直截了当的给出结果,Sigma-Delta却不是这样的。它是一种方法论上的创新。
这里我没法再继续用长度了……抱歉,我需要测量一块石头的重量。前面的尺子全部改成天平的砝码就好,大家就当做课外作业了哈!^_^
Sigma-Delta就是一片幽静的封闭的池塘(Feedback Loop),然后你随手就把石头扔到池塘里面去了……
随着「噗通」一声,石头掉进池塘,水面上自然而然会出现对应的涟漪。一块一百斤的石头,和一块一斤重的石头,呈现出来的波纹明显不一样。

大石头溅起了一米高的水花,过了好久,水花才逐渐消散。
小石头产生的水花只有一点点,很快就被池塘的「 内力 」平息了。
一定时间内,水花溅起的高度的平均值,就是能够用来间接测量石头重量的关键数值。比如,我们已知50斤的石头可以溅起0.5m高的水花,那么能够溅起1m高的水花的石头,应该就是100斤的。那么溅起0.01m高的水花,这个石头则是一斤重的。
上面说到的这个池塘,有几个必要的条件:
1.池塘不能太小:池塘要是只有一个小水缸大小,那一块大点的石头就把它弄坏了……比如著名的司马光先生干过的事情……
2. 池塘相对于石头来说不能太大。一块小石头扔到海里,呵呵……
( Dead zones are a result of finite opamp gain gain in Sigma Delta Modulators. The reason that dead zones occur is because the opamp is not able to completely transfer the charge from the sampling capacitor to the integrating capacitor.
The effect of dead zones actually results in a certain "minimum" input being present at the Modulator before it can generate a LSB so as to say.)
3.池塘必须是封闭的系统。要是还有小溪跟这个池塘连着,那么水波就会被小溪干扰,因此,Sigma-Delta重要的一环——integration,就没有办法保证准确度了。
不知道大家发现没有,为了测量平均值,我得蹲在池塘边上守着。随便瞟一眼还真不行!
在一个PWM(Pulse-width modulation (PWM), or pulse-duration modulation (PDM))的Sigma-Delta中,我们要以OSR(Oversampling Rate)那么多的时间为代价,比如Flash ADC只需要一个sampling cycle (1MHz就是1us),如果OSR是128,则为了得到一个平均值,你得蹲128us才能得到一个需要的值。(这个过程是在后续的Decimation Filter里面完成的)
以间接的观察闭环系统对input的反应为度量标准,以时间上的牺牲换取极高的精度,这大概就是Sigma-Delta最最精妙之处了吧!
###################################
想了很久,over sampling可以用上面的解释,就是多sample,自然得到的结果会好一些。毕竟,我们还是依然假设quantization noise是white noise。
但是,这个精妙中的精妙noise sharping,实在是很难解释。
实在找不到可以类比的事物,我就先讲故事吧!
去年我去巴塞罗那旅游,简直在反复被高迪的天才所击打。其中,印象最深的就是,那座宏伟的圣家堂。在没有CAD,没有各种复杂的计算模型可用的时代,高迪是如何建造那么高大的建筑并且保证建筑符合重力学原理呢?

秘诀在于上面的「悬链模型」。
「上图即为高迪的圣家族大教堂悬链拱模型, 按照支座情况、近似模拟矢高条件做一个悬链模型,倒挂在天花板上。 在地板上放一面镜子,镜子里看到的,就是大教堂的最佳拱轴线,也就是大教堂的结构合理造型 。壮丽无比的圣家族大教堂,竟然是用这种巧妙的方式做的结构概念设计,让人禁不住要说一声 Eureka!(作者:猪小宝 链接:
桥梁是不是都是凸起,而没有凹下去的? - 猪小宝的回答)」
东扯西拉这么多,我只是想告诉大家:有时候,把某个熟悉的东西倒过来,常常可以得到令人意想不到的奇妙。

蓝色的线,是大家熟悉的opamp的TF, 红色的线,就是把蓝色的线相对x轴mirror过来的。
如果仔细看看sigma-delta:
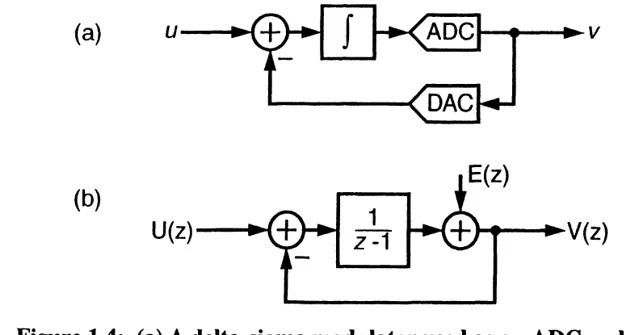
source: 「Understanding Delta-Sigma Data Converters「, Richard Schreier, Gabor C. Temes, John Wiley & Sons, 2005.
所以,很容易得到几个传输函数(下图里,integrator是理想的):
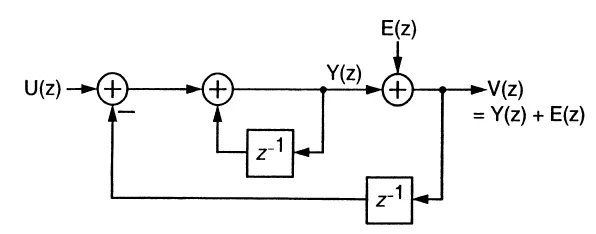

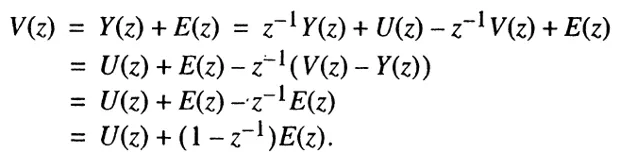
输出基本上包含了所有的input,还有一部分的noise。如果前后两个周期的noise相等,E(z)这一项就可以无限趋近于0了。
或者,我们不要这么复杂的公式,把情况简化再简化。比如,就假设loop gain是A(s)好了,根据feedback loop的公式,从input到output,close loop transfer function便是:
H(s)=\frac{A(s)}{1-A(s)}
(参考作者的这篇讲feedback之buffer的:)
对于quantization noise,loop gain是一样的,唯一的区别,就是它的feed-forward 变成了1,而A(s)其实就是它的F(s).
H(s)=\frac{1}{1-A(s)}
因此,一个很大很大的A(s),对于noise的抑制作用,真的是非常显著的。
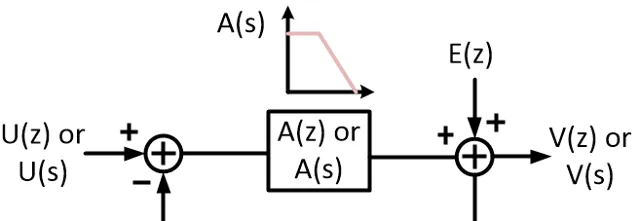
不过,这个世界上,哪有什么理想的integrator呢?integrator里面的opamp,肯定是有着一定的gain的。
考虑finite gain,则有leaky integrator:p=1-1/A, NTF(s)=1-pz^(-1)=1-(1-1/A)z^(-1)=(1-A(1-z))/(Az).注意,A在分母,A越大,就是opamp越理想,NTF越趋近于理想的1-z^(-1)











