一般来讲阻力都是与运动速度或速度平方成正比。一个比较常见的流体阻力公式是
F_D = \frac{1}{2} \rho v^2 C_D A ,
其中 \rho 是流体密度,C_D 是阻力系数, A 是横截面积。
总之 F_D = Cv^2 ,把别的全写成常数就好了。值得注意的是这里我们把物体完全考虑成了横截面相同的,如果飞行中变了,那阻力自然也变了。
至于别的东西就跟平常没啥两样了。这里做个常规的抛物线的例子吧。
u 为起始速度, \theta 为与水平面的起始角度。运行中只受两个力,重力和阻力。用常规方法设定参照系,原点为抛物线起点。
合力: \vec F = \vec F_g + \vec F_D = \begin{pmatrix} -Cv_x^2 \\ -mg - Cv_y^2 \end{pmatrix} = m \vec a = m \frac{d\vec v}{dt} ,
\Rightarrow \frac{d v_x}{dt} = -C'v_x^2 ; \frac{dv_y}{dt} = -g-C'v_y^2 , C' = \frac{C}{m} ,另一个常数。
\Rightarrow \int_{u \cdot cos(\theta)}^{v_x} - \frac{1}{v_x'^2} dv_x' = \int_{0}^{t} C' dt' ; \int_{u \cdot sin(\theta)}^{v_y} \frac{dv_y'}{1 + cv_y'^2} = \int_{0}^{t} -g dt' , c = \frac{C'}{g} ,同样常数而已。
第一个是
[\frac{1}{v_x'}]_{u \cdot cos(\theta)}^{v_x} =\frac{1}{v_x} - \frac{1}{u \cdot cos(\theta)}= C't ,
第二个
\int_{u \cdot sin(\theta)}^{v_y} \frac{dv_y'}{1 + cv_y'^2} = \int_{0}^{t} -g dt' \\ \Rightarrow tan(\vartheta) = \sqrt{c} v_y' \Rightarrow sec^2(\vartheta) d\vartheta = \sqrt{c} d v_y' \\ \Rightarrow\int \frac{1}{\sqrt{c}}\frac{sec^2(\vartheta) d\vartheta}{1 + tan^2(\vartheta)} = \int \frac{1}{\sqrt{c}}\frac{sec^2(\vartheta) d\vartheta}{sec^2(\vartheta)} = \frac{\vartheta}{\sqrt c} ,
因此
[\frac{arctan(\sqrt{c}v_y')}{\sqrt c}]_{u \cdot sin(\theta)}^{v_y} = \frac{arctan(\sqrt{c}v_y) - arctan(\sqrt{c} \cdot u \cdot sin(\theta))}{\sqrt c} = -gt ,
由此我们就有了
\vec v = \begin{pmatrix} \frac{u \cdot cos(\theta)}{1+ u \cdot cos(\theta) C't} \\ \frac{1}{\sqrt c} \cdot tan[\ arctan(\sqrt{c} \cdot u \cdot sin(\theta)) - \sqrt{c} gt\ ] \end{pmatrix} ,稍微整理一下
\vec v = \begin{pmatrix} \frac{1}{1+ u \cdot cos(\theta) C't} u \cdot cos(\theta) \\ \frac{1}{{1 + \sqrt{c} \cdot u \cdot sin(\theta) tan(\sqrt{c}gt)}} (u \cdot sin(\theta)- \frac{1}{\sqrt c}tan(\sqrt{c}gt)) \end{pmatrix} ,
可以看出来随着时间的增加,x方向上的速度逐渐减小,
而y方向的话也是一个递减的关系,大概的走势可以用
\frac{1 - tan(x)}{1 + tan(x)} 来类比,只是系数不一样。可以看出来跟只受重力时的线性降速是有区别的。(值得一提的是计算中物体向上运动,因此我们用的阻力是向下的,但是如果物体开始下落后,阻力应该是向上的,这个变化在这里是表现不出来的)
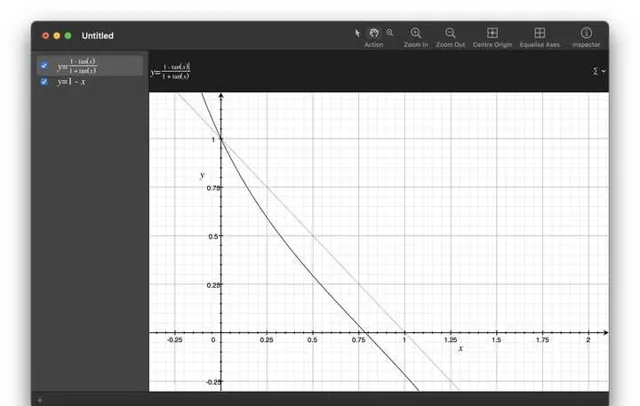
同时,可以看出来当阻力小的时候( C' 和 c 都小的时候), \vec v 会收敛到
\vec v = \begin{pmatrix} u \cdot cos(\theta) \\ u \cdot sin(\theta)- gt \end{pmatrix} ,而这个就是只受重力的时候。
那么运动状态就是 \vec v 再做一次积分,大致明白是个什么情况就好了,这里就暂时不继续往下写了。









