看了一圈答案,有很多遊戲機制、心理學角度解答問題的,不少都回答得很有啟發性,但遺憾的是,唯獨沒有從純數學角度解答這個問題的。
而從純數學角度講,這個問題本質上就是在講「天花板函數的性質」。
在 高票答案 中,作者提到了「最大眾化」的理解:
10% 閃避率 = 受到傷害時有 10% 的概率完全規避這次傷害;10% 減傷 = 受到的所有傷害降低 10%;
—— 事實上,這也是「唯一」準確的理解。
在實際遊戲中,「10% 閃避率」和「10% 減傷」可能會存在一些因為暴露遊戲策劃數學水平不足的歧義理解,比如:
我原本閃避率是 20%,現在又堆了「10% 閃避率」,因此我現在的閃避率是 30%。對嗎?
不對。
正確的說法是:
我原本閃避率是 20%,現在又堆了「10 % 閃避率」,因此我現在的閃避率是 22%;我原本閃避率是 20%,現在又堆了「10 pp 閃避率」,因此我現在的閃避率是 30%;
「百分比」(%)是兩個數「相除」得到的結果;而兩個「百分比」(%)相減,結果應表示為「百分點」(pp)。
因此,在數學表達無誤的情況下, 原問題的理解是唯一的,並不存在歧義。
那麽在這個定義下,理想模型下,相同初始條件時,兩個內容價值相同嗎?
並不相同。
高票答案提出了 EHP(有效生命)的概念,然而這個模型存在一些紕漏,就是它
忽略了邊界條件
。
舉個簡單的例子:你有 100 點血,對手砍你一刀能打 80 滴血,你能抗幾刀?
按照 EHP 的概念,你能抗 1.25 刀;
實際上呢?2 刀。
這個誤差也太大了。
因此,我們需要引入我們熟悉的「天花板函數」:
ceil(x):返回不小於 x 最小整數。假設在正常情況下,對方砍你一刀能砍掉你血量的占比為 k;
那麽:
對於 「10% 減傷」,我們能承受的刀數為:ceil(1/k/0.9);這個值是穩定的。
而對於「10% 閃避」,我們能承受的刀數和運氣相關,似乎涉及到一些風險偏好問題,但學過概率就知道,其總挨刀數的期望是固定的,即 ceil(1/k)/0.9。
那麽, ceil(1/k/0.9) 和 ceil(1/k)/0.9 哪個大?
請看下圖:
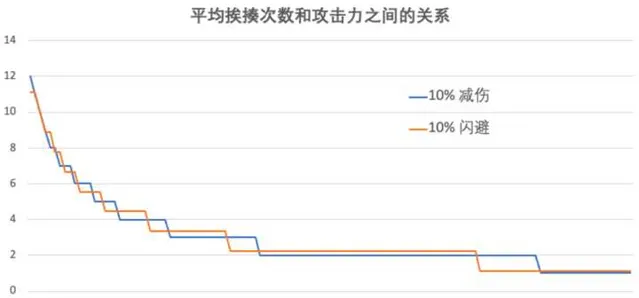
這兩個函數並不是一致的,而是「纏結不清」的。
事實上我們發現,兩個函數孰大孰小,其根本在於 ceil 函數對數值本身的擴大作用;
而從圖中可以明顯看到:
當然,不同的遊戲機制,會導致結果變得完全不同:
—— 如果對手有「連擊加傷」,那麽閃避會提升連擊中斷的可能性,其作用就會明顯變大;
—— 如果對手有「擊中附加負面效果」,比如中毒之類的,顯然閃避的效果更好;
—— 如果自己有「閃避反擊」,顯然閃避更有用;
—— 如果自己有「受傷反擊」,並且反擊強度和受到傷害的程度無關,減傷會讓你的技能依舊發動,那麽減傷的作用就會更好。
由此可見,從遊戲機制講,由於連擊技、附加效果、閃避反擊的廣泛存在, 受傷反擊的技能偏少(有相當一部份還是和受傷血量掛鉤的),在大部份情況下,「閃避率」是更好用的技能——尤其是在考慮人有賭性的情況下。











