作為【訊號與系統】這門課的愛好者。本人也來答一發這個問題好了。
-1.明確【訊號與系統】的學習目標
先要搞清楚為什麽要學這門課,這個非常重要,很多童鞋並沒有搞清楚為什麽要學這門課就已經被裏面的高等數學,復變函數虐的要死要死要死了……之所以要學習訊號與系統這門課,是因為這門課包含了一個非常重要的分析思維:訊號的頻域分析,這是訊號及通訊領域的一個極其偉大的思維。它有兩個特點:
1.簡單清晰:一個訊號的時域波形可能是復雜且難以分析的,但是轉換到頻域後。往往會變得那麽簡單和直白。這種分析訊號頻率成分的思維在通訊和語音領域非常常見。
2.全域性:例如訊號的降噪往往不是針對某一個時間點的而是針對整個訊號時域,這時候就需要頻域分析對訊號進行全域的操作。
舉個例子
例1 .一個加噪的sin訊號我們該如何去除他的雜訊呢?
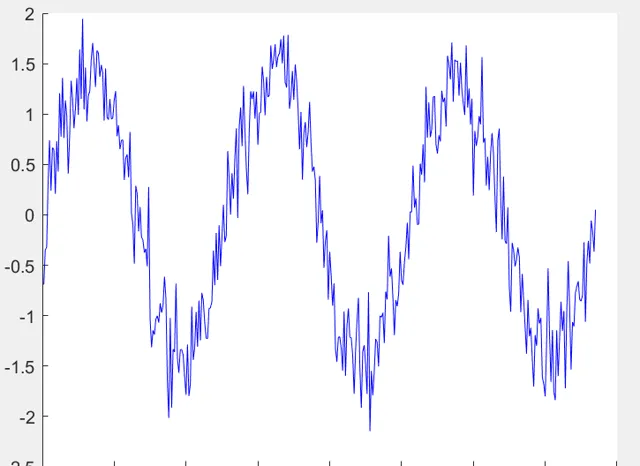
如果現在沒有頻域分析,請問該如何操作呢?那麽這個處理將會變得很難,有的童鞋可能會說,我們平滑(均值濾波)一下這個訊號。那麽請看結果,無疑波形看上去是好了很多,那麽問題來了:為什麽對訊號平滑可以去除雜訊效應呢?
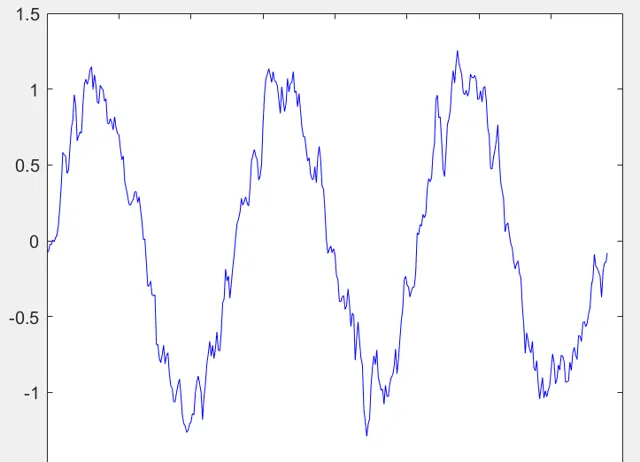
那麽再想下一個問題,有沒有什麽更好的方法可以去除雜訊呢?那麽就涉及頻域分析了,這個時域訊號的波形實在是太亂了,那麽我們不妨將它變道頻域看一下,一變,哎?頻域的形狀是那麽規整
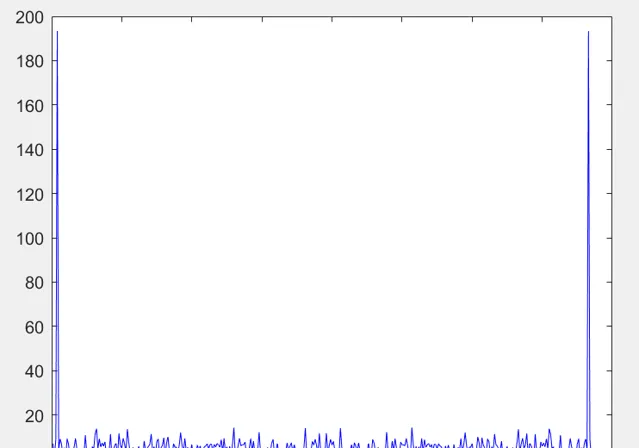
那麽在你學習了訊號與系統理論後你馬上就會知道,這兩個豎條對應著訊號,其他的雜頻對應著雜訊,將訊號透過帶通濾波濾出幹凈的頻譜,那麽再看時域訊號,就變成了標準的sin(其實是包含了微量雜訊的
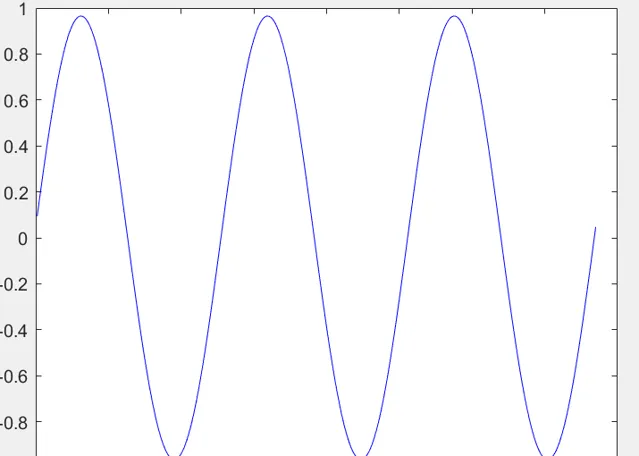
sin訊號,只是雜訊少到人肉眼已經看不出來了),以上就是一個典型的基於頻域的濾波操作,那麽這是訊號與系統所要交給大家的。
例2 .影像銳化及模糊(頻域的方法)
例如很經典的lena圖

經過高頻成分加強(影像透過高通濾波器再與原圖疊加)後(即得到銳化的Lena)

經過低通濾波器後,則得到模糊的Lena

以上並非影像處理領域所采用的演算法,但是以上的演算法很好地展現了訊號與系統的價值,即面向全域的處理以及方便的頻域分析,類似的例子還有很多,其在語音領域的套用更是數不勝數,但是本人並非語音領域,故無法提供相應的例子。
所以單就訊號與系統這門課來說,他是為了交給大家一種時域轉換到頻域的分析思維,所以大家在學習的過程中應該多多關-註訊號與系統的原理,而不要鉆入數學的胡同中,當然數學也是學好此門課的必要條件
0.明確訊號與系統的重要性
透過上面的例子相信大家都已經知道了訊號與系統在通訊及訊號處理中的地位,從學術上看,訊號與系統是很多基礎課的基礎課,諸如通訊原理,數碼訊號處理,語音訊號處理,數碼影像處理,自適應濾波器理論,這些課想學會都必須以訊號與系統學好為前提。二來,訊號與系統更是作為廣大院校IT類專業考研的必考科目,想考研的童鞋們,你說不學好能行嗎?
1.良好的數學功底
想要學好訊號與系統,那必須要有良好的數學功底,訊號與系統將會用到如下的數學
1.【高等數學】:一元微積分,極限,無窮級數,微分方程式,曲線積分
2.【線性代數】:線性空間與線性變換
3.【復變函數與積分變換】:復數的概念,留數的概念,洛朗級數,傅立葉變換,拉普拉斯變換
所以想要吃透訊號與系統,上述數學知識是必不可少的,然而有的同學說這也太多了,都忘了,那麽也無妨,在學習的過程中要經常地回歸數學書本去尋找對應的數學知識,切不可盲目猜測和記憶數學結論。
2.多多關註公式層面的物理意義
如果你把訊號與系統學成了復變函數,那麽我只能說:革命尚未成功,同學仍需努力。訊號與系統這門課具有很強的數學性質,往往使人容易過分關註數學的運算而忽略了物理意義本身,而國內各大教材又總是把重心放在數學上,使得廣大同學很難關註物理意義本身,那麽怎麽辦呢,那麽就需要大家多思考了。比如舉個例子
例3 .傅立葉變換的微分性質在影像處理中的套用
如大家知道的:如果f(t)的傅立葉變換是F(w),那麽f'(t)的傅立葉變換就是jwF(w),那麽這反應了什麽呢?我們看看訊號的幅頻,從|F(w)|變成了w|F(w)|。這說明了比起之前高頻部份被加強了,低頻部份被減弱了。那麽比如我們對Lena圖做差分(離散的微分),會怎麽樣呢?

得到這種圖,可見影像輪廓得以保存(當然各種雜訊也被加強了),這是為什麽呢?因為輪廓其實是影像中灰度變化劇烈的地方,其對應高頻,而非輪廓部份,變化不劇烈,則對應低頻,則濾除,不見了。所以這更加反映了傅立葉變換的微分性質。
這類對於原理的思考,就需要大家平時多多想了,只要樂於思考,肯定學的好訊號與系統的意義
3.應對考試要溫故而知新
如果目標是應對考試,那麽要多做總結多推到以及配合常見結論的記憶。諸如常見訊號的傅立葉變換表、拉普拉斯變換表、Z變換表以及三大變換的性質表,記下來肯定是必須的。這樣考試時才能得心應手,必經訊號與系統數學性質很強,考試出側重數學的題目一來更有區分度二來可以考研一個學生的數學水平(很多高校看中的)
4.有不明白的東西要多參考網上的其他前輩們寫的精華
諸如另一個回答的「卡夫」答主所說的「深入淺出通訊原理」,再比如很出名的如果看了這篇文章你還不懂傅立葉變換,那就過來掐死我吧。此類網上的網誌比比皆是,大家要多多利用
5.選一本適合自己的教材,也可參考公開課影片
首當其沖的教材推薦當然是奧本海姆的兩本名作【訊號與系統】,【離散時間訊號處理】,不適合初學者通覽全書,但是絕對是經典中的經典,適合大家沒事拿出來翻翻,參考。同樣奧本海姆的訊號與系統在網易還有公開課,搭配其原版教材可以事半功倍。
先說這麽多,希望大家學習順利,以上是我個人學習經驗,僅供大家參考











