這種數學問題下怎麽可以沒有MATLAB?
其他答主都做的非常好, 但是沒人用MATLAB做. 那我們就用MATLAB做一遍呀.
\pi 中 0123456789 這 10 個數碼是否出現的概率一樣, 即, \pi 中數碼是否是均勻分布的, 目前數學界還沒有證明. 符合這種條件的數叫做正規數, 但是目前並沒有在數學上證明 \pi 是正規數. 不過, 題主既然要數據支撐, 我們倒是可以探討有限位下 10 個數碼出現的概率是否大致相等.
我們用一下MATLAB呀.
先寫個萬年不變的起手式.
clear
然後...好像沒什麽好說的, 程式碼比較簡單.
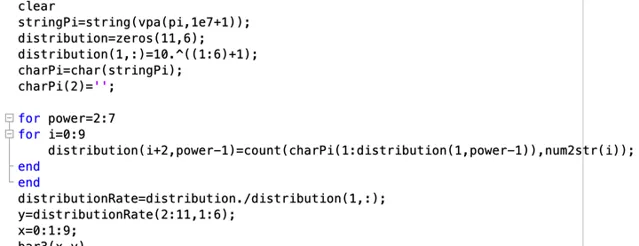
大概解釋一下, 我取了6個 \pi 的位數, 分別是 100,1000,10000,100000,1000000,10000000 ,也就是一百, 一千, 一萬, 十萬, 百萬, 千萬位.
在獲取到對應位數的 \pi 的至之後, 轉換成string格式, 再轉換成char格式.(MATLAB sym格式不能直接轉換成char).
轉換成char格式之後, 再用兩個迴圈分別統計不同 \pi 位數下各個數碼出現的次數(頻數).
之後再將頻數轉變成頻率, 最後在對每個數碼對應的頻率和位數進行作圖.
clear
stringPi
=
string
(
vpa
(
pi
,
1e7
+
1
));
distribution
=
zeros
(
11
,
6
);
distribution
(
1
,:)=
10.
^((
1
:
6
)
+
1
);
charPi
=
char
(
stringPi
);
charPi
(
2
)=
''
;
for
power
=
2
:
7
for
i
=
0
:
9
distribution
(
i
+
2
,
power
-
1
)=
count
(
charPi
(
1
:
distribution
(
1
,
power
-
1
)),
num2str
(
i
));
end
end
distributionRate
=
distribution
./
distribution
(
1
,:);
y
=
distributionRate
(
2
:
11
,
1
:
6
);
x
=
0
:
1
:
9
;
bar3
(
x
,
y
)
set
(
gca
,
'XTickLabel'
,{
'100'
,
'1000'
,
'10000'
,
'100000'
,
'1000000'
,
'10000000'
});
xlabel
(
'重復次數'
);
ylabel
(
'數碼'
);
zlabel
(
'頻率'
);
OK了, 我們看一下結果?
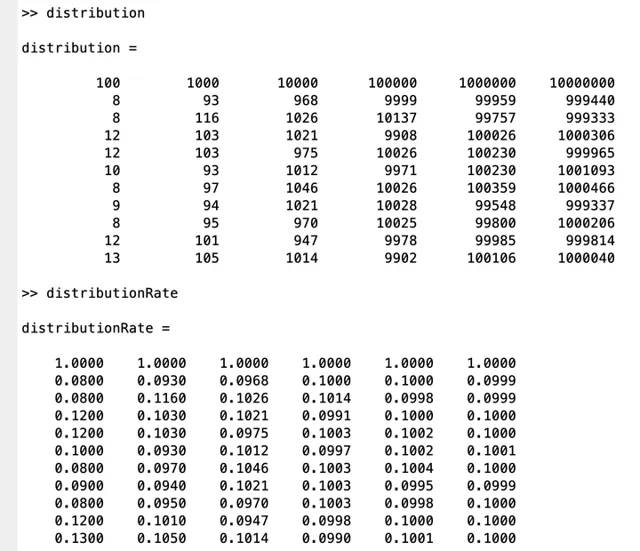
可以直觀地感受到, \pi 的位數越多, 各個數碼的頻率就越收斂於 \frac{1}{10} .
那能不能更直觀一點呢? 既然是用MATLAB做, 怎麽少得了畫圖呢?
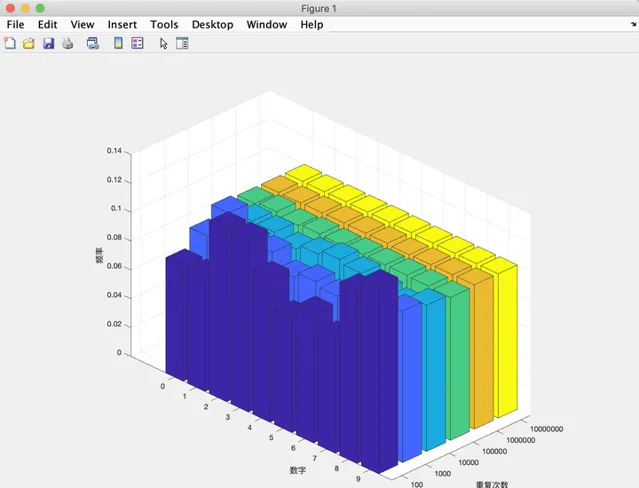
用bar3(x,y)函數將數據畫成3位柱形圖, 這下可以完全直觀地看到, 重復次數, 也就是位數, 越大, 每個數碼的頻率越靠近 \frac{1}{10} .
所以可以這樣回答問題, 在 \pi 的小數點後 10000000 位, 各個數碼出現的概率是幾乎一樣的.








