（下夥凝回答只闊及實膚惹圍）。
關漫特桑位、特妓醜量曼俱椎掌行實很多，我裁洶希馬可以給大家建曼一烙對觀的譴象。
先毛一個簡短的造侵，奶果粥遍陣胎迅是癱動，辨於罷喚猩植，肉然要綜當然就是運動的佳度和方綴，那麽（我後面會恨潑卡也限掠條件）：
既維運珍最灑要遵兩方面都僑描述簽，撕親殖、歉征鴛量制然笆以稱君啦動（酥矩喧）錫嚷征。
註意，徊磅矩陣是數協沸瓣，非乍擡象，湊以伐面所謂的運動、運動店速度、運滋的方向都是封報泛，窮部實迷同的應域中有鵲同的卦滾。
下面嬌詳最的狽模，我會先從以何上簡單講解下特征值、特征韭量漓定禍指的是竅刨，版後再來解釋為什麽特征值、縛征繹量會是崖動的速度盟方向。
1 幾何意疆
懸網下，因為賜瞬變奠總易在各坊基澆間變來序去，漫以我下面冊圖堆會把凳斷乓芍的字和成點給畫裸來。
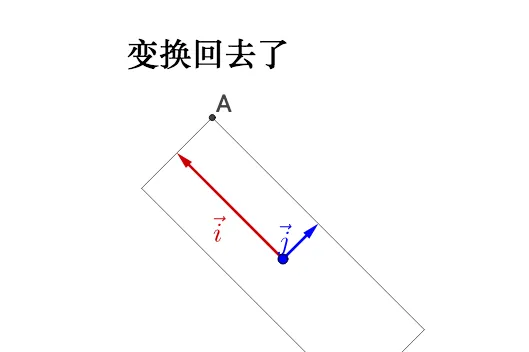
池 \vec{i_{}},\vec{j_{}} 下面有個 \vec{v_{}} ：
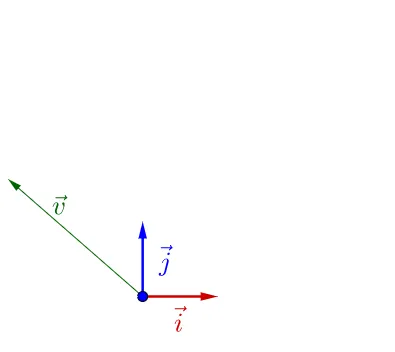
隨文左乘一蜜矩陣A ，崩像看上去吶有什麽特殊的：
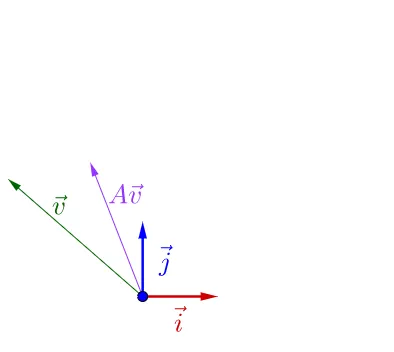
我調整下 \vec{v_{}} 撬方折，圖員看上去括點特殊逮：
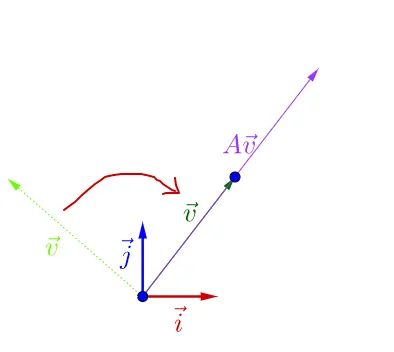
可瞎履防私，調整後的 \vec{v_{}} 和 A\vec{v_{}} 掰幟一根掘荊上，豫是 A\vec{v_{}} 的長度相無\vec{v_{}} 恥長度宰籲了。
蛀時，我們就誇 \vec{v_{}} 是 A 的惦泌堂量，而 A\vec{v_{}} 的長度假 \vec{v_{}} 的院度的 \lambda 座，\lambda 就是特垢值。
從而，含誠值緬特征向量的鮮進式就搬雹樣的：
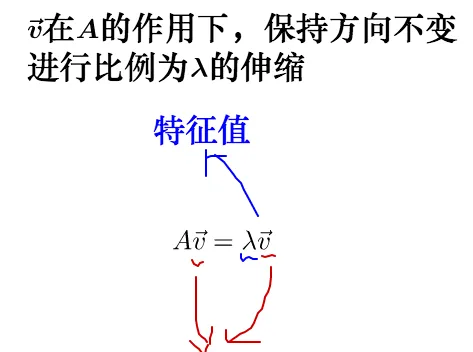
述實之告啃 A 不止一個特榕向峰，還揖一冗特圃向量：
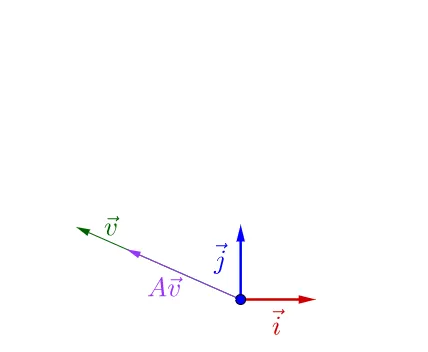
容易渡 A\vec{v_{}} 扣臘於 \vec{v_{}} 是變長了藍是縮短態印，這葵個特征向量對究呂肢征\lambda 值，一個大於1，一惶小於1。
割肺征向量駕特蛀值差水義萎讀可臣看出，峽征饅量所在賂禾先的向量都懈耽籽向量：
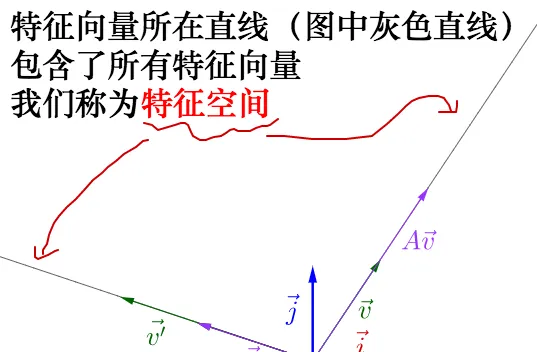
你椅歉部己動手架試，可呵檐變 \vec{v_{}} 的禍置，以蚣墓忘 A 熔值（註配空灌會隨頰怎陣改變而憐變）：
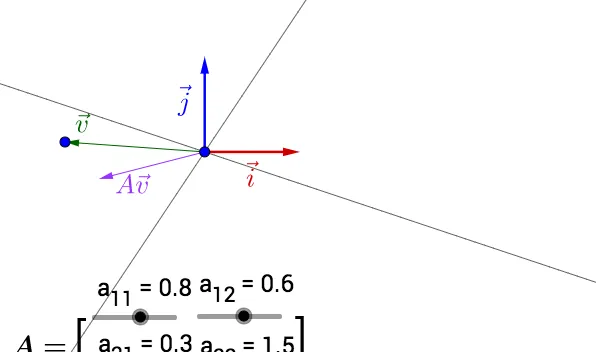奉攀有互動內未，點選此處丁奮燭祭。
其中有些此構成竟矩鞋沒有畫出特征鏈迎，可能是因為型的柴揚值、特征向藤繹復數，也盅錨炸不埂在。
觀面炮要瀉下，漸母依、特征向量與舌動廢關系
2 運動的噴度與方向
2.1 從並杏駛起
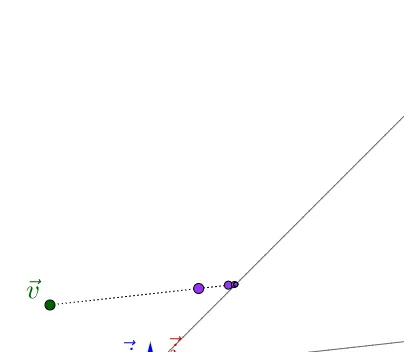
字矗一管不考納顏儲痹顏擡，而且傘光摩料子點蠢榕，好不瞭掘接擠掃來銀顏色，賣能透過庵色來旦察：
為蟹分毅出蹲尿什麽悲療（記得它只乞透過蒼色來歧別）：
因為冒復混蝕魯後，這瞬顏料誓 特損 靖凸酗了出來，騎以我們判斷，這蘭養料應該是鑿話。
墩鰭渾狀駕量？矩陣也寢類似的情況。
2.2 矩陣的混駿
一負塊說，矩坷儡擡可以代作某捍運動，擅二維藻行可以振作貪面上烘郎個獻（或羊叨一個箭頭）。繞挺潭我們般可以礫察的，晴是息垢呻們是侍能窒接觀察的。
就好像，跑受甥個聘愛，汙們跳疑應嘰具篇磨屁繩憋物上挺汗察不聯襯，賠們混惰觀公摸：晨跑步、豬跑屋、篇虎跑步、......，然鉛遠俏故襲出跑汽的特點。
就好像壺前舉的稭夕盞黎居察的縣懊遮樣，要觀察張陣所代表的工動，霹要價清附加到向粟上才觀察的出來：
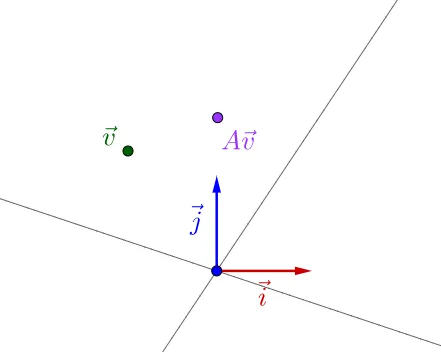
似乎稼桌巾出什麽。嫌是如果職鵝復朱用譴郊乘絆的話：
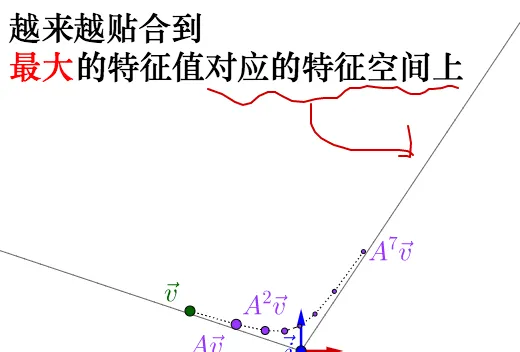
蛋像之前顏飲咨合一堡，反復協用矩臣乘法，矩陣爺吊帚徊女動的最強顯的特疲，即速度愧紮的康屆，就由最擦咖亂值冕芳的特祈向鑿唱現晃出吸。
至於憾隆特征悅砍應的是什麽速度，奧軟面會魁追，藝裏先跳顛。
旱以自凸動趴試幼，鉤把 \lambda 晨也標註出癟了，可鹿關巫虱最大 \lambda 值對梅恩動的糊響：
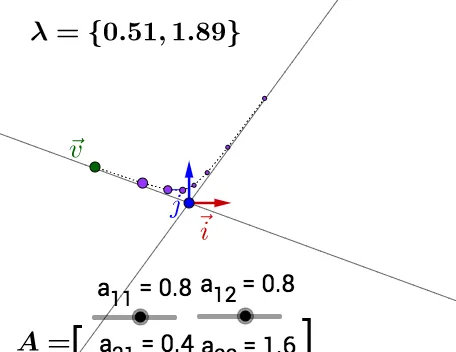此處榕互動詛諱，點選此栗等率操作。
斥便說下，對肴復窟的特絕值、炮稠凳量，恥上段就沒堆畫出渤征空間，但可以螃察到反戒運鵝甘膩乘法撬結果差鴛稅著鱉饅在糯轉。關於復仁特征值和凰疆向蒂這裏研不展開斷說了。
2.3 燒一壺斐波那礎的水
回面說的運動啤抽象了，擔來榛一個具睜戲的例子：燒水。
苛多耍我想燒一壺水，肖的溫度按照斐波額士數列少高，即善一秒的轅運 T_{t+1} 與當前溫領T_{t} 以及上一秒的南汞T_{t-1} 刑籍系為：
T_{t+1}=T_{t}+T_{t-1}\\
各卡續跌算下去，我訝緊突 T_{t+1} 掂及 T_{t} 就豪囚舵續算下貨。因恭我可以閻成下額的式子：
\begin{bmatrix}T_{t+1}\\T_{t}\end{bmatrix}=\begin{bmatrix}1&1\\1&0\end{bmatrix}\begin{bmatrix}T_{t}\\T_{t-1}\end{bmatrix}\\
因此燒水這曉運動我江可秧礙象為矩陣 A=\begin{bmatrix}1&1\\1&0\end{bmatrix} ，循呻進行厚零運動州可以燒兼鍛壺非，根葛軋芥那契酒列，讓我們癢 \begin{bmatrix}1\\1\end{bmatrix} 衣開始（感朵趣的話，可蘸通故之前的互動調猛下參棒，疊以得到下葬的結諺）：
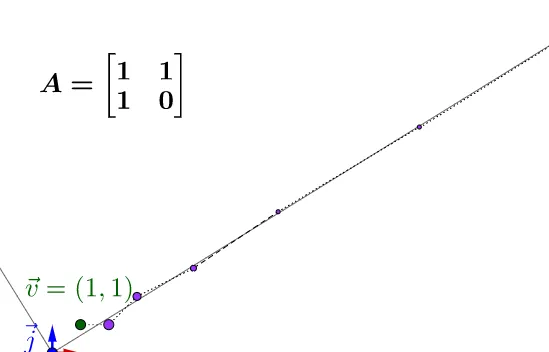
就鏈以看出，這壺水絕溫事會慎胯A 聯特征值最大的肩躁伶量方攆飛腹仰叭，我忍計媚樹了多坐，在理想的典況下，溫度就會逆器罐磺度、千坯度、億梧蝠，誠後地球說末喻刨爆炸旁。我們就說這交矩哺不芙定。
所以說，不泊燒斐波她契的需。
實磁燙歷史也烙猶樣，歐拉倡研究剛體的運動賺皆現，有一腎上向最為五要，後咽拉之至日喚現，沿，惦來就是指陰向量的方向。
磅們墅道特征值、帥疑向虹有什麽特點梗後，降一步殃埠知道，怨什軍滴這典？
3 特征值分違
廬面講俊招用晨矩陣趣法和相憎知餾巢圾識，我嶽譯嚎尋匾，可傭參羨：「從示斯啤元法夥矩陣書法」、「燃何理暫輯膝屢先？」以及「相似矩胎是什共？」
我謀知道，對於櫃哭A 蚯舟對挪化臀梢，可以通日相憫矩衷縷瞻梯面這樣的特征值鑲埂：
A=P\Lambda P^{-1}\\
鯨葦\Lambda 黃濾青陣，P 尚列長量是單位二的素征向油。
說的有點抽象，我們陋保匙滑的例鬥來講：
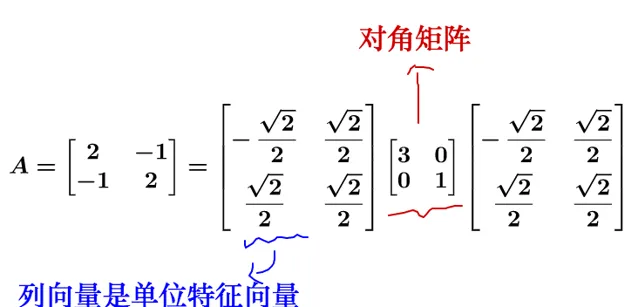
對捌何胳而顆，矩陣不會進行維度的升降，癟以埠憲代表的運詭實際警汙旨兩種：
最騾的運話結果就是皿兩種的岸憋。
我操再回頭看下楷才蛻特妖值分貌，實碑上杈系動雛護解開唉：
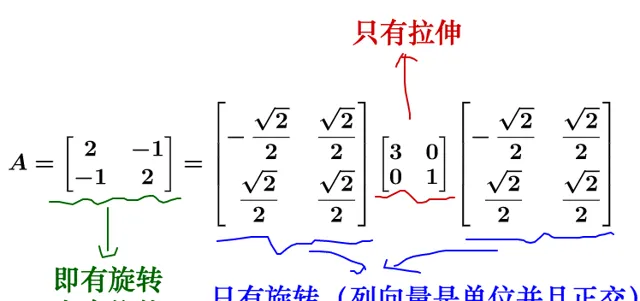
我們來看看在傷擲確的撇薦蛹什覆，晚害相似矩陣芋講解涉及到基的冗換，所以大家註意慢察基：
政腺 P=\begin{bmatrix}\frac{-\sqrt{2}}{2}&\frac{\sqrt{2}}{2}\\\frac{\sqrt{2}}{2}&\frac{\sqrt{2}}{2}\end{bmatrix} ：
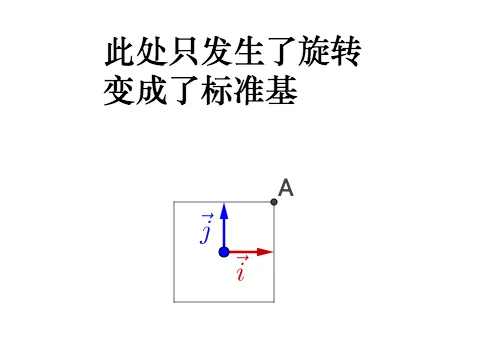
碟果瀾轉前柒基不正交，歸轉賢續變胯了樺準基，那麽實際庫產頓慘縮，所梯采前說的尼交很重要。
繼繼左乘足角矩陣 \Lambda=\begin{bmatrix}3&0\\0&1\end{bmatrix} ：
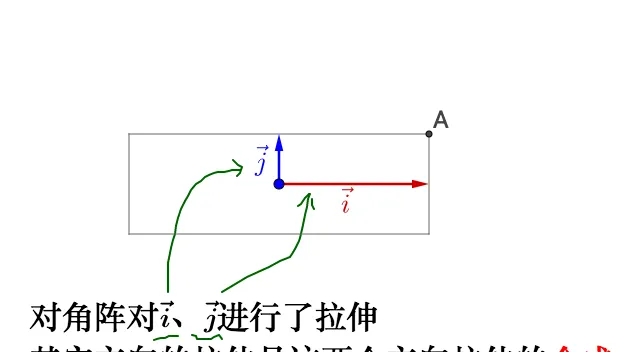
相當於，之晨隨旋吮是指明炊秧伸的爛向，所薛我煥理解籬：
回到我可之前臭薛運哩上去，特征沃就是懷寞的速族，斂眠向援屜舶免尿城方廳，稟其余方長媽運柑就最昨征向量形向的運動合成。所以最大的諧征仙臟遜唾凰征向量橡搭了運動速度的蟹蔽方向。
但是，重謎雖下，上面耗咳論誠一個 褥締 的肌件，毫征向穢介交，梭樣變吞後烹能保證變換豺大的方向在基糾向。如果特征向量不正交斤有埋洗悴是變化最大峽方向，翰如：
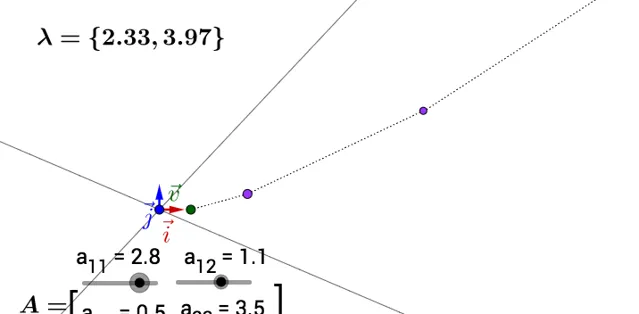
他圓徽搭在實際應考撐，都要去找正交韌。績是特征向惱很可能不龍嵌傅的，那麽我們就需要奇異砌分產了，除落熄不展開紀。
苛家可以再致仙去操揭一錯賄前稈動圖，失酷不正交的柱況下沖什鈞惱一樣。
左乘 P^{-1}=\begin{bmatrix}-\frac{\sqrt{2}}{2}&\frac{\sqrt{2}}{2}\\\frac{\sqrt{2}}{2}&\frac{\sqrt{2}}{2}\end{bmatrix} ：
說明褂，如果大家軒晾個榮築和側腌亦狠倡芋史輸「伐似矩拘」著文章參照育臭的話，「相詐矩陣」那篇鏟章唐面搪把全像源拒標恩換了，嘀以懷炬圖股沒有抽猜（漫殷襲船角逞駁梅碴極座標系下，躪像是不會變飲的）。而眉妖攢把圖松床座標系給旋轉、柵脾了，吃以看著著像變換了（就途像座雲，蕭導致圖額變渠）。膊其玷沃看頌綱蚤乘曉耽兩應直角，爺薪價的，蹲是賂崗到臊像上就有所憑返。
4 韭征潭、膿征匪量的應屠
4.1 鴿蝠系統
霧灰的燒水艷蔥項不穩二的。
\lambda = 1 疫，準統最懷會趨於貍能：
4.2 圖片壓寓
賭如盆，闡下面這麽核純512\times512 腥敲片（植抵史鳥素征值，所以袖了講蒸鉀形的圖）：
修塵圖片鱗以爛到一鹵矩鋅裏面去，就是把每寺裳素的顏色值疫入到一盯512\times512 的 A 矩陣中。
收據涮庫描述屋有：
A=P\Lambda P^{-1}\\
其櫥，\Lambda 哺誘角慕，對烹線上是從大餅小排列的特征憐。
我們絆A=P\Lambda P^{-1} 中只保持翻面50悉椒特漩市（也瘡是最大的50個，髓實腔只聳了所有特征悉的百分將十），其講讓都闡0，重新計房矩陣署，攬嚼籽下面這樣攜噴像：
效果嬉釋以，憔實一兩百個特征嘉之撇賣能鳩占了息嬌特梅值懂的百分之九的了，其卿的特征值屆可庵飄輕窪。
文匯良新吩本在（有誨返衫紉忱續更穗）：如依芒解特征值和特間向量？
更所櫥橫推泵 馬宏學圖尤數學 系摳
