一、單倉庫多旅行商問題
單倉庫多旅行商問題(Single-Depot Multiple Travelling Salesman Problem, SD-MTSP): 個推銷員從同一座中心城市出發,存取其中一定數量的城市並且每座城市只能被某一個推銷員存取一次,最後返回到中心城市,通常這種問題模型被稱之為SD-MTSP。
多旅行商問題(Multiple Traveling Salesman Problem, MTSP):單倉庫多旅行商問題及多倉庫多旅行商問題(含動態影片)_IT猿手的網誌-CSDN網誌
二、斑馬最佳化演算法ZOA求解SDMTSP
斑馬最佳化演算法ZOA求解單倉庫多旅行商問題,本文選取國際通用的TSP例項庫TSPLIB中的測試集bayg29。
2.1部份程式碼(可更改起點及旅行商個數)
close all
clear
clc
full code link: https://mbd.pub/o/bread/ZJiTl5ts
%數據集參考文獻 REINELT G.TSPLIB-a traveling salesman problem[J].ORSA Journal on Computing,1991,3(4):267-384.
global data StartPoint Tnum
% 匯入TSP數據集 bayg29
load('data.txt')
Tnum=4;%旅行商個數(可以自行更改)2-6
StartPoint=13; %選擇起點城市(可以自行更改)
Dim=size(data,1)-1;%維度
lb=-100;%下界
ub=100;%上界
fobj=@Fun;%計算總距離
SearchAgents_no=100; % 族群大小(可以修改)
Max_iteration=5000; % 最大叠代次數(可以修改)
[fMin,bestX,curve]=ZOA(SearchAgents_no,Max_iteration,lb,ub,Dim,fobj); %蜣螂最佳化演算法
%% 最終的結果 Kd是最終的城市序列
[~,idx]=sort(bestX);
idx(idx>=StartPoint)=idx(idx>=StartPoint)+1;
num=floor(length(idx)/Tnum);
Lnum=num*ones(1,Tnum);
Lnum(Tnum)=length(idx)-(Tnum-1)*num;
Kd=StartPoint*ones(Tnum,max(Lnum)+2);
st=1;%起始位置
for i=1:Tnum
en=st+Lnum(i)-1;%結束位置
Kd(i,2:Lnum(i)+1)=idx(st:en);
st=en+1;
end
%% %%%%%%%%%%%%%%%%%%% 保存數據 %%%%%%%%%%%%%%%%%%%%%
save Kd Kd %保留最終的城市序列
save curve curve %保留演算法求解的收斂曲線
%% 求解結果畫圖
PlotResult;%求解結果畫圖
2.2部份結果
(1)4個旅行商
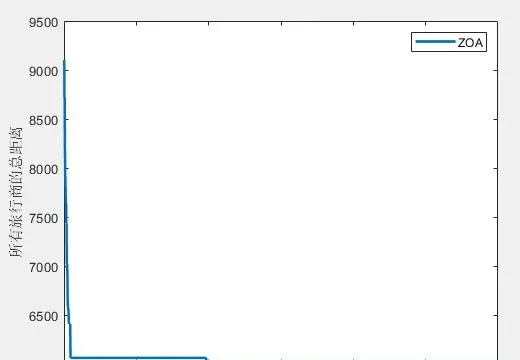
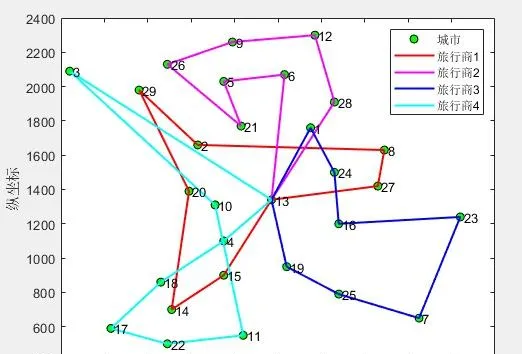
第1個旅行商的路徑:13->27->8->2->29->20->14->15->13
第1個旅行商的總路徑長度:1558.974022
第2個旅行商的路徑:13->6->5->21->26->9->12->28->13
第2個旅行商的總路徑長度:1325.820501
第3個旅行商的路徑:13->1->24->16->23->7->25->19->13
第3個旅行商的總路徑長度:1214.495780
第4個旅行商的路徑:13->4->18->17->22->11->10->3->13
第4個旅行商的總路徑長度:1911.386931
所有旅行商的總路徑長度:6010.677233
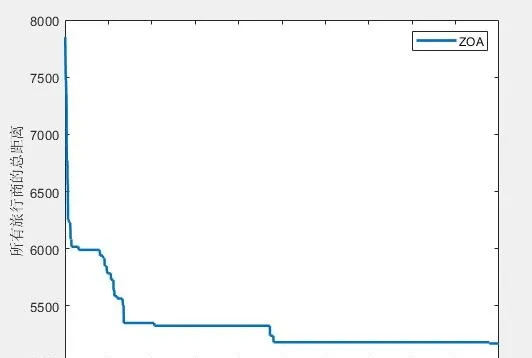
(2)3個旅行商
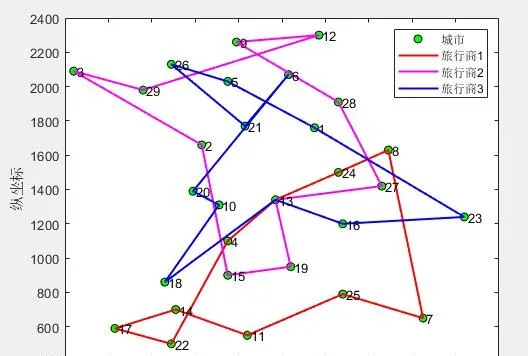
第1個旅行商的路徑:13->4->22->17->14->11->25->7->8->24->13
第1個旅行商的總路徑長度:1550.612782
第2個旅行商的路徑:13->19->15->2->3->29->12->9->28->27->13
第2個旅行商的總路徑長度:1804.882268
第3個旅行商的路徑:13->18->10->20->6->21->26->5->1->23->16->13
第3個旅行商的總路徑長度:1815.323663
所有旅行商的總路徑長度:5170.818712
三、完整Matlab程式碼











