关于超光速旅行的疑问层出不穷,不断有人试图突破爱因斯坦的限制,比如通过叠加速度来达到超光速。然而,我们心知肚明,若真能如此,那相对论怕是早已成为历史。就拿小学生都懂的速度叠加公式来说,连他们都明白,像爱因斯坦那样的天才自然也了然于胸。

因此,关于借由速度叠加突破光速的假设,显然站不住脚。可为什么总有人沉溺于这种设想呢?尽管明知其不可为,为何还是如此纠结?
实际上,这种纠结在一定程度上是合情合理的。在我们学生时代,至少在高中以前,伽利略变换是我们计算相对速度的唯一工具,它的数学表示为V=V1+V2。
然而,伽利略变换仅仅适用于我们日常所处的低速环境,它背后蕴含的是绝对时空观——即我们所生活的时空是绝对不变的。例如,我们眼中的一段距离和别人眼中的同一段距离是相同的,无论我们处于何种运动状态。同样,我们所感知的时间也是如此,每个人的一秒都是一样的。

绝对时空观与我们的日常生活经验完美契合,因此,我们总是不自觉地陷入这种观念的框架中,哪怕是在思考亚光速运动时也一样。但实际上,如果我们真的进入亚光速世界,时间和空间的性质将变得模糊和不确定,每个人对它们的感知也将大相径庭。
这背后的原因在于,我们生活的世界并非绝对时空,而是相对时空。只不过在我们的低速世界里,时间和空间的相对性并不显著。但如果速度足够快,比如卫星导航系统,即使时间的相对性微乎其微,我们也必须将其考虑在内。

在亚光速领域,我们更需考量时间膨胀和尺缩效应,此时要用洛伦兹变换来计算相对速度。简单来说,伽利略变换只是洛伦兹变换的一个特例,一种近似值。在速度极小时,洛伦兹变换的结果与伽利略变换相近。但当速度为光速时,洛伦兹变换得出的相对速度仍为光速,而非两倍光速。
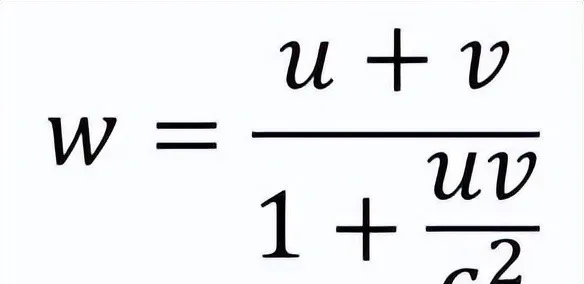
有些人不理解这一概念,主要是因为他们在思考时依旧默认使用牛顿的绝对时空观,甚至可能未曾意识到这一点。还有一个常见错误是混淆参照系,导致逻辑混乱。
回到问题本身,有人可能会质疑:假设不考虑两个以光速反向飞行物体间的相对速度,如果它们各自飞行一年,那它们相隔多远呢?这里的「一年」涉及到参照系的选择。以人类的视角来看,答案是两光年。但对于两个物体来说,它们之间的距离并非两光年,而是一光年。

当然,所有这些都建立在理论假设之上,因为现实中物体无法达到光速,我们只能模拟接近光速的情况。但重要的是,我们要理解绝对时空观与相对时空观的区别,以及参照系选择对结果的影响。
简言之,低速领域适用伽利略变换,高速领域则用洛伦兹变换。从牛顿到爱因斯坦,对时空观的认知经历了漫长转变,涉及到麦克斯韦方程组、洛伦兹变换、以太的概念等诸多内容。若要探讨为何速度会影响时间和空间,则需更多篇幅来解释,此处不再赘述。











