授人以鱼不如授人以渔,这篇文章会介绍 如何通过「统计学检验」来对比机器学习算法性能 。掌握了这个方法后,我们就不需要再人云亦云,而可以自己分析算法性能。
首先结论如下,在对比 两个算法 在 多个数据集 上的表现时:
在对比 多个算法 在 多个数据集 上的表现时:
文章结构如下:(1-2) 算法对比的原因及陷阱 (3-4) 如何对比两个算法 (5-6)如何对比多个算法 (7)如何根据数据特性选择对比方法 (8)工具库介绍。
1. 为什么需要对比算法性能?
统计学家George Box说过:「All models are wrong, but some are useful」(所有模型都是错误,只不过其中一部分是有价值的)。通俗来说, 任何算法都有局限性,所以不存在「通用最优算法」,只有在特定情境下某种算法可能是渐进最优的 。
因此,评估算法性能并选择最优算法是非常重要的。不幸的是,统计学评估还没有在机器学习领域普及,很多评估往往是在一个数据上的简单分析,因此证明效果有限。
2. 评估算法中的陷阱
首先我们常说的是要选择一个 正确的评估标准 ,常见的有:准确率(accuracy)、召回率(recall)、精准率(precision)、ROC、Precision-Recall Curve、F1等。
选择评估标准取决于目的和数据集特性。在较为平衡的数据集上(各类数据近似相等的情况下),这些评估标准性能差别不大。而在数据严重倾斜的情况下,选择不适合的评估标准,如准确率,就会导致看起来很好,但实际无意义的结果。举个例子,假设某稀有血型的比例(2%),模型只需要预测全部样本为「非稀有血型」,那么准确率就高达98%,但毫无意义。在这种情况下,选择ROC或者精准率可能就更加适当。这方面的知识比较容易理解,很多科普书都有介绍,我们就不赘述了。
其次我们要正确理解 测量方法 ,常见的有
举个例子,我们想要分析刷知乎时间(每天3小时 vs. 每天10小时)对于大学生成绩的影响。如果我们使用相同的20个学生,观察他们每天3小时和10小时的区别,那就是重复测量。如果我们选择40个学生,分成两组每组20人,再分别观察那就是独立测量。如果我们先找20个学生,再找20个和他们非常相似的大学生,并配对观察,就是成对相似。
我们发现,当错误的理解测量方式时,就无法使用正确的统计学手段进行分析 。
在这篇文章中我们默认:评估不同算法在多个 相同数据集 上的表现属于 重复测量 ,而特例将会在第七部分讨论。同时,本文介绍的方法 可以用于对比任何评估标准 ,如准确度、精准度等,本文中默认讨论准确度。
3. 两种算法间的比较:不恰当方法

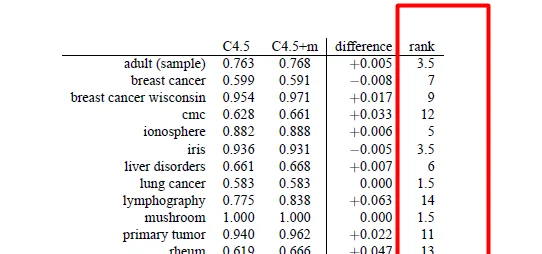
图1展示了两种决策树方法(C4.5,C4.5+m)在14个数据集上的准确率。那么该如何对比两种算法呢?先说几种错误(不恰当)的方法:
不恰当方法1:求每个算法在所有数据集上的均值,并比较大小 。错误原因:我们对于算法在不同数据集上错误的期望不是相同的,因此求平均没有意义。换句话说,数据不符合相称性(commensurate)。
不恰当方法2 : 进行配对样本t检测(Paired t test) 。显然,t test是统计学方法,可以用来查看两种方法在每个数据上的平均差值是否不等于0。但这个方法不合适原因有几点:
不恰当方法3:符号检验(sign test) 是一种无参数(non-parametric)的检验,优点是对于样本分布没有要求,不要求正态性。比较方法很简单,就是在每个数据集上看哪个算法更好,之后统计每个算法占优的数据集总数。以这个例子为例,C4.5在2个数据集上最优,2个平手,10个最差。如果我们对这个结果计算置信区间,发现p<0.05需要至少在11个数据集上表现最优。因此这个方法的缺点有:

4. 两种算法间的比较:推荐方法
考虑到通用性,我们需要使用非参数检验。换句话说,我们需要保证对样本的分布不做任何假设,这样更加通用。
方法1:Wilcoxon Signed Ranks Test(WS ) 是 配对t检验的无参数版本 ,同样是分析成对数据的差值是否等于0,只不过是通过排名(rank)而已。换个角度看,我们也可以理解为 符号检验的定量版本 。优点如下:
方法2(详见第七部分):Mann Whitney U test (MW)和WS一样,都是无参数的且研究排名的检验方法。MW有以下特性:
换句话说,MW是当样本量不同时才建议勉强一试,因为不符合独立测量的假设。不同数据集的错误(准确率)不一定符合特定分布,很可能不符合相称性,但在特定情况下有用,详见第七部分。
总结:如果样本配对且符合正态分布,优先使用配对t检测。如果样本不符合正态分布,但符合配对,使用WS。如果样本既不符合正态分布,也不符合配对,可以尝试MW。
5. 多种算法间的比较:不恰当的方法
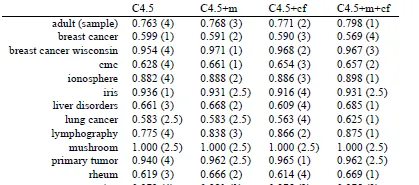
图4提供了四种算法(C4.5,C4.5+m,C4.5+cf,C4.5+m+cf)在14个数据集上的准确率。
不恰当方法1 :一种看法是,我们是否可以把两个算法的对比推广到多个算法上。假设有k个算法,我们是否可以对它们进行两两比较,经过 \frac{(1+(k-1))\times (k-1)}{2}=\frac{k^2-k}{2} 次计算得到一个矩阵。这个是经典的多元假设检验问题,这种穷举法一般都假设了不同对比之间的独立性,一般都不符合现实,需要进行校正,因此就不赘述了。
不恰当方法2 : Repeated measures ANOVA 是经典的统计学方法,用来进行多样本间的比较是,可以看做是t检验的多元推广。ANOVA不适合对比算法表现的原因如下:
不幸的是,我们想要对比的算法表现不符合这个情况,因此ANOVA不适合。
6. 多种算法间的比较:推荐的方法
我们需要找到一种方法同时解决第5部分中提到的问题,这个方法需要:
Demšar [1]推荐了非参数的多元假设检验 Friedman test 。Friedman也是一种建立在排名(rank)上的检验,它假设所有样本的排序均值相等。具体来讲,我们首先给不同算法在每个数据集上排序,并最终计算算法A在所有数据集上排名的均值。如果所有算法都没有性能差别,那么它们的性能的平均排名应该是相等的,这样我们就可以选择特定的置信区间来判断差异是否显著了。
假设我们通过Friedman test发现有统计学显著( p <0.05),那么我们还需要继续做事后分析(post-hoc)。 换句话说,Friedman test只能告诉我们算法间是否有显著差异,而不能告诉我们到底是哪些算法间有性能差异。想要定位具体的差异算法,还需要进行post-hoc分析。
Friedman test一般配套的post-hoc是Nemenyi test,Nemenyi test可以指出两两之间是否存在显著差异。我们一般还会对Nemenyi的结果可视化,比如下图。

另一个值得提的是,即使Friedman证明算法性能有显著不同,Nemenyi不一定会说明到底是哪些算法间不同,原因是Nemenyi比Friedman要弱(weak),实在不行可以对必须分析的算法成对分析。
方法2(详见第七部分):和两两对比一样,在多个样本对比时也有一些特定情况导致我们不能使用Friedman-Nemenyi。另一个或许可以值得一试的无参数方法是Kruskal Wallis test搭配Dunn's test(作为post-hoc)。 这种方法的特点是:
7. 再看重复测量和独立测量
我们在第二部分分析了重复测量与独立测量,而且假设机器学习性能的对比 应该是建立在「重复测量」上的,也就是说所有的算法都在相同的数据集上进行评估 。
在这种假设下,我们推荐了无参数的:Wilcoxon对两个算法进行比较, Friedman-Nemenyi对多个算法进行对比。
然而,「 重复测量」的假设不一定为真 。举个例子,如果我们只有一个数据,并从数据中采样(sample)得到了很多相关的测试集1, 2,3...n,并用于测试不同的算法。
在这种情况下,我们就可以用Mann Whitney U test对比两种算法,Kruskal-Dunn对比多种算法。 而且值得注意的是,这种情况常见于人工合成的数据,比如从高斯分布中采样得到数据 。因此,要特别分析数据的测量方式,再决定如何评估。
8. 工具库与实现
我们知道R上面有所有这些检验,着重谈谈Python上的工具库。幸运的是,上文提到所有检验方法在Python上都有工具库
Scipy Statistical functions :Wilcoxon,Friedman,Mann Whitney
scikit-posthocs:Nemenyi,Dunn's test
文章的配图来自于[1] 以及我的一篇paper [2],接收后会补上reference。 文章的思路和脉络基于[1], 建议阅读。[2]主要着力于特定情况,当重复测量失效时的检验。
[1] Demšar, J., 2006. Statistical comparisons of classifiers over multiple data sets. Journal of Machine learning research , 7 (Jan), pp.1-30.
[2] To complete.











