「怎樣用數學找到一顆遺失的氫彈?」——貝葉斯定理在搜尋失蹤物品方面的幾個小故事
冷戰期間,在西班牙上空曾發生過一次令人難以置信的事故:一場原本是例行公事的飛行活動,最終卻造成兩架飛機墜毀,七名機組人員死亡,整整一個村莊受到汙染,更糟糕的是,一顆氫彈掉到海裏,丟了。一千多名美國和西班牙人員展開了搜尋和清理工作,還出動了十幾架飛機、近三十艘美國海軍的艦艇和五艘潛艇。整個行動花費超過1.2億美元,造成的外交影響更是難以估量。而且頗具黑色幽默意味的是,18世紀曾有人提出過一個不起眼的數學定理,是關於如何在幹草堆中尋找一根真正的針,當時沒人認為這個定理有什麽實用性,可在這次丟氫彈的事件中,這個定理卻提供了無比實用的解決方案。讓我們來看看整個事件的始末:1966年1月17日上午10點左右,駐紮在美國北卡羅來納州的第31轟炸中隊麾下的兩架B-52G轟炸機正在西班牙卡塔赫納西南方的海面上接近兩架KC-135空中加油機,準備接受空中加油。這兩架轟炸機每架都攜帶有四顆爆炸當量為150萬噸梯恩梯的B-28型氫彈。此次帶彈飛行代號「鉻圓頂行動」,是美國核威懾任務的一部份,旨在讓核武裝轟炸機飛到蘇聯的家門口展示力量。

正在接受KC-135空中加油機加油的B-52轟炸機。意外就在這個時候發生了:有一架B-52轟炸機在接近加油機時飛得太快了,以至於後者沒有收到告警訊號,結果這兩架飛機在九千多米高的天上相撞。空中加油機的加油桿撕裂了這架B-52轟炸機的左翼,機上的七名機組人員中,有三人在事故中喪生。機翼斷裂產生的火星引燃了機上的燃油,把整架加油機炸成了一團耀眼的火球。加油機上所有的四名機組人員當場死亡,一百多噸燃燒的飛機殘骸落在了地中海附近一個名叫帕洛馬雷斯的西班牙小村莊裏。與飛機殘骸一同落在地上的,還有那四顆氫彈中的三顆。不到24小時,美國空軍的一支事故處理小組便從馬德裏附近的托雷洪空軍基地趕到了現場。來自洛斯阿拉莫斯國家實驗室和珊迪亞武器實驗室以及空軍後勤部隊的專家們紛紛趕往這個不起眼的西班牙小鄉村。搜尋小組在一天之內就發現了三顆落在地上的氫彈:一顆落在了較軟的土坡上,其外殼相對完整;其余兩顆氫彈內的高爆炸藥(用於產生爆轟波壓縮核物質)在撞擊時被引爆,在幹燥的土壤中炸出了一個直徑30多米的大坑,並把裏面的放射性元素鈈、鈾和氚等灑落得到處都是。

回收的一枚B-28型氫彈。按照慣例,必須找到下落不明的第四顆氫彈,然而,帕洛馬雷斯村所在的艾爾梅裏亞省擁有上千年的采礦業,頻繁的人類活動打出了無數的礦井,原本幹燥平坦的土壤被無數大坑和窪地弄得支離破碎——這些景觀甚至因在那裏拍攝過美國西部牛仔片而聞名。這使得對第四顆氫彈的搜尋變得困難無比。幾個星期內,美軍和西班牙警察用放射線探測器對該地區進行了仔細的搜查,但未能找到第四顆氫彈。這時有目擊者報告說,他看見有物體掛在降落傘下落入了大海。早在事故發生8小時後,美國海軍便下令讓一支艦隊駛往西班牙海岸。事故發生5天後,美國空軍正式請求海軍幫助尋找失蹤的氫彈。為了完成這次任務,美國海軍甚至在其駐地聘請了一名「神童」。
管用的「神童」
這位「神童」名叫約翰·皮納·克雷文,第二次世界大戰期間,他曾在加州理工學院和衣阿華大學學習工程和水利學。當他作為一名文職科學家回到海軍服役後,他解決了美國海軍「如麗螺」號核潛艇的一大結構性問題,還審查了「北極星」潛射彈道飛彈計畫。1963年,美國海軍遇上了一件大事——「長尾鯊」號核潛艇在潛航期間失蹤。海軍方面派克雷文去負責深海救援和打撈研究工作。克雷文當時是海軍特別計畫辦公室的負責人,他出色地完成了工作。三年後,他不得不再次上陣,以找到這顆失蹤的氫彈,而且要快。蘇聯人肯定會竭盡全力地找到這顆氫彈,白宮方面也在施加壓力。林登·詹森總統不相信某些政客做出的保證,即這顆氫彈永遠消失在了大洋裏,任何人也找不到。但是,在數百平方千米的海底影像中找到一艘輕艇大小的物體看上去幾乎是不可能完成的任務。

一名美國海軍的潛水員正在地中海海底回收飛機殘骸,照片來自美聯社。當時,帕洛馬雷斯村有位名叫法蘭西斯科·西莫·奧特斯的漁夫,他曾看到有個帶著降落傘的物體從天而降,還指出了墜落的地方。不過,美國海軍的專家基於他們自己對氫彈下降過程的計算,駁回了這位漁夫的說法。經過潛水員和聲吶為期數周卻無果的海底搜尋之後,克雷文轉向神聖的數學領域尋求幫助。令很多人沒有想到的是,一個不起眼的、誕生於250多年前的機率理論居然讓人們看到了找到氫彈的希望。在一本可追溯到18世紀60年代的未發表手稿中,一位英國皇家學會會員兼統計學家湯瑪斯·貝葉斯首先提出了一種理論,這種理論後來還以貝葉斯的名字被命名為「貝葉斯定理」。簡單來說,貝葉斯定理在數學上描述了如何「根據不確定性資訊做出推理和決策」,即解決條件機率推理問題。
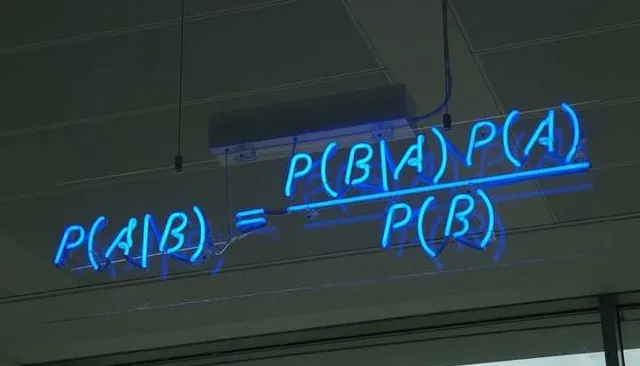
劍橋大學用霓虹燈呈現出的貝葉斯定理公式。克雷文意識到,貝葉斯定理可以幫助改善搜尋團隊關於失蹤氫彈所在位置的觀念。他首先調來了帕洛馬雷斯附近海底的詳細地圖,然後要求他手下的打撈和搜尋專家對氫彈墜落期間可能發生的每一件事都計算機率。例如,氫彈有兩個降落傘,在墜落過程中,一個傘開啟的機率是多少?兩個都開啟的機率是多少?兩個都未開啟的機率是多少?氫彈直接落入水中的機率是多少?如果它以某個特定的角度下落會如何?克雷文的團隊探索了數百種可能,並計算了每種可能發生的機率。
量化的觀念
根據克雷文團隊計算出的機率,這顆氫彈有可能會落在遠離海岸的許多不同地方。然後,克雷文手下的數學家們根據最初的一輪「猜測」和每個指定位置的機率,計算出了每個指定位置有落彈的可能性。
從本質上講,數學家根據他們算出的情況,量化了他們對氫彈落點的猜測。最終,他們將對氫彈落點的猜測反映在了一張海底影像上——這張「機率圖」顯示了最有希望搜尋到氫彈遺失的位置,但這些位置與傳統搜尋技術所認定的位置有極大的差別。數學家們的這張圖表明,這顆氫彈的落點遠不是在飛機殘骸附近。美國海軍派遣科研潛艇「艾爾文」號和「阿魯米納特」號檢查了相關地點,但它們在搜尋一番後無功而返。克雷文團隊根據新的搜尋資訊重新計算了他們的機率。此時,距離氫彈墜落已經過去相當長一段時間了。白宮方面在收到克雷文的最新報告後,強森要求派一群「真正的專家」解決這個問題。但是,在仔細審查了克雷文的報告之後,麻省理工學院和康奈爾大學的一個專家小組一致認為,克雷文所用的這種「奇怪的方法」是最好的方法。與此同時,有人開始重新審視漁夫奧特斯的說法。這位漁夫被邀請到了美國海軍的「品尼高」號踩地雷艦上,並指引著這艘船駛向一片聲吶曾收到過可能是氫彈訊號的海域。這片海域位於克雷文重新計算的最新海圖上的一處高機率地點中。「艾爾文」號潛艇下潛到了2550英尺(約686公尺)深的海底,發現了一個覆蓋在圓柱形金屬物體上的降落傘。這艘潛艇試圖抓住這個物體,但失敗了,氫彈滑向了更深處。三周後,一艘早期型號的遠端遙控潛水器重新找到了這顆氫彈,但卻不小心將自身與這顆氫彈纏在了一起。冒著巨大的風險,遙控人員操縱著潛水器及纏繞其上的氫彈一起返回了海面。

1966年4月8日,美國海軍的水兵正在檢查從帕洛馬雷斯外海回收的氫彈。在「帕洛馬雷斯事件」發生兩年後,克雷文團隊再次套用貝葉斯定理找到了另一件遺失的物品——美國海軍的「天蠍」號核潛艇。這艘潛艇約在1968年5月21日前後沈沒在了亞速爾群島外海,艇上人員全部遇難。再一次地,貝葉斯定理這一「數學魔法」向世人證實了其巨大的威力。不過,與上次找氫彈時的「眼見為實」不同,這次「找潛艇」是以一種「耳聽為實」的方式證實的:水下聽音器記錄到了潛艇被壓碎的聲音,因為這艘潛艇的下潛深度超過了它所能承受的極限。

沈在海底的「天蠍」號核潛艇的殘骸。
有用的「魔法」
在接下來的幾十年裏,克雷文的這種「數學魔法」一次又一次地證明了自己。例如,2009年,從裏約熱內盧飛往巴黎的法航447號航班在大西洋中部墜毀,墜毀處所在的海底距離海面有3000公尺之多。法國調查人員搜查了兩年都沒有找到殘骸。
最終,法國調查人員求助於美國密特隆咨詢公司。密特隆公司將克雷文的方法套用於當時的整個搜尋工作,並分別就事件、場景和位置計算了機率。密特隆公司的分析師獲取了有關飛行動力學、飛機效能、當地風和洋流的數據,並分別對其計算了機率。然後,他們用之前獲得的法航447號航班的搜尋數據重復了這一步驟,並使用貝葉斯定理來更新他們對墜機發生位置的猜測。不出所料,新的機率將調查人員指引到了之前忽略的位置上。一周之後,搜尋小組從水深約4000公尺的海底回收了飛機的黑匣子。

打撈出水的法航447號航班的殘骸。饒是如此,基於貝葉斯定理的搜尋需要至少提供一些「較好」的數據才能套用。以目前已終止尋找的馬航370號航班為例,由於缺少數據,因此存在各種可能性——也就是說,幾乎任何情況都有可能發生,可我們總不能真的認為是外星人綁架或黑洞吸引導致的吧!在印度洋這片世界上最知之甚少的海域中,沒有目擊者,且幾乎沒有碎片和較確定的搜尋區域,在這種情況下,恐怕就連克雷文這樣的數學「神童」也無從下手。但是我們相信,五十多年前遺失在帕洛馬雷斯外海的那顆氫彈曾被很多人認為是找不到的,但最終憑借數學這一強大的科學工具而被找到了,那麽隨著機率論等數學科學的發展,人們終有一天也會解開包括馬航370號航班在內的諸多「失蹤之謎」。











