位置≠位姿
很多初次接觸機械臂的人都容易範的概念性錯誤,就是用「位置」代替「位姿」,簡單地認為給機械臂一組{x,y,z}座標就可以讓機械臂運動到指定位置,而對於機械臂更為重要的概念「姿態」卻被忽略了。
「姿態」其實在航空領域早就有成熟套用了。航展中飛機特技表演,有一個非常經典的動作叫「雙機對貼飛行」。兩架飛機只能使用這種姿態貼腹飛行,如果飛機的姿態(橫滾角)變化,就可能導致特技表演立馬變成災難現場。

真正接觸機械臂就會發現,要讓機械臂運動必須給定目標位置和姿態,簡稱「位姿」。
位姿怎麽表示呢?
在三維空間中,位置用{x,y,z}表示笛卡爾座標系的一個點表示。姿態可以用: 正交旋轉矩陣、固定角、歐拉角、等效軸角、單位四元數 。
正交旋轉矩陣
原點相同的兩個座標系,可以透過正交旋轉矩陣變換得到。
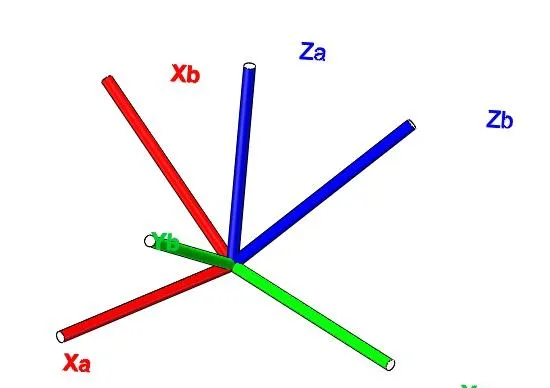
座標系{B}的三個軸可以表示為相對參考座標系{A}中的3個單位向量:
{_{B}^{A}R}=[\hat{^{A}X_{B}},\hat{^{A}Y_{B}},\hat{^{A}Z_{B}}]
每個單位向量又可以用座標系{A}的三個軸上的投影分量(即,點積)來表示:
\hat{^{A}X_{B}} = \left[\begin{array} \\\hat{^{}X_{B}}\cdot\hat{^{}X_{A}} \\\hat{^{}X_{B}}\cdot\hat{^{}Y_{A}} \\\hat{^{}X_{B}}\cdot\hat{^{}Z_{A}} \end{array}\right]
所以組成一個3x3的矩陣:
{_{B}^{A}R}=\left[\begin{array}{c} \begin{array}{ccc} \hat{^{}X_{B}}\cdot\hat{^{}X_{A}} & \hat{^{}Y_{B}}\cdot\hat{^{}X_{A}} & \hat{^{}Z_{B}}\cdot\hat{^{}X_{A}} \\ \hat{^{}X_{B}}\cdot\hat{^{}Y_{A}} & \hat{^{}Y_{B}}\cdot\hat{^{}Y_{A}} & \hat{^{}Z_{B}}\cdot\hat{^{}Y_{A}}\\ \hat{^{}X_{B}}\cdot\hat{^{}Z_{A}} & \hat{^{}Y_{B}}\cdot\hat{^{}Z_{A}} & \hat{^{}Z_{B}}\cdot\hat{^{}Z_{A}} \end{array}\end{array}\right]
雖然旋轉矩陣看起來有9個數值,但實際上由於單位正交矩陣的約束條件,其實只需要3個參量就可以表達。
固定角
每次旋轉都是繞固定參考座標系{A}的軸 。讓{A},{B}兩個座標系重合,先將{B}繞{A}座標系的X軸旋轉 \gamma 角,再繞{A}座標系的Y軸旋轉 \beta 角,最後繞{A}座標系的Z軸旋轉 \alpha 角。
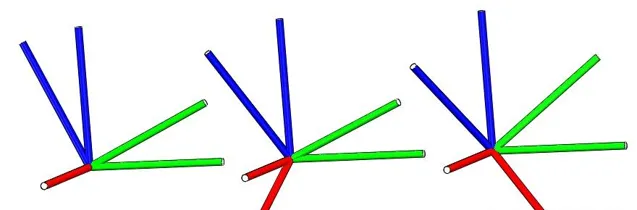
三次旋轉可以分別看成一個旋轉矩陣,最終座標標{B}的姿態可表示為
_{B}^{A}R_{XYZ}(\gamma,\beta,\alpha) = R_{Z}(\alpha)R_{Y}(\beta)R_{X}(\gamma)\\=\left[\begin{array}{c} \begin{array}{ccc} c\alpha & -s\alpha & 0\\ s\alpha & c\alpha & 0\\ 0 & 0 & 1 \end{array}\end{array}\right]\left[\begin{array}{c} \begin{array}{ccc} c\beta & 0 & s\beta\\ 0 & 1 & 0\\ -s\beta & 0 & c\beta \end{array}\end{array}\right]\left[\begin{array}{c} \begin{array}{ccc} 1 & 0 & 0\\ 0 & c\gamma & -s\gamma\\ 0 & s\gamma & c\gamma \end{array}\end{array}\right]
!註意公式裏三個旋轉矩陣的順序是從右到左,將其看作旋轉算子。最終求得
_{B}^{A}R_{XYZ}(\gamma,\beta,\alpha) =\left[\begin{array}{c} \begin{array}{ccc} c\alpha c\beta & c\alpha s\beta s\gamma-s\alpha c\gamma & c\alpha s\beta c\gamma+s\alpha s\gamma\\ s\alpha c\beta & s\alpha s\beta s\gamma+c\alpha c\gamma & s\alpha s\beta c\gamma-c\alpha s\gamma\\ -s\beta & c\beta s\gamma & c\beta c\gamma \end{array}\end{array}\right]
歐拉角
每次都繞運動座標系{B}的各軸旋轉,而不是繞固定座標系{A}的各軸旋轉。
歐拉旋轉定理 :任何兩個獨立的正交座標系都可以透過一系列(不超過3次)相對於座標軸的旋轉聯系起來,但其中連續的兩次旋轉不能繞同一軸線。讓{A},{B}兩個座標系重合,先將{B}繞{B}座標系的Z軸旋轉 \alpha 角,再繞{B}座標系的Y軸旋轉 \beta 角,最後繞{B}座標系的X軸旋轉 \gamma 角。
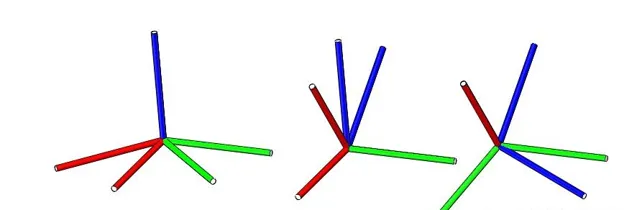
註意每次旋轉所繞的軸都取決於上次的旋轉 。由於這個原因歐拉角的旋轉矩陣按實際的旋轉順序來:
_{B}^{A}R_{Z^{'}Y^{'}X^{'}} = R_{Z}(\alpha)R_{Y}(\beta)R_{X}(\gamma)\\=\left[\begin{array}{c} \begin{array}{ccc} c\alpha & -s\alpha & 0\\ s\alpha & c\alpha & 0\\ 0 & 0 & 1 \end{array}\end{array}\right]\left[\begin{array}{c} \begin{array}{ccc} c\beta & 0 & s\beta\\ 0 & 1 & 0\\ -s\beta & 0 & c\beta \end{array}\end{array}\right]\left[\begin{array}{c} \begin{array}{ccc} 1 & 0 & 0\\ 0 & c\gamma & -s\gamma\\ 0 & s\gamma & c\gamma \end{array}\end{array}\right]
最終求得
_{B}^{A}R_{Z^{'}Y^{'}X^{'}} =\left[\begin{array}{c} \begin{array}{ccc} c\alpha c\beta & c\alpha s\beta s\gamma-s\alpha c\gamma & c\alpha s\beta c\gamma+s\alpha s\gamma\\ s\alpha c\beta & s\alpha s\beta s\gamma+c\alpha c\gamma & s\alpha s\beta c\gamma-c\alpha s\gamma\\ -s\beta & c\beta s\gamma & c\beta c\gamma \end{array}\end{array}\right]
可以看出,這個結果與前面固定角的一樣,實際上: 三次繞固定軸旋轉的得到的姿態和以相反順序繞運動軸旋轉的得到的姿態相同。
另外,固定角、歐拉角各有12種不同的旋轉順序,這24種旋轉方式表示的姿態,都屬於 角座標系表示法 。這種表示法有一個 萬向鎖 的問題,這篇文章講得比較清楚形象。
等效軸角
對於空間中兩個任意姿態的座標系,總可以在空間裏找到某個軸,使其中一個座標系繞該軸旋轉一個角度就能與另一個座標系姿態重合。軸角法,就是用一個軸(向量)和一個繞此向量旋轉的角度 \theta 來表示姿態。首先將座標{B}和一個已知參考座標系{A}重合。將{B}繞向量 \hat{^{A}K} 按右手定則旋轉 \theta 角。註意,兩個座標系原點重合,而且原點必須在旋轉軸上。向量表示為:
\hat{_{}^{A}K}=\left[ k_{x},k_{y},k_{z} \right]^{T}
等效旋轉矩陣為:
_{B}^{A}R_{K}(\theta) =\left[\begin{array}{c} \begin{array}{ccc} k_{x} k_{x} v\theta+c\theta& k_{x} k_{y} v\theta-k_{z}s\theta & k_{x} k_{z} v\theta+k_{y}s\theta\\k_{x} k_{y} v\theta+k_{z}s\theta & k_{y} k_{y} v\theta+c\theta & k_{y} k_{z} v\theta-k_{x}s\theta\\ k_{x} k_{z} v\theta-k_{y}s\theta & k_{y} k_{z} v\theta+k_{x}s\theta & k_{z} k_{z} v\theta+c\theta \end{array}\end{array}\right]
軸角法實際上只需要3個參量(軸2個,角1個),軸表面上是需要3個參量,但實際上空間中的方向只需要2個獨立的單位向量表示,第三個元素可以透過公式:
v3=\sqrt{1-v_{1}^{2}-v_{2}^{2}}
計算出來。軸角法也有使用限制,就是當轉動角為0或180時,軸無法確定。
單位四元數
如果說前面的幾種姿態表示法都還算好理解的話,單位四元數可能有點難度,不直觀是其特點。其優點:容易計算,表示姿態沒有奇異點,完全蓋過缺點。在ROS的MoveIt中就是使用單位四元數來表示姿態。四無數表示為:
\mathring{q} =s<v_{1},v_{2},v_{3}>
下面這個鏈結提供了四元數的視覺化界面,值得一試:
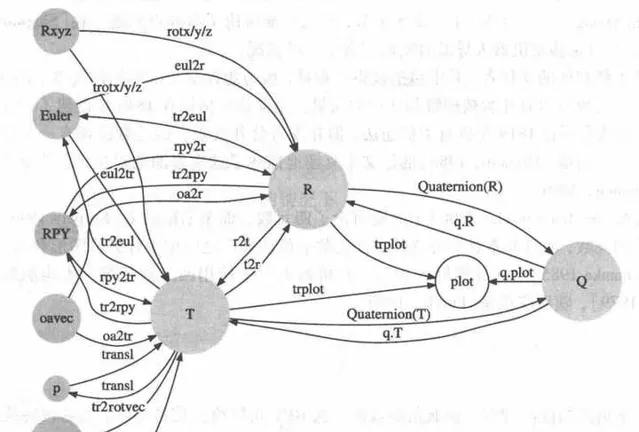
Robotics ToolBox in Matlab
理解姿態是機器人工程師的基礎,一大堆公式和參數看起來非常不直觀。這裏吐血推薦參考書:
本書作者Peter Corke同時也是Robotics ToolBox的開發者。該工具包中,將基礎的位姿旋轉都進行了函式實作,相互之間的轉換關系如下,在matlab中使用這些函式可迅速得到數值計算結果,還可使用trplot繪制座標系,以及tranimate制作旋轉動畫,幫助迅速理解各位姿態表示法。