剛好上課的講義上講了這個例子:

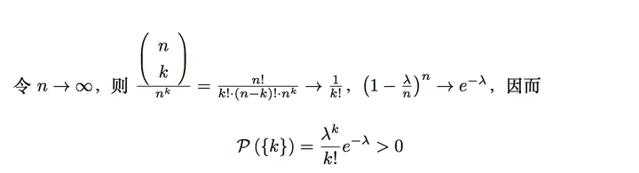
這裏有這麽幾個潛在的假設:
- 每個小區間段是否有客人到達是獨立的
- 每個小區間段客人到達的機率反比於n
這種情況下,根據上面的推理,到達人數就滿足卜瓦松分布了。
對於編程好的人來說,理解為什麽會這樣最好的辦法是做個模擬。不妨按照上面的辦法,取一個比較大的n,產生二項分布,再求和,重復上面步驟1000次,看看分布是怎樣的。可以調整一下n的大小比較一下,看看二項分布是不是趨向於卜瓦松分布。
上面只是模擬,如果是要生成卜瓦松分布隨機數的話,可以直接用分布函式。除了分布函式之外,還有更好的辦法。
如果在一個單位時間內平均到達的人數為\lambda ,那麽t時間內平均到達人數就是\lambda t ,那麽在t時間內沒有人到達的機率為P(\{0\})=e^{-\lambda t}=P({T>t}) ,也就是說兩次到達之間的等待時間服從指數分布。
嗯,所以給定到達率\lambda 和一個時間T,可以不停的產生指數分布t,知道這些t的和大於T了,產生了多少次指數分布就記這個次數,一定服從卜瓦松分布。至於如何產生指數分布,不用我寫了吧。。。










