先上暫時的結論:車能否撞到人,取決於車寬,車與人的極限速度之間的比值,以及車與地面摩擦系數。如果用現實數據,且人沒倒黴到一開始就站在車的近死區,車是撞不到人的。
感謝 @蔡羽 的評論。車追人的最佳策略不是將速度飆到上限,而是將速度開到只比人快一點點。這時候車能保證線上速度比人快的情況下獲得最大的機動性。
另外看到評論區以及後面答案裏一堆人在扯漂移,我覺得有必要澄清一件事,那就是,我下面的推導沒有任何地方說車不能漂移。 之所以用的是靜摩擦系數是因為靜摩擦力能提供的加速度是地面能提供給車的加速度的 上限 ,即使是漂移,車的加速度也不會突破這個上限。
對那些認為車漂移的機動效能突破我說的情況的人,我要抱歉。因為我沒在答案前面解釋的足夠清楚。
推導過程略復雜,高中物理加上一點點極座標知識即可看懂,後面的解方程式步驟用到了求導,但是不影響前面對問題的理解。
首先是假設:
1.車與人分別有上限速度V1和V2,且V1>V2.車與人的機動性受制於抓地能力,(即最大加速度為G*f,f為重力加速度)。
2.車和人都會采取最優的策略。
為了方便分析問題,引入一下幾個概念:極限拐線,盲區,逃逸線,逃逸區,危險區。如圖1所示:
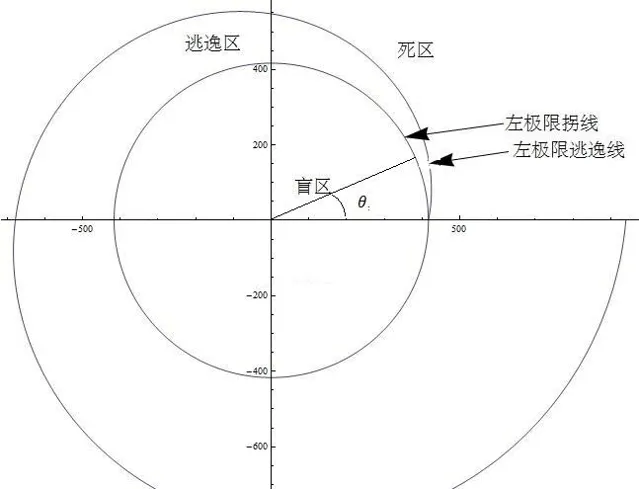
極限拐線:車以恒定速度V1全力左拐(右拐)的軌跡線。顯然這是一個與車行進方向相切,切點為左前輪(右前輪)的圓。半徑根據向心加速度公式為V1^2/(f g)。
盲區:極限拐線包住的區域。
逃逸區:人不在盲區內時,在車撞到人之前,以速度V2能逃進盲區內的區域。
極限逃逸線:逃逸區的外邊界。顯然,逃進盲區的最優線指向車盲區的圓心,逃逸線上任意點朝極限拐線投影路徑長度為
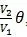
,所以逃逸線是一段阿基米德螺旋線。
死區:盲區、逃逸區外的區域。
如果人在死區,車有能力保證車與人的線距離以及車行進方向與人之間的夾角都在縮小。如果車能夠把人一直釘選在死區,就可以撞到人,註意這裏有一個限定詞"一直"。反之,只要人有任何機會脫離死區進入逃逸區,車就撞不到人。
首先畫出考慮到車寬的盲區、死區、逃逸區分布。見圖2
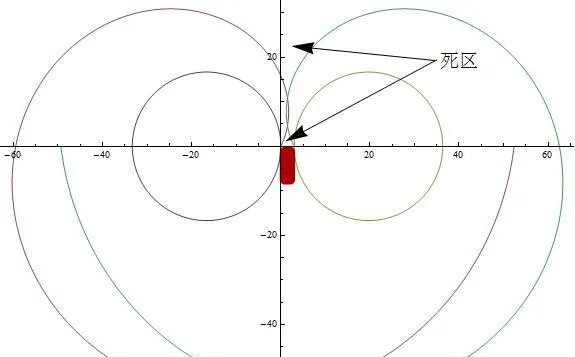
可以發現,死區不一定是連通的,只有死區能夠連通地從車前延伸到無窮遠時,車才能保證能夠釘選人並撞到人,否則在車沖向人,人進入逃逸區的瞬間,人可以采取策略逃離進入盲區。死區的環通度它取決於車寬L、V1 ,V2,f,g 。
為了更方便的理解死區,逃逸區劃分的內在邏輯,我再增加一些描述。首先,車為了能撞到人,必須要保證兩個條件:1.線速度必須比人快,這個很好理解。2.角速度(質心速度方向改變的速度)必須要足夠快,或者說,必須能釘選住人。但是由於如果人垂直於人車連線方向全力奔跑,人離車越近,相對於車的角速度越快,直至正無窮,所以人離車近到一定距離車是無論如何都不能釘選住人的。這時車必須要保證在人脫離釘選前能撞到人。遠死區就是車能保證一直釘選人並追到人的區域。近死區是人在被車追上之前來不及擺脫釘選的區域,逃逸區是人相對於車的角速度大於車最大轉彎角速度的區域。
當然開局時,人不會倒黴到直接出現在近死區,那樣沒法玩。同時,車總能開全力甩開人到足夠遠處調整方向釘選人到遠死區。
考慮死區處於聯通與不連通的臨界狀態,左右兩側的逃逸線應該是相切的。切點的斜率在此處為正無窮。即逃逸線方程式(x(theta),y(theta)) 在切點處滿足dx/d theta =0.即可以求出切點座標,其橫座標為臨界車寬的一半。
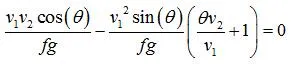
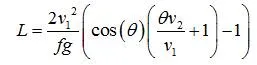
該方程式組是個超越方程式,需要用數值求解方法。
在這裏取v1=60m/s,v2=10m/s,g=10m/s^2,f=0.6,解得L=16m遠超過車寬。
如果取v1=10m/s,v2=10m/s,g=10m/s^2,f=0.6,解得L=10m。車在保證能追到人的最小速度(最大機動)下,需要的車寬仍然遠大於實際車寬。所以仍然撞不到人。
事實上,如果把L看做車速v1的函式,畫出L(v1)在車變速範圍內的變化趨勢。就可以看到,車想保證能撞到人需要的車寬是隨速度增加而單調增加的。












