惊呆了,这不是一道小学数学的题目吗?题目如果是 1+0.9+0.09+0.009+0.0009... 和 2 比较那还差不多,而竟然是 1+0.1+0.01+0.001+0.0001...,就是 1.1111111111... 啊,也太夸张了吧,1.2、1.1111111112、1.3、1.4、1.5 都没到,怎么可能到达 2。看来得给题主补补小学数学了。 请翻开人教版数学四年级下册课本 35 页和 41 页,好好复习复习。
① 小数的表示
打开 35 页(见图1),「做一做」中习题看到没,这就是小数各数位组成的概念,对于题目的:
1+0.1+0.01+0.001+0.0001...
就是1个一,1个十分之一,1个百分之一,1个千分之一,1个万分之一...的和,这正是无限小数各数位的组成,即:
1.\dot{1}=1.111111... =1+0.1+0.01+0.001...
显然,这是一个 循环小数 。 1.\dot{1} 和 2 谁更大呢,也就是 1.1111111111... 和 2 比较谁大谁小,你会判断了吗?
② 小数的大小比较
方法一(直接比较):
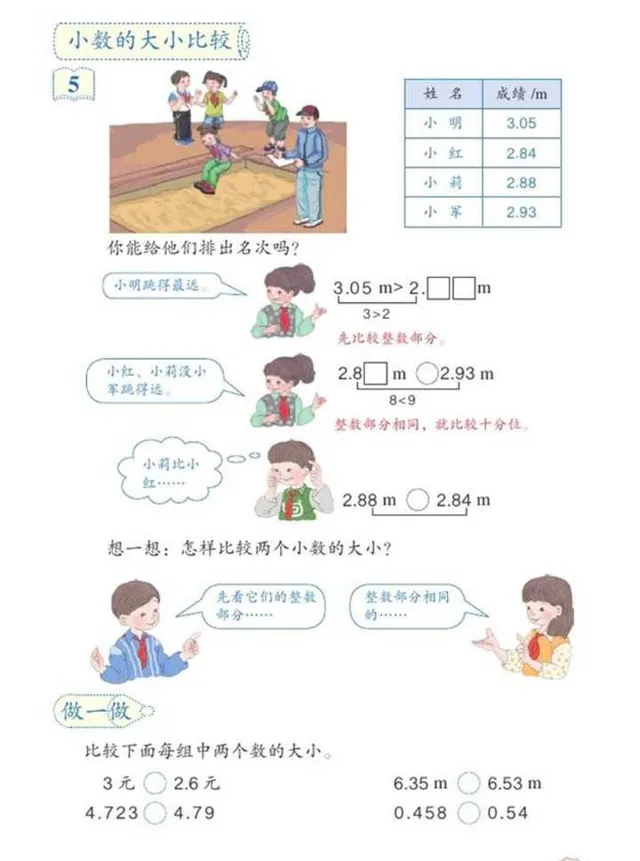
翻到 41 页(见图2),复习怎么比较小数大小 ,先比较整数部分,整数部分相同就比较十分位,十分位相同就比较百分位,依此类推。
题目要比较1.\dot{1} 和 2 的大小关系, 显然整数部分 1 比 2 要小,而且十分位的数字 1 比 9 小 [注:因为1.111...为循环小数,我们要再判断此小数下一位是不是数字9],故 1.\dot{1} < 2。
我们还可以使用小数性质和数字大小关系来 更严格地证明以上大小关系 :
由 0.0\dot{1}\leq0.1, 得 1.\dot{1}=1.1+0.0\dot{1}\leq1.1+0.1=1.2<2。
练习题:我们已知圆周率\pi 的具体数值为3.1415926... ,那么3.1415926... < 4 和1.\dot{1} < 2 比较的形式一样吗?你能说出3.1415926... 和4 之间的一个数字吗?如何用上面的证明方法证明3.1415926... < 4 (大家动手试一试)?
方法二(化成分数比较):
那万一碰到类似 0.\dot{9} 和 1 比较的情况呢?
别急,请打开人教版五年级下册课本第 77 页(见图3), 复习怎么将小数转为分数,然后再比较大小。
我们继续拿 1.\dot{1} 和 2 比较作例子说明:
由\frac{1}{9}=0.\dot{1} ,得 1.\dot{1}=1+\frac{1}{9}=\frac{10}{9}<2,
即 1+0.1+0.01+0.001+0.0001...<2。
练习题:0.\dot{9} 如何转化为分数和 1 比较呢?


③ 拓展内容 (小学超纲知识,可跳过,若感兴趣可进一步钻研)
(1)如何严谨证明 0.\dot{9} 和 1 相等
上面提到的用分数论证 0.\dot{9} 和 1 相等的证明方法是对的吗?有没有更严谨的证明方法呢?请参见知乎上已有的详细解答:为什么 0.9 的循环等于 1?,如何严谨地证明 0.9999…=1?。这里不再赘述。
注:数学证明各有不同的严谨性、背景假设和目标受众。对于非数学研究人员来说,将 0.\dot{9} 转化为分数相乘等于1的形式,或将整体看作一个未知变量乘10之后求差得到未知变量为1的证明形式,均是正确的证明方法;而对于基础数学研究来说,对 0.\dot{9} = 1 最严谨的论证则需要用到实数理论。这些论证形式在奥数教材或数学期刊中都有给出过, 维基词条上更是有词条 「0.999...」( https://en.wikipedia.org/wiki/0.999... ) , 从最简单到最复杂的近十种证明,都全部列出来,本词条上也强调这些证明都是正确的,只是严谨性和受众目标各不同而已 。法国数学家 Jean-Paul Delahaye 也发表过文章【0.999...=1?】(0.999...= 1?),系统性地介绍了从初等数学到高等数学的各种论证形式。
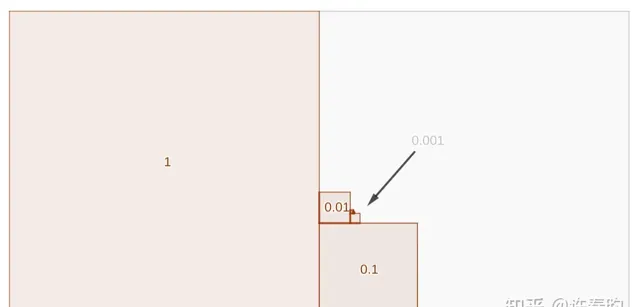
(2)用图形直观表示 1.\dot{1}
如图4所示,最大的正方形面积为单位1,小一点是0.1(边长等于单位1对应正方形边长的 \frac{1}{\sqrt{10}} ),再小一点的是0.01(边长等于0.1对应正方形边长的 \frac{1}{\sqrt{10}} ),依次画下去, 全部粉红色部分就代表小数 1.\dot{1} 的大小 。
白色部分则是第二个单位1的正方形剩下的空间,从直观上看 1.\dot{1} 比 2 小得多,而且越到后面的正方形越挤到下面箭头位置的角落中,1.\dot{1} 也无法收敛于 2 ,毕竟中间还有 1.112,1.12,1.2,1.\dot{2},1.\dot{9} 等等数字。