位置≠位姿
很多初次接触机械臂的人都容易范的概念性错误,就是用「位置」代替「位姿」,简单地认为给机械臂一组{x,y,z}坐标就可以让机械臂运动到指定位置,而对于机械臂更为重要的概念「姿态」却被忽略了。
「姿态」其实在航空领域早就有成熟应用了。航展中飞机特技表演,有一个非常经典的动作叫「双机对贴飞行」。两架飞机只能使用这种姿态贴腹飞行,如果飞机的姿态(横滚角)变化,就可能导致特技表演立马变成灾难现场。

真正接触机械臂就会发现,要让机械臂运动必须给定目标位置和姿态,简称「位姿」。
位姿怎么表示呢?
在三维空间中,位置用{x,y,z}表示笛卡尔坐标系的一个点表示。姿态可以用: 正交旋转矩阵、固定角、欧拉角、等效轴角、单位四元数 。
正交旋转矩阵
原点相同的两个坐标系,可以通过正交旋转矩阵变换得到。
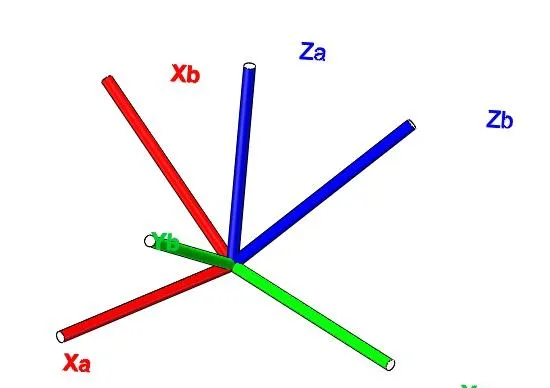
坐标系{B}的三个轴可以表示为相对参考坐标系{A}中的3个单位向量:
{_{B}^{A}R}=[\hat{^{A}X_{B}},\hat{^{A}Y_{B}},\hat{^{A}Z_{B}}]
每个单位向量又可以用坐标系{A}的三个轴上的投影分量(即,点积)来表示:
\hat{^{A}X_{B}} = \left[\begin{array} \\\hat{^{}X_{B}}\cdot\hat{^{}X_{A}} \\\hat{^{}X_{B}}\cdot\hat{^{}Y_{A}} \\\hat{^{}X_{B}}\cdot\hat{^{}Z_{A}} \end{array}\right]
所以组成一个3x3的矩阵:
{_{B}^{A}R}=\left[\begin{array}{c} \begin{array}{ccc} \hat{^{}X_{B}}\cdot\hat{^{}X_{A}} & \hat{^{}Y_{B}}\cdot\hat{^{}X_{A}} & \hat{^{}Z_{B}}\cdot\hat{^{}X_{A}} \\ \hat{^{}X_{B}}\cdot\hat{^{}Y_{A}} & \hat{^{}Y_{B}}\cdot\hat{^{}Y_{A}} & \hat{^{}Z_{B}}\cdot\hat{^{}Y_{A}}\\ \hat{^{}X_{B}}\cdot\hat{^{}Z_{A}} & \hat{^{}Y_{B}}\cdot\hat{^{}Z_{A}} & \hat{^{}Z_{B}}\cdot\hat{^{}Z_{A}} \end{array}\end{array}\right]
虽然旋转矩阵看起来有9个数值,但实际上由于单位正交矩阵的约束条件,其实只需要3个参量就可以表达。
固定角
每次旋转都是绕固定参考坐标系{A}的轴 。让{A},{B}两个坐标系重合,先将{B}绕{A}坐标系的X轴旋转 \gamma 角,再绕{A}坐标系的Y轴旋转 \beta 角,最后绕{A}坐标系的Z轴旋转 \alpha 角。
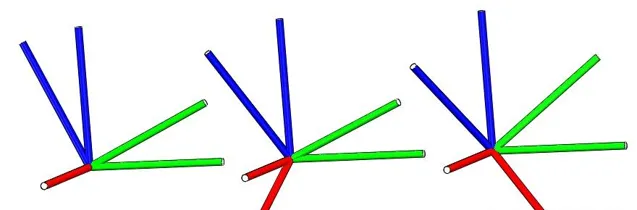
三次旋转可以分别看成一个旋转矩阵,最终坐标标{B}的姿态可表示为
_{B}^{A}R_{XYZ}(\gamma,\beta,\alpha) = R_{Z}(\alpha)R_{Y}(\beta)R_{X}(\gamma)\\=\left[\begin{array}{c} \begin{array}{ccc} c\alpha & -s\alpha & 0\\ s\alpha & c\alpha & 0\\ 0 & 0 & 1 \end{array}\end{array}\right]\left[\begin{array}{c} \begin{array}{ccc} c\beta & 0 & s\beta\\ 0 & 1 & 0\\ -s\beta & 0 & c\beta \end{array}\end{array}\right]\left[\begin{array}{c} \begin{array}{ccc} 1 & 0 & 0\\ 0 & c\gamma & -s\gamma\\ 0 & s\gamma & c\gamma \end{array}\end{array}\right]
!注意公式里三个旋转矩阵的顺序是从右到左,将其看作旋转算子。最终求得
_{B}^{A}R_{XYZ}(\gamma,\beta,\alpha) =\left[\begin{array}{c} \begin{array}{ccc} c\alpha c\beta & c\alpha s\beta s\gamma-s\alpha c\gamma & c\alpha s\beta c\gamma+s\alpha s\gamma\\ s\alpha c\beta & s\alpha s\beta s\gamma+c\alpha c\gamma & s\alpha s\beta c\gamma-c\alpha s\gamma\\ -s\beta & c\beta s\gamma & c\beta c\gamma \end{array}\end{array}\right]
欧拉角
每次都绕运动坐标系{B}的各轴旋转,而不是绕固定坐标系{A}的各轴旋转。
欧拉旋转定理 :任何两个独立的正交坐标系都可以通过一系列(不超过3次)相对于坐标轴的旋转联系起来,但其中连续的两次旋转不能绕同一轴线。让{A},{B}两个坐标系重合,先将{B}绕{B}坐标系的Z轴旋转 \alpha 角,再绕{B}坐标系的Y轴旋转 \beta 角,最后绕{B}坐标系的X轴旋转 \gamma 角。
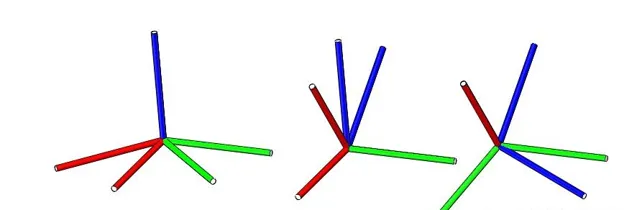
注意每次旋转所绕的轴都取决于上次的旋转 。由于这个原因欧拉角的旋转矩阵按实际的旋转顺序来:
_{B}^{A}R_{Z^{'}Y^{'}X^{'}} = R_{Z}(\alpha)R_{Y}(\beta)R_{X}(\gamma)\\=\left[\begin{array}{c} \begin{array}{ccc} c\alpha & -s\alpha & 0\\ s\alpha & c\alpha & 0\\ 0 & 0 & 1 \end{array}\end{array}\right]\left[\begin{array}{c} \begin{array}{ccc} c\beta & 0 & s\beta\\ 0 & 1 & 0\\ -s\beta & 0 & c\beta \end{array}\end{array}\right]\left[\begin{array}{c} \begin{array}{ccc} 1 & 0 & 0\\ 0 & c\gamma & -s\gamma\\ 0 & s\gamma & c\gamma \end{array}\end{array}\right]
最终求得
_{B}^{A}R_{Z^{'}Y^{'}X^{'}} =\left[\begin{array}{c} \begin{array}{ccc} c\alpha c\beta & c\alpha s\beta s\gamma-s\alpha c\gamma & c\alpha s\beta c\gamma+s\alpha s\gamma\\ s\alpha c\beta & s\alpha s\beta s\gamma+c\alpha c\gamma & s\alpha s\beta c\gamma-c\alpha s\gamma\\ -s\beta & c\beta s\gamma & c\beta c\gamma \end{array}\end{array}\right]
可以看出,这个结果与前面固定角的一样,实际上: 三次绕固定轴旋转的得到的姿态和以相反顺序绕运动轴旋转的得到的姿态相同。
另外,固定角、欧拉角各有12种不同的旋转顺序,这24种旋转方式表示的姿态,都属于 角坐标系表示法 。这种表示法有一个 万向锁 的问题,这篇文章讲得比较清楚形象。
等效轴角
对于空间中两个任意姿态的坐标系,总可以在空间里找到某个轴,使其中一个坐标系绕该轴旋转一个角度就能与另一个坐标系姿态重合。轴角法,就是用一个轴(向量)和一个绕此向量旋转的角度 \theta 来表示姿态。首先将坐标{B}和一个已知参考坐标系{A}重合。将{B}绕矢量 \hat{^{A}K} 按右手定则旋转 \theta 角。注意,两个坐标系原点重合,而且原点必须在旋转轴上。向量表示为:
\hat{_{}^{A}K}=\left[ k_{x},k_{y},k_{z} \right]^{T}
等效旋转矩阵为:
_{B}^{A}R_{K}(\theta) =\left[\begin{array}{c} \begin{array}{ccc} k_{x} k_{x} v\theta+c\theta& k_{x} k_{y} v\theta-k_{z}s\theta & k_{x} k_{z} v\theta+k_{y}s\theta\\k_{x} k_{y} v\theta+k_{z}s\theta & k_{y} k_{y} v\theta+c\theta & k_{y} k_{z} v\theta-k_{x}s\theta\\ k_{x} k_{z} v\theta-k_{y}s\theta & k_{y} k_{z} v\theta+k_{x}s\theta & k_{z} k_{z} v\theta+c\theta \end{array}\end{array}\right]
轴角法实际上只需要3个参量(轴2个,角1个),轴表面上是需要3个参量,但实际上空间中的方向只需要2个独立的单位向量表示,第三个元素可以通过公式:
v3=\sqrt{1-v_{1}^{2}-v_{2}^{2}}
计算出来。轴角法也有使用限制,就是当转动角为0或180时,轴无法确定。
单位四元数
如果说前面的几种姿态表示法都还算好理解的话,单位四元数可能有点难度,不直观是其特点。其优点:容易计算,表示姿态没有奇异点,完全盖过缺点。在ROS的MoveIt中就是使用单位四元数来表示姿态。四无数表示为:
\mathring{q} =s<v_{1},v_{2},v_{3}>
下面这个链结提供了四元数的可视化界面,值得一试:
Robotics ToolBox in Matlab
理解姿态是机器人工程师的基础,一大堆公式和参数看起来非常不直观。这里吐血推荐参考书:
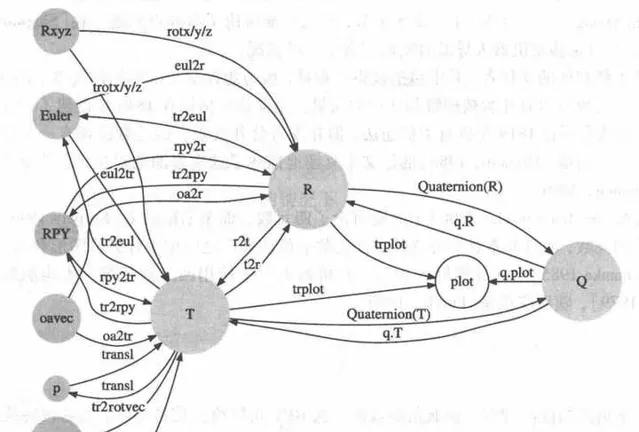
本书作者Peter Corke同时也是Robotics ToolBox的开发者。该工具包中,将基础的位姿旋转都进行了函数实现,相互之间的转换关系如下,在matlab中使用这些函数可迅速得到数值计算结果,还可使用trplot绘制坐标系,以及tranimate制作旋转动画,帮助迅速理解各位姿态表示法。