过去十年中航空航天领域最重要的科学进展是SpaceX的工程师在2012年发表的论文"Lossless Convexification of Nonconvex Control Bound and Pointing Constraints of the Soft Landing Optimal Control Problem"(对最优软着陆问题中非凸的控制约束和朝向约束进行无损凸化),正是这篇论文中讨论的技术点让可回收火箭成为可能。从这篇论文我们可以思考并理解到很多重要的科研、人才培养的问题。
最优软着陆问题介绍
「过去十年中航空航天领域最重要的科学进展」这个评价是我的博士导师Zachary Manchester做出的。由于Zac的博士导师Mason Peck曾担任过NASA的首席技术专家,且Zac自己在NASA Ames Center工作过一段时间,所以这个评价非常令人信服。我们简单科普一下这篇论文的内容,若要详细理解论文的基本技术细节需要首先通读【Numerical Optimization】和【Convex Optimization】两本教科书,如果要进一步看懂论文所有的证明,还需要深入学习最优控制理论。
论文探讨的是「最优软着陆问题」(Soft Landing Optimal Control Problem)。在人类历史上的地外行星探测任务中,探测器着陆不是一件非常困难的事情,但是对于可回收火箭来说,软着陆的难度极大。以往人类只在月球和火星进行过软着陆,最常用的方法是在探测器近地面的时候点燃反推发动机减速,比方说嫦娥五号登月就用了这种方式。

由于月球重力低,登月舱相对较轻,反推发动机不需要长时间运行,所以很容易做出推力巨大的发动机来实现这件事。一般反推发动机运行时可产生几倍于火箭重力的推力(推重比),这让登陆器能够在落地前大力出奇迹地把速度降低。
但是可回收火箭回地球软着陆的时候,反推的推力是有限的。一方面地球重力较大,另一方面火箭本身除了主发动机以外不可能再安装额外的反推发动机,因此降落期间的推重比一般在1.2到1.5之间,火箭不能只在降落前十秒钟才开始进行反推,而是要从高空开始就规划一条运动轨迹,持续调整控制发动机的输出,为此,火箭控制器需要在全降落过程中每时每刻实时解算两个带约束的非线性优化问题。

本论文中不仅构造了火箭软着陆的优化问题,并且提出了有严密证明支撑的重构方法,让软着陆优化问题能够在实际火箭上快速求解。下一节我们简单介绍一下论文中对于软着陆优化问题的求解过程,如果不想看太多数学表达式的话可以略过这一节。
重构软着陆的非凸优化问题
软着陆中有两个需要被求解的优化问题是这样的:

这两个问题形式非常类似,在实际中需要一起被求解,问题2的解与问题1的解有关,问题2最后解出的是火箭在全过程中每个时刻应该施加的推力值,如果问题解算得足够快,它就可以被用于一个模型预测控制器中用来生成给发动机的推力输出值。其中第一个问题比较重要,它描述的是:「给定火箭初始的位置( r(0)=r_0 ,速度( \dot{r}(0)=\dot{r}_0 )和燃料质量( m(0)=m_0 ),我们希望求解火箭从开始到时间 t_f 期间的推力函数 T_c(t) ,使得火箭在时间 t_f 后降落到海平面高度( e_1^Tr(t_f)=0 ),降落时速度恰好为0( \dot{r}(t_f)=0 ),且剩余燃料量大于一定值( m_f )。在此期间,火箭的位置、姿态和燃料的消耗量必须满足运动状态方程(4),位置和姿态必须处于一定的空间内(5)。最重要的是,火箭输出的推力 T_c(t) 必须满足两个约束条件(6)」。虽然看起来复杂,但是这可以化成标准的有约束非线性优化形式,并且使用成熟的非线性优化工具比如IPOPT求解。读者可以先不用关心每个公式具体的意义,可以只对比上述问题和下面这个构造的相似之处。
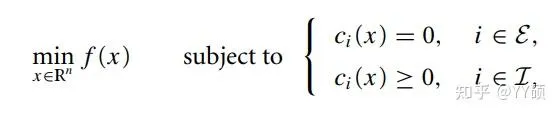
这个问题虽然可以被优化工具求解,但是一直以来被认为没有什么用——因为这个问题是非凸优化问题,求解需要大量的时间,下面我们简单说说凸优化和非凸优化。
世界上有两类有约束的优化问题,一类是凸的,另一类是非凸的。两者的区别是优化问题的变量的可行域是否是凸集。如下图(A)组中两个形状的可行域是凸集,(B)组中两个则是非凸集,凸集的定义是「集合中任两点间的连线上的点仍在集合中的集合」。感性地理解凸与非凸对于优化的影响是,我们现在所掌握的数学工具只允许我们从集合中的某点开始在可行域中通过某些方式连续移动,期望能够寻找到让代价函数最小的一个点。在凸集中,优化过程中点的移动几乎都可以直线移动不受什么限制,而在非凸集中,比如B组中的集合,想要从P1点移动到P2点而不离开集合内部需要走个拐弯,这样「走」并不好用数学语言去描述。因此在非凸集合上的优化大大难于在凸集上的优化。
凸优化和非凸优化的关系很类似计算机科学里面的P与NP问题,P问题有高效求解的算法,可以在短时间内求解,而NP问题没有,通常要计算非常久的时间;NP问题通过巧妙的重新构造有时可以变成P问题,但是没有通用的重构方法。而且,就像我们不知道P是否等于NP一样,我们不知道是不是所有的非凸问题都能够重新构造成凸问题。
软着陆问题是非凸优化的原因是,火箭推力 T_c 的约束条件 0<\rho_1\leq\|T_c(t)\|\leq\rho_2 以及 \hat{n}^TT_c(t)\geq\|T_c(t)\|cos\theta 使得推力的可行域是一个非凸的集合,也就是下图中深蓝色的区域:
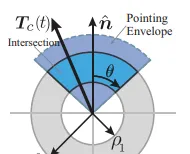
可行域这个环状的结构部分(图中灰色的区域)是由于火箭推力有最大值也有最小值导致的。其他答主有提到Space X的梅林发动机是世界上超一流的高推重比发动机,但是梅林发动机整合到火箭上之后依然只有最多不超过1.5的推重比(别忘了火箭还需要有可伸缩的起落架结构)。因此火箭整体的推力有很低的上限,另外火箭在空中也没法把发动机停下来,所以有推力的下限。推力的上下限带来了非凸的可行域集合。
对于火箭控制,控制问题是凸还是非凸的区别会导致控制器能不能高频对火箭施加控制。SpaceX并没有公开可回收火箭的工程技术细节,根据其他火箭系统推断,我觉得合理的控制频率应该在10Hz以上,因此火箭的飞控计算机必须能够在100ms内解出上述优化问题,然而上述这个非凸优化求解一次需要的时间以秒为单位(在性能较好的桌面计算机上一般需要求解5-10秒钟),远远不足以用来生成高频控制量。
这篇论文中的解法是把推力的约束条件重构成如下形式:
\|T_c(t)\|\leq\Gamma(t) \\ 0 < \rho_1\leq\Gamma(t) \leq \rho_2 \\ \hat{n}^TT_c(t) \geq \cos\theta \ \Gamma(t)
其中 \Gamma(t) 是额外引入的一个待优化变量,这是优化中常用的方式——通过增加优化变量来重构某些约束。在这个问题里 \Gamma(t) 代表推力的上限值。这样重构之后,推力的可行域变成了如下形式的凸集(假设我们研究二维平面内的控制问题,推力只有2维)
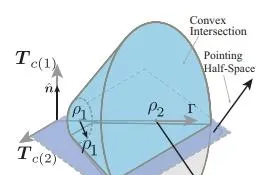
这是一个被切了两刀的圆锥体,满足我们之前所说的凸集的定义。进行重构后,需要被求解的问题1就变成了如下的问题3
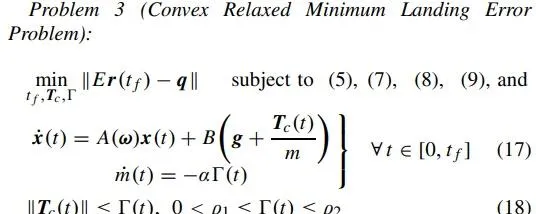
而问题2则可以被重构成下面的问题4,这是一个凸优化问题

这个变形看似简单,但是蕴涵着极丰富的数学原理。为什么这样的重构是等价的呢?换句话说,如何确保重构后的凸优化问题的解也是原来非凸优化问题的解呢?要知道火箭控制中安全至关重要,如果没有十足的理论证明,这样的重构是不可靠的。于是论文中最精华的部分来了——作者们通过极严密的数学推导,证明问题4和问题3的解一定和问题2同问题1等价,证明中需要用到最优控制中的哈密尔顿函数以及庞特里亚金最大化原理。但是惭愧地说,虽然我自认认真学习过最优控制理论,也在数值优化领域实践了两年,能够用各种仿真工具按照论文做出可回收火箭的降落控制器,但是这个证明我暂时还没有完全看懂。如果有读者看懂且能够把详细的步骤写出来,希望有机会可以交流交流。
软着陆优化问题快速求解的意义
上一节中我们简单浏览了论文中将软着陆问题由非凸优化变换成凸优化的过程。在论文的结束语中作者们只是含蓄地讲到"This convexification enables the planetary soft landing problem to be solved optimally by using convex optimization, and is hence amenable to onboard implementation with a priori bounds on the computational complexity and realtime execution time."(这个变换让行星软着陆问题可以作为凸优化问题被求解,因此能够在有计算复杂度限制和实时计算限制的机载计算机上被执行)。通常来说,一个非线性优化问题由非凸优化重构成凸优化之后计算速度可以指数级提升,因此火箭的主控计算机能够以10Hz或者更高的频率计算软着陆过程中火箭需要的推力,从而实现对火箭的模型预测控制。在论文发表后不久的2013年,Space X开始测试名为Grasshopper的火箭,将论文中讨论的优化算法实现在了真火箭上。
随后的故事世人皆知。2013年我刚加入大疆,当时只知道Space X测试Grasshopper时用了大疆的S600六轴飞行器做拍摄,却不知其背后激动人心的数学和优化技术的进展。所以回头再看的话,说这篇论文是「过去十年中航空航天领域最重要的科学进展」并不夸张。我辈生也晚,人类历史上伟大的工程学进展大多只是书中的记载,而如今这「让人类成为星际文明生物」的科技发展,不仅有详实的影像,还有其背后的数学和工程学基础知识可以阅读,实在是一种幸运。
另外这项科研也给有志攀登科学和工程学高峰的研究人员特别是博士生指出了如何进行有价值研究工作的思路:针对一个已经或者接近投入大规模使用的控制系统(火箭),提出一个方法让该系统能够具有新的功能或者显著提高已有的功能(显著提高软着陆的效率),有严密的数学推导证明(由最优控制理论证明凸变换的有效性),能够在实际系统上验证(Space X Grasshopper火箭)。我自己就在自己的研究领域试图寻找这样的工作。
从论文说开去
2013年之后,随着Space X可回收火箭的成功,航空航天和机器人领域的研究人员开始重新看待基于优化的控制算法和轨迹生成算法。几年后波士顿动力也开始展示Atlas机器人使用基于优化的轨迹规划算法进行的跳舞、跑酷等动作。我的导师Zachary Manchester在2012-2013年间在NASA Ames Research Center工作,经历了Space X这一系列开天辟地的壮举,也在NASA内耳濡目染了其中的原理(读者可能注意到Space X和NASA进行了大量的合作,特别是早期的软着陆问题只有NASA在研究,SpaceX获得成功后,NASA体制内的工程师都非常羡慕嫉妒恨),于是他在博士毕业后加入了哈佛教授Scott Kuindersma的实验室做博士后,研究复杂控制系统的非线性优化问题。Scott Kuindersma后来加入了波士顿动力公司,继续在Atlas机器人上研发非线性优化控制器。因此Space X可回收火箭极大促进了各种相关领域的发展。直到今天,非线性优化和模型预测控制成为了当代最优秀的一些机器人和复杂控制系统的主流技术(并不是强化学习),其中依然有丰富的数学和工程学问题可以探索。我认真学习了几年,最近也稍稍小有所得。
2022年,纪录片Return To Space(【重返太空】)上映,这个详细记录Space X从诞生到成功实现载人航天飞行全过程的纪录片非常有意思。我们谈论的这篇论文的通讯作者Lars Blackmore在里面简短出镜,用大众听得懂的语言介绍了一下可回收火箭的原理,结果听起来毫不激动人心,毕竟这项工作的精华是很少有人了解的凸优化。Lars Blackmore的经历很值得说道说道,他是英国人,在剑桥大学读完本科和研究生后,到美国麻省理工学院读完了博士学位,2007年毕业后在NASA喷气推进实验室工作到2011年,主要参与火星软着陆控制,然后加入Space X研究可回收火箭降落至今。可以说是英美两国最好的教育资源一起培养出来的人才。
除了Lars Blackmore以外,Space X在纪录片中出镜的工程师几乎都是「外国人」:Hans Koenigsmann出镜最多,德国人,本科和博士学位均在德国获得。根据美国网友不知何处听来的小道消息我们现在大概知道在Hans Koenigsmann的带领下Space X设计了一套使用3台消费级电脑x86处理器同时运行6个相同的飞控程序的冗余飞控方案——SpaceX使用消费级计算机硬件革命性地改变航天计算机的设计思路是另一个激动人心的话题,我们暂且先按下不表。另外一个出镜的工程师Balachandar Ramamurthy,飞行安全技术总监,则是印度人,在印度获得本科学位。再有一位负责发射的副总裁Kiko Dontchev,看背景是实打实的美国人,本科和研究生都在密西根大学获得,但是他的姓Dontchev是罕见的保加利亚后裔才有的姓氏。
此外,如果有读者注意到——可回收火箭论文的一作Behçet Açıkmese是土耳其人,在土耳其获得本科学位后,继续在美国获得博士学位,通过最优控制理论证明凸化的准确性的数学证明八成是他做出的,这种水平的证明全世界可能只有不到十个人能做出来。最后,众所周知——Space X的创始人Elon Musk是南非人。
所以Space X的成果离不开各个国家汇集到美国的人才的共同努力。太空探索作为人类应用物理学和工程学的最前沿,一定需要人类各个民族共同的参与。因为一些政治悲剧,美国的NASA不能和中国航天机构合作,但是不管美国是搬起石头砸自己的脚也好,霸权主义也好,撇开政治不谈,这个国家对于太空探索这件事情构建了一个从产业链到科研院所组织再到能够吸聚全人类人才的移民体系的全方面社会架构。领导太空探索这件事已经成为了美国构建民族意识的最好媒介之一。因此美国即使排斥和中国的合作,依然能够不断通过从其他国家移民来补全航天的人才梯队。当有志于成为太空探索领导者的中国在当代挑战美国的地位时,人们常常忽略吸聚人才的重要性,这是中国需要学习和提高的地方。
不过我们更希望在未来,任何一个优秀的工程师都能自由地在地球上任何一个航天机构从事科研开发,所有的航天机构都能分工合作,地球上所有的人们都能摒弃国家和种族的纷争,真正地携手走向星际文明时代。











