摘要
近年來,氪金抽卡逐漸演變成為遊戲中相對主流的新型付費模式。一方面,抽卡的以小博大能拉低使用者的付費門檻,且能潛移默化地完成直購付費難以做到的捆綁銷售;另一方面,若抽卡的隨機性不加以控制,也會給相當部份使用者帶來十分糟糕的體驗。
首先,本文從抽獎系統的隨機性設計作為切入點,采用統計學方法分析了完全隨機、直接保底、PRD保底的數據分布規律,得出「可控性大小依次為PRD保底>直接保底>完全隨機」的結論。
然後,本文依次介紹了在感官體驗上具有天然優勢的雙層抽獎模型,繫結商店系統的抽獎積分模型,並且羅列了一些常見動態獎池的數值推導方法。
最後,本文推廣到廣義上的隨機性設計,抽象出可控性隨機的三大指標:隨機振幅、隨機頻次和概率分布,並圍繞這三大指標列舉了一些套用例項。
關鍵詞: 獎池;保底;隨機性;可控性
一、 引言
在大多數遊戲中,抽獎是不可或缺的重要玩法,也是促進玩家消費的主要手段。比起抽獎,雖然直購活動的性價比更高,但是玩家更傾向於選擇能夠「以小博大」的抽獎活動。本文將從數值角度由淺及深地介紹抽獎系統的模型設計,並著重結合【明日方舟】和【原神】進行數據分析。
個人思路:1)先吃透簡化的基礎數值模型,後研究復雜的進階數值模型;
2)性價比是影響玩家經濟決策的主要因素,但不是絕對的;
3)數值設定的切入點是找到直接影響玩家遊戲體驗的統計變量。
二、 最簡抽獎模型
2.1 數值模型
現有一個靜態獎池,每次抽獎均為獨立且相同的隨機事件,每次抽獎的消耗為C,獎品i的中獎機率為Pi,價值為Vi,i=1,2,...,N。
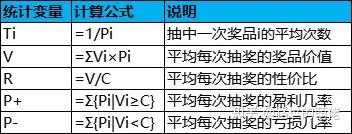
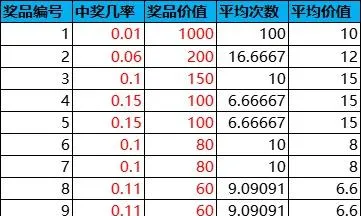
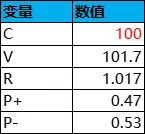
舉個例子,設有一個抽獎活動,共有10種獎品,每次抽獎的消耗為100,每種獎品的中獎機率和價值如下,則根據公式即可計算出每種獎品中獎的平均次數Ti、平均獎品價值V、性價比R、平均每次抽獎的盈利機率P+、虧損機率P-,如下表所示:
2.2 存在問題
1)概率權重(程式)
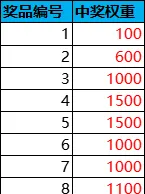
在遊戲中,抽獎活動是會隨時更新的,比如新增一種獎品。若數據配置表直接配置中獎機率,則每次新增獎品時,每種獎品的中獎機率都要重新調整,導致更新維護相對繁瑣。因此,數據配置表一般不是直接配置中獎機率,而是配置成中獎權重。中獎權重Wi和中獎機率Pi的換算關系為Pi=Wi/ΣWj。
上述例子中,每種獎品的中獎權重如下表所示:(填法不唯一,總權重一般控制在10000左右,確保可調空間足夠大)
2)連續中大獎或連續不中大獎的極端情況
玩家參加抽獎活動往往抱著「以小博大」的心理,也就是說,大獎才是玩家的核心關註點。具體而言,實際抽多少次才能抽中大獎,這是玩家參與抽獎活動的核心體驗。
設抽中大獎機率為P*,抽中大獎的平均次數為T*,抽中大獎的實際次數為T。顯然,T*=1/P*,這也是玩家預期抽中大獎次數的參考數值。然而,T*要在大數據支撐下才具有實際意義。玩家抽中大獎的實際次數T和平均次數T*是截然不同的,T<<T*或者T>>T*的兩種極端情況在遊戲中時有發生。

上述例子中,獎品1為大獎,中獎機率P*=0.01,抽中大獎的平均次數T*=1/P*=100,下面給出幾種情況的計算結果:
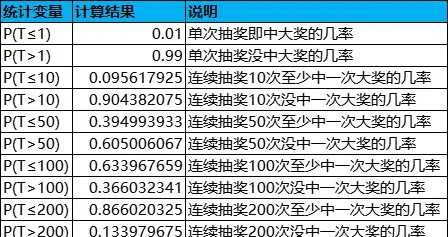
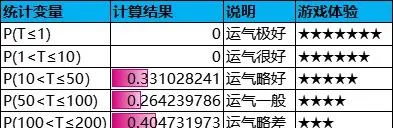
為了更加直觀,把上述情況劃分成互不相交的幾種情況,計算結果如下表所示:
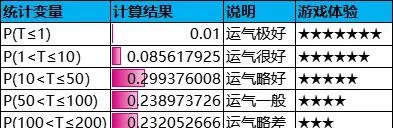
由此可見,即使抽中大獎的平均次數為100,依舊有高達36.6%的機率超過100次才能抽中大獎,甚至出現1.8%的機率超過400次才能抽中大獎;與之相對,也會出現1%的機率單抽即中大獎。
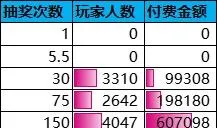
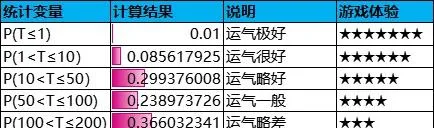
設參與抽獎活動的玩家人數為10000,每個玩家直到抽中一次大獎即停止抽獎,每次抽獎的所需付費金額為1元。根據上述抽獎次數的概率分布,即可計算出各抽獎區間的抽獎次數中位值、玩家人數分布和付費金額分布。
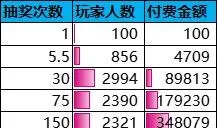
從付費金額的分布來看,超過50%的付費來源於「運氣略差」和「運氣很差」這兩大群體。也就是說,核心付費群體的運氣偏差,抽獎體驗不好。另一方面,運氣不差的玩家人數為3950≈40%,付費金額僅為94622≈9%。這種情況跟前面的核心付費群體恰好形成一種對立反常現象。從長遠來看,這將會導致核心付費群體的逐漸流失,玩家付費習慣趨於小額化,不利於遊戲的可持續發展。
為了杜絕這些極端異常現象,如今市面上很多遊戲的抽獎活動中針對大獎都會加入保底機制,其中卡牌類遊戲尤為明顯。
2.3 實際套用
1)價值相當的獎勵組
比如隨機部位裝備掉落、隨機內容寶石寶箱、隨機同星級角色等等。若獎勵組中同時包含稀有道具和普通道具,則可將稀有道具進行碎片化處理,並改為投放稀有道具碎片。
2)高頻次隨機事件
比如掛機打怪、野外采集、傷害波動等等。
3)非小概率事件
比如低階裝備掉落、普通材料掉落、遊戲幣掉落等等。
三、 保底機制
3.1 直接保底
設A為最小保底次數,B為最大保底次數,0≤A<B,則直接保底的大獎概率分布如下:

記直接保底模型為DR-GT(A, B, P*)。
根據概率論知識,抽中大獎的平均次數T*的計算公式如下:
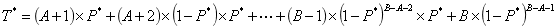
根據代數知識,化簡可得:
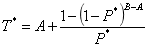
舉個例子,對於直接保底模型DR-GT(10, 200, 0.01),代入公式可得:
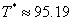
下面直接給出此保底規則下的抽獎次數的概率分布和付費金額的數據表和曲線圖:


對照之前的例子,最顯著的差異就是「T≤10」和「T>200」的兩種極端情況直接被剔除。雖然根絕了抽獎的兩種極端情況,但是由於直接保底的設計過於粗糙,從而帶來一些新的問題。其一是保底規律太明顯,隨機性降低,抽獎體驗趨於平庸;其二是概率分布不平滑,依然有較大概率吃保底。在本例中,P(T=200)=(1-0.01)^(200-10-1)≈14.96%,即吃保底的機率為14.96%,從而導致吃保底玩家的總付費金額達到300000≈31%。也就是說,核心付費群體的抽獎體驗依舊是偏差的。
3.2 PRD保底
設大獎基礎概率為P*,基礎概率次數為A,最大保底次數為B,大獎概率增量為ΔP,1≤A<B,則PRD保底的大獎概率分布如下:

記PRD保底模型為PRD-GT(A, B, P*, ΔP)。其中,最大保底次數B=min{T|P*+(T-A)×ΔP≥1}。
根據概率論知識,抽中大獎的平均次數T*的計算公式如下:
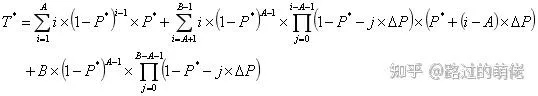
舉個例子,對於PRD保底模型PRD-GT(100, 199, 0.01, 0.01),代入公式(Excel拉表)可得:
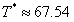
下面直接給出此保底規則下的抽獎次數的概率分布和付費金額的數據表和曲線圖:
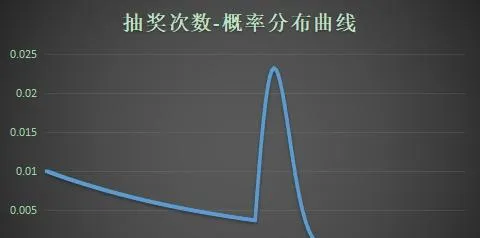
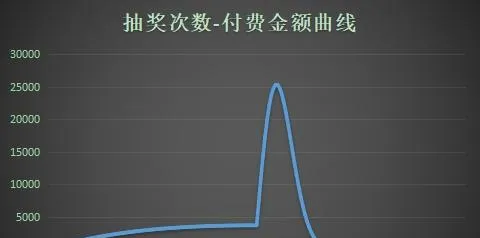
從抽獎次數-概率分布曲線來看,P(T≥130)≈0,即抽中大獎的實際次數幾乎不超過130次,也就幾乎更不可能吃保底了。相較於直接保底,PRD保底規律不太明顯,具有一定的隨機性,抽獎體驗良好。基於這些優點,PRD保底逐漸成為相對主流的抽獎保底規則。
3.3 模擬抽獎
下面我們模擬無保底、直接保底和PRD保底的抽獎情況,並根據樣本統計數據來比較它們之間的差異性。
1)無保底:p*=1/50=0.02
2)直接保底:DR-GT(0, 100, 0.016)
3)PRD保底:PRD-GT(57, 156, 0.01, 0.01)
上述三個抽獎模型都是建立在大獎平均次數T*≈50的前提下,其中,直接保底和PRD保底的數值模型並不唯一。下面是用VBA模擬(詳見 第八章的VBA程式碼附錄 )三種情況200次大獎的抽獎次數分布樣本,並計算出相應的樣本統計量。

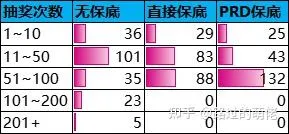
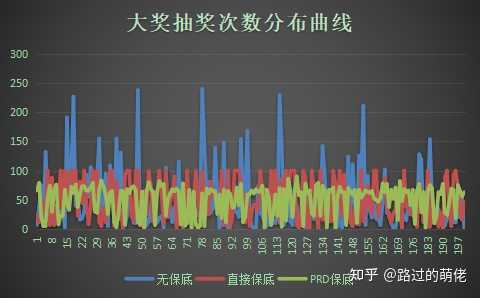
從最小次數來看,由於基礎概率為0.01~0.02,樣本總數為200,三種抽獎模型都出現了一次即中大獎(或連續兩次中大獎)的正常現象;從最大次數來看,無保底的可控性最差,PRD保底的可控性最好,盡管PRD保底的保底次數大於直接保底的最大保底;從平均次數來看,三種抽獎模型都為50左右,原因是三個模型都是建立在T*≈50的基礎上;從極差和標準偏差來看,無保底的數據分布最為混亂,PRD的數據分布最為均勻,這一點從分布曲線圖可以明顯地看出來。
3.4 實際套用
1)直接保底的次級獎勵組
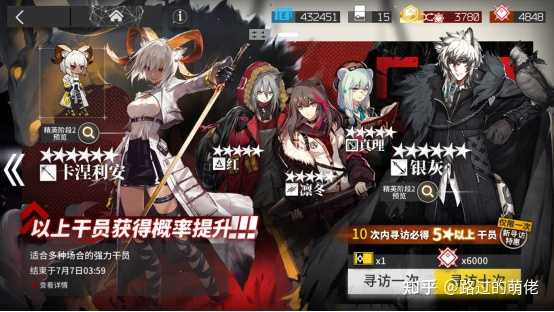
比如【明日方舟】的「10次內尋訪必得5★以上幹員」為直接保底模型DR-GT(0, 10, 0.08)。
2)PRD保底的次級獎勵組
比如【原神】的角色池4星保底為PRD保底模型PRD-GT(8, 10, 0.051, 0.51),武器池4星保底為PRD保底模型PRD-GT(7, 9, 0.06, 0.6)。
3)PRD保底的頂級獎勵組
比如【原神】的角色池5星保底為PRD保底模型PRD-GT(73, 90, 0.006, 0.06),武器池5星保底為PRD保底模型PRD-GT(62, 77, 0.007, 0.07),【明日方舟】的6星保底為PRD保底模型PRD-GT(50, 99, 0.02, 0.02)。
[數據討論] 原神抽卡概率工具表 - 更新n命m精所需抽數/常駐五星類別預測 NGA玩家社區
4)直接保底的up大保底
比如【原神】的角色up池大保底為直接保底模型DR-GT(0, 2, 0.5),武器up池定軌機制為直接保底模型DR-GT(0, 3, 0.375)。這裏說明一下,【原神】抽卡為雙層抽獎模型,第1層決定獲得獎勵的星級,第2層決定該星級下的具體獎勵。大保底和定軌機制是指第2層的up獎勵。
四、 雙層抽獎模型
4.1 數值模型
現有一個靜態獎池,獎池分為兩層,每次抽獎的消耗為C,第1層的第i個獎勵組的中獎機率為Pi,在抽中第i個獎勵組的前提下,第2層的第j個獎品的中獎機率為Pij,價值為Vij,i=1,2,...,N,j=1,2,...,Ni。
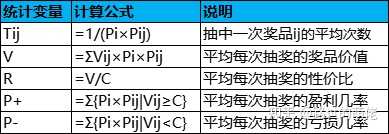
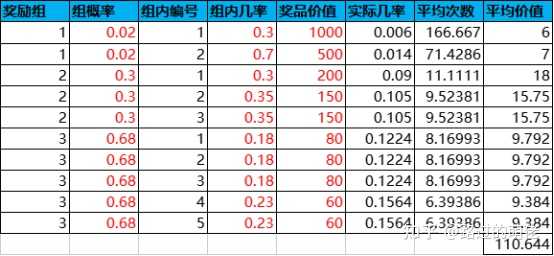
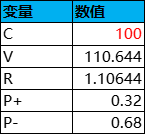
舉個例子,設有一個抽獎活動,共有3個獎勵組(2+3+5),每次抽獎的消耗為100,獎勵的概率和價值如下,則根據公式即可計算出每種獎品中獎的平均次數Tij、平均獎品價值V、性價比R、平均每次抽獎的盈利機率P+、虧損機率P-,如下表所示:
雙層抽獎模型可轉換為最簡抽獎模型;反之,透過對獎品進行分組,最簡抽獎模型也可轉換為雙層抽獎模型。若只看抽獎結果,則雙層抽獎模型近乎等效於最簡抽獎模型。實際上,雙層抽獎模型的意義主要體現於過程而非結果。
4.2 模型優點
1)可賦予雙重抽獎體驗
在邏輯上,雙層抽獎模型可分為兩個階段。第1階段決定哪個獎勵組,而第2階段決定該獎勵組下的哪個獎品。在程式上,一次抽獎過程幾乎是瞬間完成的;在表現上,一次抽獎過程分為抽獎動畫/特效和獎品展示。顯然,抽獎動畫賦予了第1階段的抽獎體驗,而獎品展示賦予了第2階段的抽獎體驗。若遊戲直接給出抽獎結果,則抽獎體驗將會大打折扣。
【明日方舟】的單次抽卡過程為:互動拉鏈(前1/10進度的表現是一樣的,拉開1/10後根據不同星級顯示不同顏色閃光特效)→閃光特效(白/紫/金/彩光對應3/4/5/6星)→卡牌展示(白/灰/金/彩邊對應3/4/5/6星)→星級展示(3/4/5/6星)→幹員展示→獎勵結算;十連抽卡過程為:互動拉鏈(同上)→閃光特效(根據最高星級)→卡牌展示(10個卡牌的星級)→卡牌1星級展示→卡牌1幹員展示→卡牌2星級展示→卡牌2幹員展示→...→卡牌10星級展示→卡牌10幹員展示→獎勵結算。
【原神】的單次抽卡過程為:流星墜落(0-2秒的表現是一樣的,2-6秒根據不同星級顯示不同顏色閃光特效)→閃光特效(藍/紫/金光對應3/4/5星)→角色/武器展示→獎勵結算;十連抽卡過程為:流星墜落(同上)→閃光特效(根據最高星級)→角色/武器1展示→角色/武器2展示→...→角色/武器10展示→獎勵結算。
對比【明日方舟】和【原神】的抽卡過程,前者更為復雜,多了兩個小階段,分別是「卡牌展示」和「星級展示」。對於單抽,這兩個小階段所表現的資訊跟閃光特效是一樣的,可以說是冗余的;對於十連抽,不同於閃光特效只表現最高星級資訊,卡牌展示表現了10個卡牌的星級資訊,星級展示則逐個表現每個卡牌的星級資訊。基於這一差異,【明日方舟】和【原神】的十連抽卡體驗是有區別的,特別是抽到2個以上大獎時的資訊反饋。
在不跳過抽獎動畫的前提下,某玩家在【明日方舟】某次十連抽出3個6星,得到的反饋是「臥槽!出6星了!」→「臥槽!!!竟然出3個6星!」;而在【原神】某次十連抽出3個5星,得到的反饋是「臥槽!出5星了!」→「臥槽!!又一個5星!」→「臥槽!!!又來一個5星!」。 在這種情況下,【明日方舟】的抽獎反饋是爆發式的,【原神】的抽獎反饋是遞進式的。造就這一體驗差異的根本原因是【明日方舟】的「卡牌展示」階段提前表現10個卡牌的星級資訊。抽獎動畫的設計靈感也能在現實生活中找到影子。 以雙色球為例,遊戲的抽獎動畫就對應雙色球的開獎過程,這一過程無疑延長了抽獎體驗。

2)直觀且精細的抽獎概率
一方面,獎勵組的劃分直觀地體現了組內獎品稀有度的性質,獎勵組的機率直觀地體現了組內獎品的獲取難度。另一方面,若單層抽獎概率的精度為r,則雙層抽獎概率的精度為r^2。
五、 抽獎積分
5.1 數值模型
設每次抽獎返還F點積分,積分可用於兌換抽獎券或其它資源(兌換抽獎券的性價比≥其它資源),抽獎券的兌換價格為G點積分,平均抽獎k次即可兌換一張抽獎券,即G=k×F。每次抽獎消耗為C,而每張抽獎券為G點積分,以此作為積分的價值標準,則每點積分的價值為C/G。於是,兌換抽獎券的性價比為C/(G×C/G)=1。
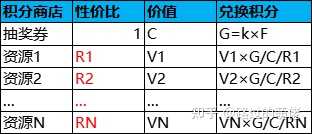
在此模型中,F、k、Ri為設定值,C、Vi為已知值,而商品的兌換積分為匯出值。其中,F是可隨意取的,在盡量小的前提下保證其它推導結果均為整數即可;k取為10左右;Ri則根據具體專案需求自行設定。 為了避免玩家消費的單一化,積分商店的商品會設定每期的購買數量上限,並針對不同檔次的付費玩家,設定不同檔次的商品。 比如,1檔商品的性價比約為2,限購數量較少,零氪黨恰好搬空1檔商品;2檔商品的性價比約為1,限購數量較多,中氪黨可恰好搬空1檔商品+2檔商品;3檔商品的性價比約為0.5,無限購上限,用於消耗重氪黨溢位的剩余積分。
5.2 積分拆解
每次抽獎結果大致可分為兩種情況,即抽到稀有獎勵或抽到普通獎勵。若抽到稀有獎勵,則本次抽獎返還F1點稀有積分;若抽到普通獎勵,則本次抽獎返還F2點普通積分。記抽到稀有獎勵的概率為P*,則抽到普通獎勵的概率為1-P*,平均每次抽獎返還稀有積分為F1×P*,返還普通積分為F2×(1-P*)。每張抽獎券的兌換價格為G1點稀有積分或G2點普通積分,集齊G1點稀有積分的平均抽獎次數為k1=G1/F1/P*,集齊G2點普通積分的平均抽獎次數為k2=G2/F2/(1-P*),兌換一張抽獎券的綜合平均抽獎次數為k=(k1×k2)/(k1+k2)。以抽獎券的兌換價格作為積分的價值標準,可得每點稀有積分的價值為C/G1,每點普通積分的價值為C/G2。
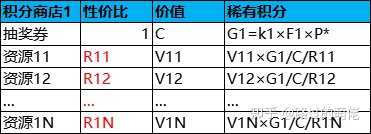
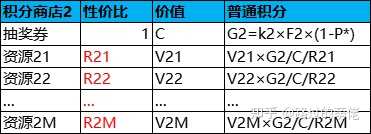
在此模型中,F1、F2、k1、k2、R1i、R2i為設定值,C、P*、V1i、V2i為已知值,而商品的兌換積分為匯出值。其中,F1、F2是可隨意取的,在盡量小的前提下保證其它推導結果均為整數即可;k1、k2取為10左右,且保證k也為10左右;R1i、R2i則根據具體專案需求自行設定。其中,積分商店1的商品多為稀有資源,積分商店2的商品多為普通資源。
5.3 實際套用
1)【明日方舟】的黃票和綠票
一般情況下,玩家得到5-6星幹員時返還黃票(稀有積分),得到1-4星幹員時返還綠票(普通積分),抽卡概率和返還數值如下:
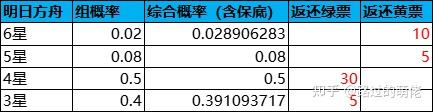
尋訪憑證(抽獎券)的兌換價格為258/38張黃票或450張綠票,即G1=258/38,G2=450。由此可逆向推匯出F1、F2、k1、k2等數值,如下所示:
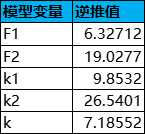
每次抽卡消耗為600合成玉,根據1源石=180合成玉=135理智(體力),600合成玉可換算為450理智,以理智作為標準價值單位,則C=450,每張黃票的價值為C/G1≈66.28,每張綠票的價值為C/G2≈1。
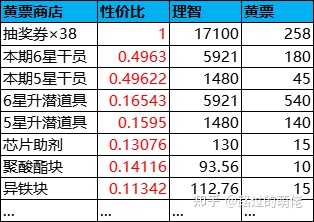
關於黃票商店,雖然明面上商品沒有劃分檔次,但可根據性價比的不同進行人為劃分。1檔商品為抽獎券,性價比為1,有限購上限,搬空需258張黃票,折算抽獎次數為258×k1/G1=376;2檔商品為本期幹員,性價比約為0.5,有限購上限,搬空需225張黃票,折算抽獎次數為225×k1/G1=328 ;3檔商品為升潛道具,性價比約為0.16,有限購上限,搬空需1360張黃票,折算抽獎次數為1360×k1/G1=1984;4檔商品為培養道具,性價比約為0.13,無限購上限。
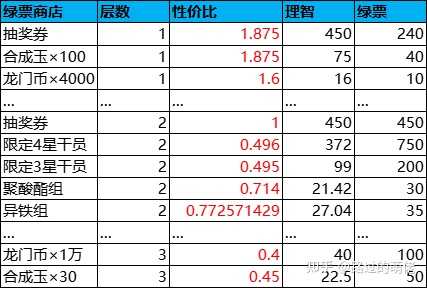
關於綠票商店,明面上商品直接劃分為三個檔位。1檔商品的性價比為1.5~2,有限購上限,搬空需1490張綠票,折算抽獎次數為1490×k2/G2=88;2檔商品的性價比為0.5~1,有限購上限,搬空需8800張綠票,折算抽獎次數為8800×k2/G2=522;3檔商品的性價比為0.4~0.45,無限購上限。
2)【原神】的星輝和星塵
一般情況下,玩家得到4-5星時返還星輝(稀有積分),得到3星時返還星塵(普通積分),抽卡概率和返還數值如下:
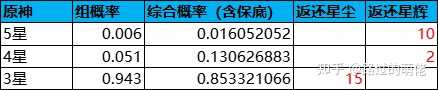
纏結之源(抽獎券)的兌換價格為5個星輝或75個星塵,即G1=5,G2=75。由此可逆向推匯出F1、F2、k1、k2等數值,如下所示:
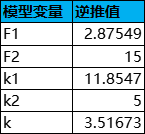
每次抽卡消耗為160原石,根據1原石=0.45樹脂(體力),160原石可換算為72樹脂,以樹脂作為標準價值單位,則C=72,每個星輝的價值為C/G1=14.4,每個星塵的價值為C/G2=0.96。
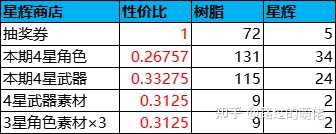
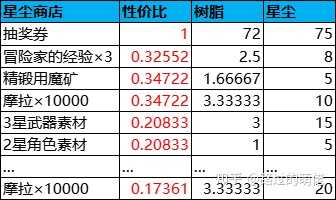
2023/3/26 20:27 更正:下面這段關於培養素材的價值樹脂的推導過程存在邏輯性錯誤(不要看,看了請忘掉),對資源價值分析有興趣的話可檢視本人的最新作品:【原神】的經濟數值模型分析。
關於培養素材的價值樹脂,首先看其主要獲取途徑(打怪掉落),然後以最高世界等級為前提,統計每天掉落數量。經過粗略統計,特定4星武器素材的每天掉落數量約為20,特定3星角色素材的每天掉落數量約為60。根據1樹脂=8分鐘,4星武器素材的價值樹脂為24×60/20/8=9,3星角色素材的價值樹脂為24×60/60/8=3。由於武器素材和角色素材的合成公式為3合1,於是3星武器素材的價值樹脂為9/3=1,2星角色素材的價值樹脂為3/3=1。關於星輝商店,1檔商品為抽獎券,性價比為1,無限購上限,每兌換1張抽獎券所需抽獎次數為k1≈12;2檔商品為本期角色和武器,性價比約為0.3,有限購上限,搬空需188個星輝,折算抽獎次數為188×k1/G1=446;3檔商品為武器素材和角色素材,性價比約為0.3,有限購上限,搬空需594個星輝,折算抽獎次數為594×k1/G1=1408。 對比【明日方舟】的黃票商店,最顯著的差異就是星輝商店的1檔商品(抽獎券)沒有限購上限,在一定程度上會影響重氪玩家的消費決策。
關於星塵商店,1檔商品為抽獎券,性價比為1,有限購上限,搬空需750個星塵,折算抽獎次數為750×k2/G2=50;2檔商品為經驗、魔礦和摩拉,性價比約為0.35,有限購上限,搬空需1300個星塵,折算抽獎次數為1300×k2/G2=87;3檔商品為武器素材和角色素材,性價比約為0.2,有限購上限,搬空需4740個星塵,折算抽獎次數為4740×k2/G2=316;4檔商品為無限摩拉,性價比約為0.17,無限購上限。
六、 動態獎池
6.1 基礎概念
在介紹動態獎池之前,首先要理解什麽是獎池,雖然前文也有稍微提及獎池的概念,不過並未給出具體定義,以下是本節關於獎池、靜態獎池、動態獎池的定義:
獎池:一組隨機獎品的有限集合,可記為P={(獎品i, 概率i)|i=1,2,...,N},概率總和為1。靜態獎池:獎品概率不隨抽獎次數的積累而變化的獎池。
動態獎池:獎品概率會隨抽獎次數的積累而變化的獎池。
根據上述定義,動態獎池的自變量為抽獎次數,因變量為獎品概率。獎品的變化可解釋為獎品概率的變化,比如獎品A變成獎品B可解釋為{(A, P*), (B, 0),...}→{(A, 0), (B, P*),...}。
前文提到的保底機制下的獎池其實就是一種動態獎池。由於獎品概率總和為1,保底大獎的概率提升必然伴隨其余獎品的概率下降。其概率變化規則采用「圓桌理論」,即優先剔除稀有度低的獎品概率。以【明日方舟】為例,尋訪卡池的6星保底為PRD保底模型PRD-GT(50, 99, 0.02, 0.02),5星、4星、3星的基礎概率分別為0.08、0.5、0.4,則關於抽獎次數的獎品概率分布如下:

6.2 幾種常見動態獎池
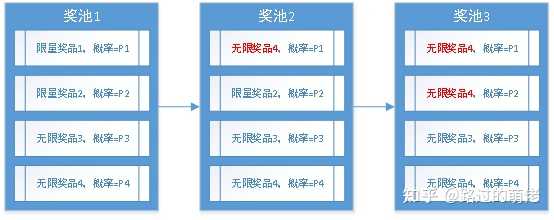
1)限量獎池
按照人群特征,限量可分為全服限量、公會限量、個人限量等;按照時間特征,限量可分為永久限量、活動限量、每周限量、每日限量等。限量獎品的中獎概率P依賴於其剩余庫存量L,當L>0時,P=P*;當L=0時,P=0。在程式上,這裏有兩種處理方法:其一是獎品跳轉,數值表現為跳轉獎品的中獎概率增加P*;其二是概率權重清零,數值表現為其余獎品的中獎概率增加P*的加權平均值。典型例子有:全服限量實物抽獎、個人限量道具抽獎、資源每日掉落上限等。
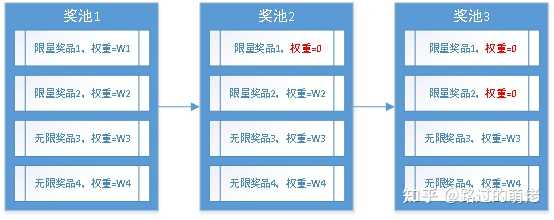
2)儲存獎池
現有一個貨幣儲存池,初始儲存值為S0,儲存下限為S_Min,儲存上限為S_Max。設當前貨幣儲存值為S,則活動開始時S=S0,全服玩家每次抽獎時S增加ΔS,玩家每次抽獎有機率P獲得數量為S×α的貨幣,同時S減少S×α,0<α<1。

對於該數值模型,每次抽獎獲得貨幣的期望值為S×α×P,顯然S越大,收益期望越高,這是不公平的。為了保證相對公平,一般會針對P關於S的變化進行分段取值,使得P和S呈反比例關系。
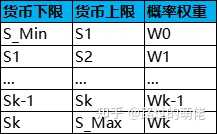
舉個例子,假設貨幣儲存池的貨幣類別與抽獎消耗的貨幣一致,S0=10000,S_Min=5000,S_Max=20000,每次抽獎消耗貨幣為50,ΔS=10,那麽S從S_Min到S_Max的最少累計抽獎次數為(S_Max-S_Min)/ΔS=1500。我們希望1500抽以內有99.99%的把握至少能抽到一次貨幣,即1-(1-P)^1500>0.9999,解得P≥0.0062。我們希望每次抽獎獲得貨幣的期望值約為抽獎消耗貨幣的20%,即S×α×P≈50×20%,令S=(S_Min+S_Max)/2=12500,P=0.0062,解得α≈0.13,為了使數值美觀,可取α=0.15。
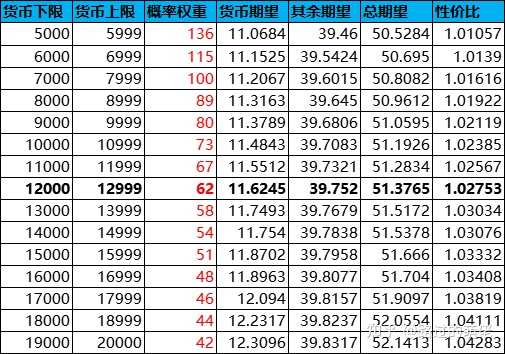
隨機獎品中,15%貨幣獎池的綜合概率為P=0.0062(概率權重=62),其余獎品的綜合概率為1-P=0.9938(概率權重=9938),綜合價值約為消耗貨幣的80%,即50×80%=40左右。對S的取值範圍[5000,20000]平均劃分為15個區間,P的分段取值如下,且貨幣期望=S×α×P≈(貨幣下限+貨幣上限)/2×0.15×概率權重/(概率權重+9938),其余期望=40×9938/(概率權重+9938),總期望=貨幣期望+其余期望,性價比=總期望/50。
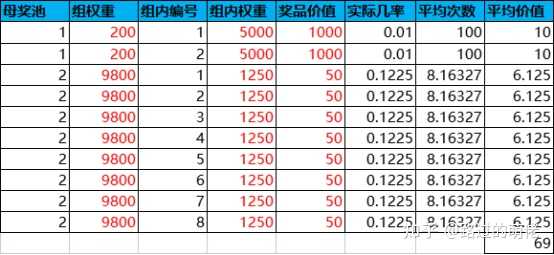
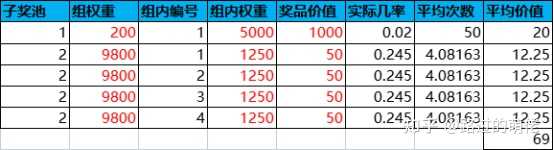
3)子母獎池
子母獎池一般為雙層抽獎模型,並且采用權重記法,子獎池為母獎池在一定規則下的非空真子集。初始獎池為隨機的某個子獎池,當個人抽獎次數積累到一定程度後,即可手動重設一次子獎池。當然,玩家也可選擇不重設,此時的獎池則退化為靜態獎池。
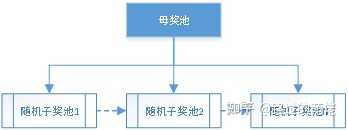
舉個例子,母獎池為2個大獎+8個小獎,子獎池為隨機1個大獎+隨機4個小獎,則子獎池的隨機組合數有C(2,1)×C(8,4)=140種。重設所需個人抽獎次數的設定可參考大獎的平均次數,比如取為50,即平均每抽中一次大獎即可獲得一次重設子獎池的機會。
4)平行獎池
設有N個獨立獎池,獎池i對應Wi張卡牌,卡牌總數為ΣWi,每一輪抽獎開始之前,對所有卡牌進行一次隨機洗牌,玩家可選擇翻開任意一張卡牌,若該卡牌對應獎池i,則從獎池i中隨機獲得一個獎品,直到翻完所有卡牌,進入下一輪抽獎。
若把每張卡牌視為一個個獨立獎品,則平行獎池相當於一種特殊的限量獎池。若每次翻開一張卡牌就放回去重新洗牌,則此時的獎池為雙層抽獎模型下的靜態獎池,Wi為獎勵組i對應的權重。 平行獎池的特征是隨機洗牌和不放回抽獎。這其實也是一種保底機制,保證了每輪抽獎必然能抽到一定次數的大獎。
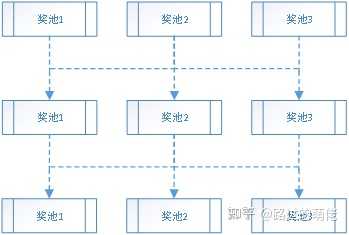
舉個例子,現有一個翻牌抽獎活動,共有10張卡牌,其中有1張金卡和9張銀卡,金卡對應稀有獎勵組,銀卡對應普通獎勵組。
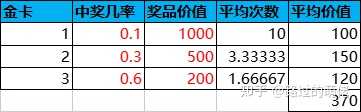
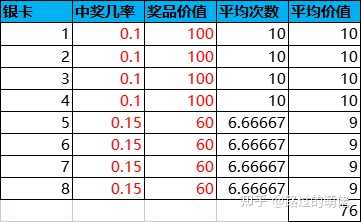
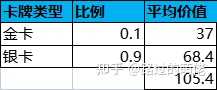
設每次抽獎消耗為100鉆石,玩家在實際抽獎過程中,一旦抽中金卡,那麽剩下的卡牌只有銀卡。此時,玩家若繼續選擇翻牌,則必然是虧損的,這不利於小R使用者的繼續消費。因此,翻牌抽獎一般會增加重設功能,即花費X鉆石重設所有卡牌。X的設定要參考抽中金卡的前提下繼續抽完剩余銀卡的總虧損。
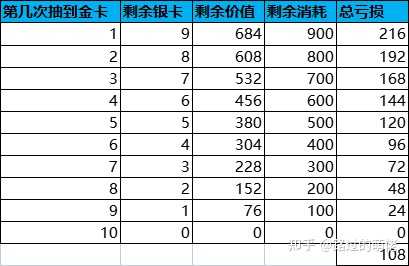
取X為100,介於96和120之間,即5次以內抽到金卡選擇重設是劃算的,6次以上抽到金卡選擇重設是虧損的。增加重設功能之後,抽中金卡的平均次數小於或等於10,平均次數的多少取決於玩家的重設方案。若一直不使用重設功能,則抽中金卡的平均次數為10;若每次抽中金卡後立即重設功能,則抽中金卡的平均次數達到最小值。
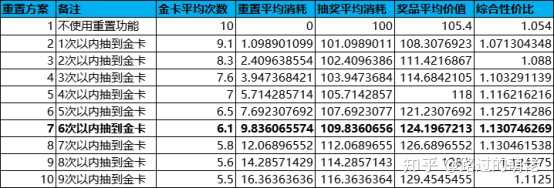
從綜合性價比來看,最佳重設方案是「6次以內抽到金卡選擇重設」。這裏說明一下,金卡平均次數利用古典概型來求解,每輪抽獎第幾次抽到金卡都是等概率的,總共有10種情況。因此,金卡平均次數=所有情況的翻牌總數/金卡總數。以「6次以內抽到金卡」為例,金卡平均次數=(1+2+3+4+5+6+10+10+10+10)/10=6.1。另外,重設平均消耗=X×P(6次以內抽到金卡)/每輪抽獎次數=100×0.6/6.1≈9.836。至於其它數據的計算就不多加說明了。
5)進階獎池
設有N個獎池,初始獎池為1階獎池,每次抽獎有Pi的概率從i階獎池進階為i+1階獎池,i=1, 2, ..., N。這裏的N+1階獎池表示1階獎池。一般而言,i階獎池的平均價值低於i+1階獎池的平均價值。於是,i階獎池的平均次數大於i+1階獎池的平均次數,即1/Pi>1>Pi+1,則Pi<Pi+1。也就是說,獎池的進階概率是遞增的。
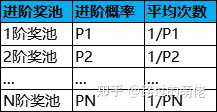

舉個例子,設有1-4階獎池,抽中稀有獎勵則進入下一階獎池,即Pi=P(抽中i階獎池的稀有獎勵)。每次抽獎消耗為100,數值設定如下表所示:
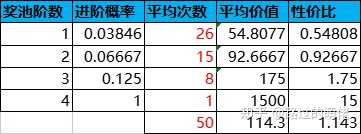
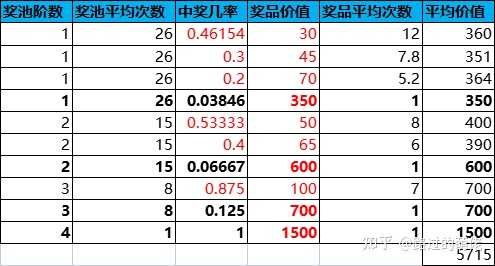
根據上述表格,抽獎性價比隨獎池階數的增加而遞增,低階獎池的性價比通常小於1,高階獎池的性價比大於1,最高階獎池的性價比是極高的。因此,進階獎池有一定的付費門檻,主要面向付費使用者。
七、 拓展與延伸
本質上,廣義的抽獎是一種「以小博大」的隨機性體驗。經過設計和糅合,這種體驗可以滲透到遊戲中的各個系統,比如戰鬥、養成、玩法等。在遊戲中,隨機性雖然提供了豐富的多變性,但也難免伴隨著一定程度的不可控性。因此,我們在設計遊戲的隨機性體驗時,也要考慮是否對隨機性加入人為幹預,避免隨機性失控而對遊戲的本質體驗造成嚴重的負面影響。
7.1 隨機性指標
1)隨機振幅
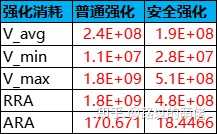
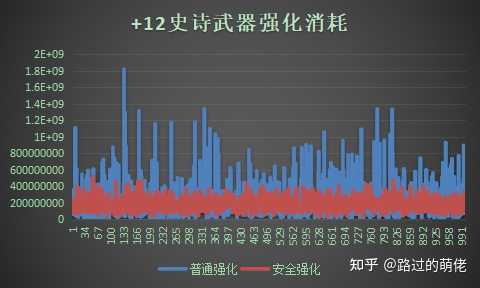
隨機振幅(RA)是指一個隨機過程的最大效益(V_max)和最小效益(V_min)的差距,可分為絕對隨機振幅和相對隨機振幅。比如一次抽獎的最好獎品價值為1000,最差獎品價值為50,每次抽獎消耗為100,則V_max=1000-100=900,V_min=50-100=-50,ARA=900-(-50)=950,RRA=+∞。
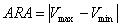
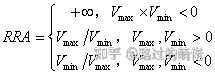
2)隨機頻次
隨機頻次是指一個隨機過程在某個時間段內發生的總次數。比如一次十連抽相當於10次單抽,隨機頻次為10。
假設某個隨機過程A1重復執行n次形成一個復合隨機過程An,記An的隨機振幅為RAn,則有:
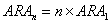
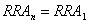
3)概率分布
一個復合隨機過程An的概率分布為(P1, P2, ... ,Pn),若P1=P2=...=Pn,則An為靜態概率分布,否則為動態概率分布。比如直接/PRD保底機制下的n次抽獎過程就是動態概率分布。
7.2 隨機性控制
適度的隨機效能讓遊戲體驗變得豐富有趣,但失控的隨機性也會讓遊戲體驗變得糟糕透頂。隨機性失控的根本原因是隨機振幅過大而造成遊戲體驗變質。
1)控制隨機振幅
2)增加隨機頻次
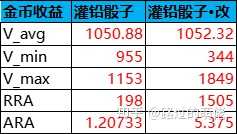
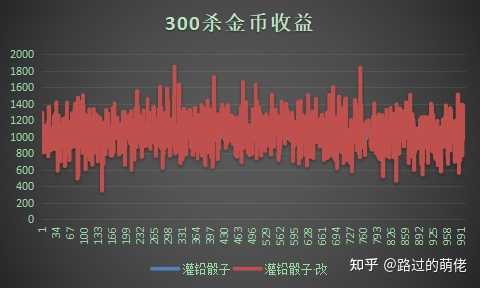
3)動態概率分布
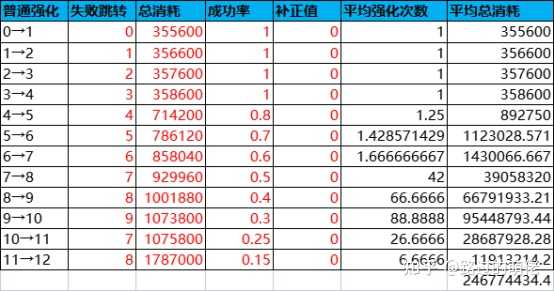
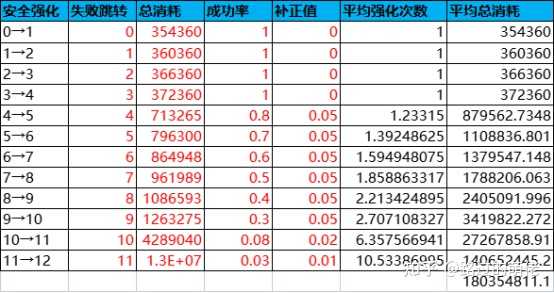
八、VBA程式碼附錄
Sub 模擬抽獎()
Dim N As Integer
N = 200
Call 無保底(0.02, N)
Call 直接保底(0, 100, 0.016, N)
Call PRD保底(57, 156, 0.01, 0.01, N)
End Sub
Sub 無保底(p As Double, N As Integer)
Dim i As Integer
Dim k As Integer
k = 0
For i = 1 To N
再抽一次:
k = k + 1
If Rnd < p Then
Sheet1.Range("A" & i + 1) = k
k = 0
Else
GoTo 再抽一次
End If
Next
End Sub
Sub 直接保底(A As Integer, B As Integer, p As Double, N As Integer)
Dim i As Integer
Dim T As Integer
Dim k As Integer
T = 1
k = 0
For i = 1 To N
再抽一次:
k = k + 1
If T <= A Then
T = T + 1
GoTo 再抽一次
ElseIf T < B Then
If Rnd < p Then
Sheet1.Range("B" & i + 1) = k
T = 1
k = 0
Else
T = T + 1
GoTo 再抽一次
End If
Else
Sheet1.Range("B" & i + 1) = k
T = 1
k = 0
End If
Next
End Sub
Sub PRD保底(A As Integer, B As Integer, p As Double, pp As Double, N As Integer)
Dim i As Integer
Dim T As Integer
Dim k As Integer
T = 1
k = 0
For i = 1 To N
再抽一次:
k = k + 1
If T <= A Then
If Rnd < p Then
Sheet1.Range("C" & i + 1) = k
T = 1
k = 0
Else
T = T + 1
GoTo 再抽一次
End If
ElseIf T < B Then
If Rnd < p + (T - A) * pp Then
Sheet1.Range("C" & i + 1) = k
T = 1
k = 0
Else
T = T + 1
GoTo 再抽一次
End If
Else
Sheet1.Range("C" & i + 1) = k
T = 1
k = 0
End If
Next
End Sub











