過去十年中航空航天領域最重要的科學進展是SpaceX的工程師在2012年發表的論文"Lossless Convexification of Nonconvex Control Bound and Pointing Constraints of the Soft Landing Optimal Control Problem"(對最優軟著陸問題中非凸的控制約束和朝向約束進行無失真凸化),正是這篇論文中討論的技術點讓可回收火箭成為可能。從這篇論文我們可以思考並理解到很多重要的科研、人才培養的問題。
最優軟著陸問題介紹
「過去十年中航空航天領域最重要的科學進展」這個評價是我的博士導師Zachary Manchester做出的。由於Zac的博士導師Mason Peck曾擔任過NASA的首席技術專家,且Zac自己在NASA Ames Center工作過一段時間,所以這個評價非常令人信服。我們簡單科普一下這篇論文的內容,若要詳細理解論文的基本技術細節需要首先通讀【Numerical Optimization】和【Convex Optimization】兩本教科書,如果要進一步看懂論文所有的證明,還需要深入學習最優控制理論。
論文探討的是「最優軟著陸問題」(Soft Landing Optimal Control Problem)。在人類歷史上的地外行星探測任務中,探測器著陸不是一件非常困難的事情,但是對於可回收火箭來說,軟著陸的難度極大。以往人類只在月球和火星進行過軟著陸,最常用的方法是在探測器近地面的時候點燃反推發動機減速,比方說嫦娥五號登月就用了這種方式。

由於月球重力低,登月艙相對較輕,反推發動機不需要長時間執行,所以很容易做出推力巨大的發動機來實作這件事。一般反推發動機執行時可產生幾倍於火箭重力的推力(推重比),這讓登陸器能夠在落地前大力出奇跡地把速度降低。
但是可回收火箭回地球軟著陸的時候,反推的推力是有限的。一方面地球重力較大,另一方面火箭本身除了主發動機以外不可能再安裝額外的反推發動機,因此降落期間的推重比一般在1.2到1.5之間,火箭不能只在降落前十秒鐘才開始進行反推,而是要從高空開始就規劃一條運動軌跡,持續調整控制發動機的輸出,為此,火箭控制器需要在全降落過程中每時每刻即時解算兩個帶約束的非線性最佳化問題。

本論文中不僅構造了火箭軟著陸的最佳化問題,並且提出了有嚴密證明支撐的重構方法,讓軟著陸最佳化問題能夠在實際火箭上快速求解。下一節我們簡單介紹一下論文中對於軟著陸最佳化問題的求解過程,如果不想看太多數學運算式的話可以略過這一節。
重構軟著陸的非凸最佳化問題
軟著陸中有兩個需要被求解的最佳化問題是這樣的:

這兩個問題形式非常類似,在實際中需要一起被求解,問題2的解與問題1的解有關,問題2最後解出的是火箭在全過程中每個時刻應該施加的推力值,如果問題解算得足夠快,它就可以被用於一個模型預測控制器中用來生成給發動機的推力輸出值。其中第一個問題比較重要,它描述的是:「給定火箭初始的位置( r(0)=r_0 ,速度( \dot{r}(0)=\dot{r}_0 )和燃料質素( m(0)=m_0 ),我們希望求解火箭從開始到時間 t_f 期間的推力函數 T_c(t) ,使得火箭在時間 t_f 後降落到海平面高度( e_1^Tr(t_f)=0 ),降落時速度恰好為0( \dot{r}(t_f)=0 ),且剩余燃料量大於一定值( m_f )。在此期間,火箭的位置、姿態和燃料的消耗量必須滿足運動狀態方程式(4),位置和姿態必須處於一定的空間內(5)。最重要的是,火箭輸出的推力 T_c(t) 必須滿足兩個約束條件(6)」。雖然看起來復雜,但是這可以化成標準的有約束非線性最佳化形式,並且使用成熟的非線性最佳化工具比如IPOPT求解。讀者可以先不用關心每個公式具體的意義,可以只對比上述問題和下面這個構造的相似之處。
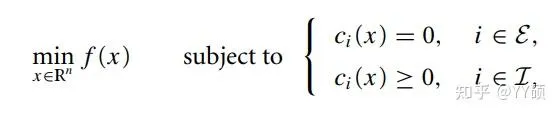
這個問題雖然可以被最佳化工具求解,但是一直以來被認為沒有什麽用——因為這個問題是非凸最佳化問題,求解需要大量的時間,下面我們簡單說說凸最佳化和非凸最佳化。
世界上有兩類有約束的最佳化問題,一類是凸的,另一類是非凸的。兩者的區別是最佳化問題的變量的可行域是否是凸集。如下圖(A)組中兩個形狀的可行域是凸集,(B)組中兩個則是非凸集,凸集的定義是「集合中任兩點間的連線上的點仍在集合中的集合」。感性地理解凸與非凸對於最佳化的影響是,我們現在所掌握的數學工具只允許我們從集合中的某點開始在可行域中透過某些方式連續移動,期望能夠尋找到讓代價函數最小的一個點。在凸集中,最佳化過程中點的移動幾乎都可以直線移動不受什麽限制,而在非凸集中,比如B組中的集合,想要從P1點移動到P2點而不離開集合內部需要走個拐彎,這樣「走」並不好用數學語言去描述。因此在非凸集合上的最佳化大大難於在凸集上的最佳化。
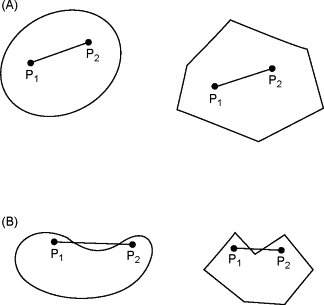
凸最佳化和非凸最佳化的關系很類似電腦科學裏面的P與NP問題,P問題有高效求解的演算法,可以在短時間內求解,而NP問題沒有,通常要計算非常久的時間;NP問題透過巧妙的重新構造有時可以變成P問題,但是沒有通用的重構方法。而且,就像我們不知道P是否等於NP一樣,我們不知道是不是所有的非凸問題都能夠重新構造成凸問題。
軟著陸問題是非凸最佳化的原因是,火箭推力 T_c 的約束條件 0<\rho_1\leq\|T_c(t)\|\leq\rho_2 以及 \hat{n}^TT_c(t)\geq\|T_c(t)\|cos\theta 使得推力的可行域是一個非凸的集合,也就是下圖中深藍色的區域:
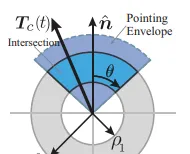
可行域這個環狀的結構部份(圖中灰色的區域)是由於火箭推力有最大值也有最小值導致的。其他答主有提到Space X的梅林發動機是世界上超一流的高推重比發動機,但是梅林發動機整合到火箭上之後依然只有最多不超過1.5的推重比(別忘了火箭還需要有可伸縮的起落架結構)。因此火箭整體的推力有很低的上限,另外火箭在空中也沒法把發動機停下來,所以有推力的下限。推力的上下限帶來了非凸的可行域集合。
對於火箭控制,控制問題是凸還是非凸的區別會導致控制器能不能高頻對火箭施加控制。SpaceX並沒有公開可回收火箭的工程技術細節,根據其他火箭系統推斷,我覺得合理的控制頻率應該在10Hz以上,因此火箭的飛控電腦必須能夠在100ms內解出上述最佳化問題,然而上述這個非凸最佳化求解一次需要的時間以秒為單位(在效能較好的桌面電腦上一般需要求解5-10秒鐘),遠遠不足以用來生成高頻控制量。
這篇論文中的解法是把推力的約束條件重構成如下形式:
\|T_c(t)\|\leq\Gamma(t) \\ 0 < \rho_1\leq\Gamma(t) \leq \rho_2 \\ \hat{n}^TT_c(t) \geq \cos\theta \ \Gamma(t)
其中 \Gamma(t) 是額外引入的一個待最佳化變量,這是最佳化中常用的方式——透過增加最佳化變量來重構某些約束。在這個問題裏 \Gamma(t) 代表推力的上限值。這樣重構之後,推力的可行域變成了如下形式的凸集(假設我們研究二維平面內的控制問題,推力只有2維)
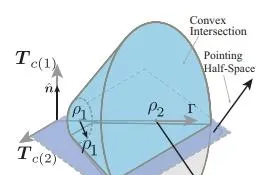
這是一個被切了兩刀的圓錐體,滿足我們之前所說的凸集的定義。進行重構後,需要被求解的問題1就變成了如下的問題3
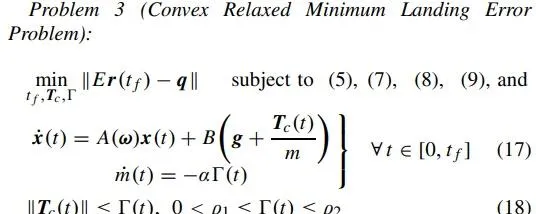
而問題2則可以被重構成下面的問題4,這是一個凸最佳化問題

這個變形看似簡單,但是蘊涵著極豐富的數學原理。為什麽這樣的重構是等價的呢?換句話說,如何確保重構後的凸最佳化問題的解也是原來非凸最佳化問題的解呢?要知道火箭控制中安全至關重要,如果沒有十足的理論證明,這樣的重構是不可靠的。於是論文中最精華的部份來了——作者們透過極嚴密的數學推導,證明問題4和問題3的解一定和問題2同問題1等價,證明中需要用到最優控制中的哈密爾頓函數以及龐泰利亞金最大化原理。但是慚愧地說,雖然我自認認真學習過最優控制理論,也在數值最佳化領域實踐了兩年,能夠用各種仿真工具按照論文做出可回收火箭的降落控制器,但是這個證明我暫時還沒有完全看懂。如果有讀者看懂且能夠把詳細的步驟寫出來,希望有機會可以交流交流。
軟著陸最佳化問題快速求解的意義
上一節中我們簡單瀏覽了論文中將軟著陸問題由非凸最佳化變換成凸最佳化的過程。在論文的結束語中作者們只是含蓄地講到"This convexification enables the planetary soft landing problem to be solved optimally by using convex optimization, and is hence amenable to onboard implementation with a priori bounds on the computational complexity and realtime execution time."(這個變換讓行星軟著陸問題可以作為凸最佳化問題被求解,因此能夠在有計算復雜度限制和即時計算限制的機載電腦上被執行)。通常來說,一個非線性最佳化問題由非凸最佳化重構成凸最佳化之後計算速度可以指數級提升,因此火箭的主控電腦能夠以10Hz或者更高的頻率計算軟著陸過程中火箭需要的推力,從而實作對火箭的模型預測控制。在論文發表後不久的2013年,Space X開始測試名為Grasshopper的火箭,將論文中討論的最佳化演算法實作在了真火箭上。
隨後的故事世人皆知。2013年我剛加入大疆,當時只知道Space X測試Grasshopper時用了大疆的S600六軸飛行器做拍攝,卻不知其背後激動人心的數學和最佳化技術的進展。所以回頭再看的話,說這篇論文是「過去十年中航空航天領域最重要的科學進展」並不誇張。我輩生也晚,人類歷史上偉大的工程學進展大多只是書中的記載,而如今這「讓人類成為星際文明生物」的科技發展,不僅有詳實的影像,還有其背後的數學和工程學基礎知識可以閱讀,實在是一種幸運。
另外這項科研也給有誌攀登科學和工程學高峰的研究人員特別是博士生指出了如何進行有價值研究工作的思路:針對一個已經或者接近投入大規模使用的控制系統(火箭),提出一個方法讓該系統能夠具有新的功能或者顯著提高已有的功能(顯著提高軟著陸的效率),有嚴密的數學推導證明(由最優控制理論證明凸變換的有效性),能夠在實際系統上驗證(Space X Grasshopper火箭)。我自己就在自己的研究領域試圖尋找這樣的工作。
從論文說開去
2013年之後,隨著Space X可回收火箭的成功,航空航天和機器人領域的研究人員開始重新看待基於最佳化的控制演算法和軌跡生成演算法。幾年後波士頓動力也開始展示Atlas機器人使用基於最佳化的軌跡規劃演算法進行的跳舞、跑酷等動作。我的導師Zachary Manchester在2012-2013年間在NASA Ames Research Center工作,經歷了Space X這一系列開天辟地的壯舉,也在NASA內耳濡目染了其中的原理(讀者可能註意到Space X和NASA進行了大量的合作,特別是早期的軟著陸問題只有NASA在研究,SpaceX獲得成功後,NASA體制內的工程師都非常羨慕嫉妒恨),於是他在博士畢業後加入了哈佛教授Scott Kuindersma的實驗室做博士後,研究復雜控制系統的非線性最佳化問題。Scott Kuindersma後來加入了波士頓動力公司,繼續在Atlas機器人上研發非線性最佳化控制器。因此Space X可回收火箭極大促進了各種相關領域的發展。直到今天,非線性最佳化和模型預測控制成為了當代最優秀的一些機器人和復雜控制系統的主流技術(並不是強化學習),其中依然有豐富的數學和工程學問題可以探索。我認真學習了幾年,最近也稍稍小有所得。
2022年,紀錄片Return To Space(【重返太空】)上映,這個詳細記錄Space X從誕生到成功實作載人航天飛行全過程的紀錄片非常有意思。我們談論的這篇論文的通訊作者Lars Blackmore在裏面簡短出鏡,用大眾聽得懂的語言介紹了一下可回收火箭的原理,結果聽起來毫不激動人心,畢竟這項工作的精華是很少有人了解的凸最佳化。Lars Blackmore的經歷很值得說道說道,他是英國人,在劍橋大學讀完本科和研究生後,到美國麻省理工學院讀完了博士學位,2007年畢業後在NASA噴射推進實驗室工作到2011年,主要參與火星軟著陸控制,然後加入Space X研究可回收火箭降落至今。可以說是英美兩國最好的教育資源一起培養出來的人才。
除了Lars Blackmore以外,Space X在紀錄片中出鏡的工程師幾乎都是「外國人」:Hans Koenigsmann出鏡最多,德國人,本科和博士學位均在德國獲得。根據美國網友不知何處聽來的小道訊息我們現在大概知道在Hans Koenigsmann的帶領下Space X設計了一套使用3台消費級電腦x86處理器同時執行6個相同的飛控程式的冗余飛控方案——SpaceX使用消費級電腦硬件革命性地改變航天電腦的設計思路是另一個激動人心的話題,我們暫且先按下不表。另外一個出鏡的工程師Balachandar Ramamurthy,飛行安全技術總監,則是印度人,在印度獲得本科學位。再有一位負責發射的副總裁Kiko Dontchev,看背景是實打實的美國人,本科和研究生都在密西根大學獲得,但是他的姓Dontchev是罕見的保加利亞後裔才有的姓氏。
此外,如果有讀者註意到——可回收火箭論文的一作Behçet Açıkmese是土耳其人,在土耳其獲得本科學位後,繼續在美國獲得博士學位,透過最優控制理論證明凸化的準確性的數學證明八成是他做出的,這種水平的證明全世界可能只有不到十個人能做出來。最後,眾所周知——Space X的創始人Elon Musk是南非人。
所以Space X的成果離不開各個國家匯集到美國的人才的共同努力。太空探索作為人類套用物理學和工程學的最前沿,一定需要人類各個民族共同的參與。因為一些政治悲劇,美國的NASA不能和中國航天機構合作,但是不管美國是搬起石頭砸自己的腳也好,霸權主義也好,撇開政治不談,這個國家對於太空探索這件事情構建了一個從產業鏈到科研院所組織再到能夠吸聚全人類人才的移民體系的全方面社會架構。領導太空探索這件事已經成為了美國構建民族意識的最好媒介之一。因此美國即使排斥和中國的合作,依然能夠不斷透過從其他國家移民來補全航天的人才梯隊。當有誌於成為太空探索領導者的中國在當代挑戰美國的地位時,人們常常忽略吸聚人才的重要性,這是中國需要學習和提高的地方。
不過我們更希望在未來,任何一個優秀的工程師都能自由地在地球上任何一個航天機構從事科研開發,所有的航天機構都能分工合作,地球上所有的人們都能摒棄國家和種族的紛爭,真正地攜手走向星際文明時代。











