这个问题很有意思,这种「先微后积」的方法民间被称为Feynman's Trick
我第一次见到这种方法是高二参加某划水竞赛的时候
当时有一道题遇到了这么一个积分(我另外一个回答里也有提到)
\int_0^\pi \ln(a^2 -2a\cos x+1)\,\mathrm dx
其中常数 a\ge 1 (见图片第10题位置)
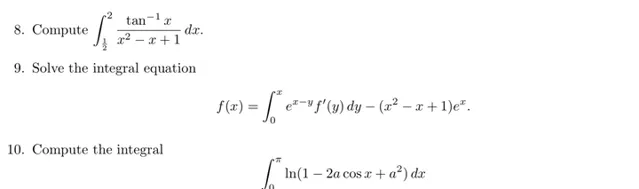
这道题原题来自 Putnam and Beyond 的 Problem 471
这个积分其实设计的非常巧妙,答案里有五种方法:用Riemann sum的解法,用Chebyshev polynomial的解法,转换为物理问题的解法,用留数定理的解法,还有一种就是Feynman's Trick,也是相对比较容易理解的一种做法
Feynman's Trick的主要步骤是这样的
对于带参数的定积分 I(t)=\int_{a(t)}^{b(t)}f(x, t)\,\mathrm dx
其中 -\infty<a(x), b(x)<\infty 且 a, b,\frac{\mathrm da}{\mathrm dt}, \frac{\mathrm db}{\mathrm dt}, \frac{\partial f}{\partial t} 连续
1.首先,我们对 t 微分,由 Leibniz integral rule (后面会讨论其证明)得到
\frac{\mathrm d}{\mathrm dt}\int_{a(t)}^{b(t)}f(x, t)\,\mathrm dx=\int_{a(t)}^{b(t)} \frac{\partial f}{\partial t}\, \mathrm dx + f(b(t), t)\frac{\mathrm db}{\mathrm dt}-f(a(t), t)\frac{\mathrm da}{\mathrm dt}
特别的,如果上下限是常数 a, b
\frac{\mathrm d}{\mathrm dt}\int_{a}^{b}f(x, t)\,\mathrm dx=\int_{a}^{b} \frac{\partial f}{\partial t}\, \mathrm dx
2.然后,求出 I(t) ,往往求出来会带着一个积分常数
3.最后,通过一个特殊值 I(t_0)=c 解出积分常数
举个例子,已知常数 a, b \in \mathbb{R} ,求定积分
I(a, b)=\int_0^\infty \frac{\tan^{-1}ax-\tan^{-1}bx}{x}\, \mathrm dx
首先,我们对 a 微分(可证一致收敛)
\frac{\partial I}{\partial a}=\int_0^\infty \frac{1}{x}\frac{\partial}{\partial a}\tan^{-1}ax\, \mathrm dx=\int_0^\infty\frac{\mathrm dx}{1+a^2x^2}=\frac{\pi}{2a}
所以我们能知道 I(a, b)=\frac{\pi \ln a}{2}+f(b) ,其中 f 是我们未知的一个函数
因为 I(a, a)=0 ,所以 I(a, b)=\frac{\pi}{2}\ln\left( \frac{a}{b}\right)
其实这个积分是一个Frullani积分
如果一个函数 f:\mathbb{R}\rightarrow \mathbb{R} 满足在 x\ge 0 上有定义且 f(\infty) 存在
那么我们称
\int_0^\infty \frac{f(ax)-f(bx)}{x}\, \mathrm dx
为一个Frullani积分
如果 \frac{\mathrm d f}{\mathrm dx} 连续,我们可以通过Feynman's Trick证明
\int_0^\infty \frac{f(ax)-f(bx)}{x}\, \mathrm dx=(f(\infty)-f(0))\ln\left(\frac{a}{b}\right)
看到这里有的读者可能会问「这个 Leibniz integral rule 是怎么证明的呢?」
\frac{\mathrm d}{\mathrm dt}\int_{a(t)}^{b(t)}f(x, t)\,\mathrm dx=\int_{a(t)}^{b(t)} \frac{\partial f}{\partial t}\, \mathrm dx + f(b(t), t)\frac{\mathrm db}{\mathrm dt}-f(a(t), t)\frac{\mathrm da}{\mathrm dt}
在Inside Interesting Integral一书中,Paul J. Nahin给出了一个证明


另外一个Feynman's Trick的经典应用是Probability integral的证明
\int_{-\infty}^{\infty}e^{-\frac{x^2}{2}}\mathrm dx=\sqrt{2\pi}
很多概率分布的概率密度函数的积分中都会出现这个东西,一种方法是把它平方,化成二重积分,转为极坐标求解,但用Feynman's Trick也同样可以求得。
我们首先设 I(t)=\left(\int_{0}^{t}e^{-\frac{x^2}{2}}\mathrm dx\right)^2 然后对 t 微分
\frac{\mathrm dI}{\mathrm dt}=2\left(\int_{0}^{t}e^{-\frac{x^2}{2}}\mathrm dx\right)e^{-\frac{t^2}{2}}=2\int_0^t e^{-\frac{x^2+t^2}{2}}\mathrm dx
进行 y=\frac{x}{t} 换元,我们能得到
\int_0^t e^{-\frac{x^2+t^2}{2}}\mathrm dx=\int_0^1 e^{-\frac{(1+y^2)t^2}{2}}t\,\mathrm dy
因为 e^{-\frac{(1+y^2)t^2}{2}}t=\frac{\partial}{\partial t}\left(\frac{-e^{-\frac{(1+y^2)t^2}{2}}}{1+y^2}\right) 所以我们有
\frac{\mathrm dI}{\mathrm dt}=2\int_0^1 e^{-\frac{(1+y^2)t^2}{2}}t\,\mathrm dy=-2\frac{\mathrm d}{\mathrm dt}\int_0^1\frac{e^{-\frac{(1+y^2)t^2}{2}}}{1+y^2}\,\mathrm dy
所以
I(t)=-2\int_0^1\frac{e^{-\frac{(1+y^2)t^2}{2}}}{1+y^2}\,\mathrm dy+\mathrm{constant}
我们让 t=0 ,因为
I(0)=\left(\int_{0}^{0}e^{-\frac{x^2}{2}}\mathrm dx\right)^2=0
我们又知道
I(0)=-2\int_0^1\frac{1}{1+y^2}\,\mathrm dy+\mathrm{constant}=-\frac{\pi}{2}+\mathrm{constant}
所以积分常数是 \frac{\pi}{2}
I(t)=\frac{\pi}{2}-2\int_0^1\frac{e^{-\frac{(1+y^2)t^2}{2}}}{1+y^2}\,\mathrm dy
最终能得到
\int_{-\infty}^\infty e^{-\frac{x^2}{2}}\mathrm dx=2\sqrt{I(\infty)}=2\sqrt{\frac{\pi}{2}}=\sqrt{2\pi}
一开始的那个积分的答案是 \int_0^\pi \ln(a^2 -2a\cos x+1)\,\mathrm dx=2\pi \ln a
以下是证明
首先我们设一个函数 I:\mathbb{R}\rightarrow \mathbb{R}
I(a)=\int_0^\pi \ln(a^2 -2a\cos x+1)\,\mathrm dx
接下来我们对 a 求微分,并把积分和微分符号交换
\frac{\mathrm d I}{\mathrm da}=\int_0^\pi \frac{\partial}{\partial a}\ln(a^2 -2a\cos x+1)\, \mathrm dx=\int_0^\pi \frac{2a-2\cos x}{a^2-2a\cos x + 1}\, \mathrm dx
接着我们通过一个万能的三角函数换元 t=\tan\frac{x}{2} ,然后整理一下
\frac{\mathrm d I}{\mathrm da}=\int_0^\infty\frac{2a-2\frac{1-t^2}{1+t^2}}{a^2-2a\frac{1-t^2}{1+t^2}+1}\cdot\frac{2}{1+t^2}\,\mathrm dt=4\int_0^\infty \frac{(a+1)t^2+(a-1)}{(a+1)^2t^2+(a-1)^2}\cdot\frac{\mathrm dt}{1+t^2}
这样我们就可以把这个积分拆成两个积分的和
\begin{align}\int_0^\infty \frac{(a+1)t^2+(a-1)}{(a+1)^2t^2+(a-1)^2}\cdot\frac{\mathrm dt}{1+t^2}&=\frac{2}{a}\int_0^\infty \frac{a^2-1}{(a+1)^2t^2+(a-1)^2}\,\mathrm dt \\&+\frac{2}{a}\int_0^\infty \frac{\mathrm dt}{1+t^2}\end{align}
做换元 t\rightarrow \frac{a+1}{a-1}t 我们就能发现第一个积分和第二个相等
\int_0^\infty \frac{a^2-1}{(a+1)^2t^2+(a-1)^2}\,\mathrm dt =\int_0^\infty \frac{\frac{a+1}{a-1}}{1+\left(\frac{a+1}{a-1}\right)^2t^2}\,\mathrm dt=\int_0^\infty \frac{\mathrm dt}{1+t^2}
所以,代回上面的式子,我们就能得到
\frac{\mathrm d I}{\mathrm da}=\frac{4}{a}\int_0^\infty \frac{\mathrm dt}{1+t^2}=\frac{4}{a}\bigg[\tan^{-1} t\bigg]_0^\infty=\frac{2\pi}{a}
也就是说 I(a)=2\pi \ln a + \mathrm{constant}
接下来我们只需求出一个特殊值 I(1)
I(1)=\int_0^\pi \ln(2-2\cos x)\, \mathrm dx=\pi \ln 2 +\int_0^\pi\ln\sin x \, \mathrm dx
设后面的这个积分 J=\int_0^\pi \ln\sin x \,\mathrm dx 那么
\begin{aligned}J&=\int_0^\frac{\pi}{2} \ln \sin x\, \mathrm dx+\int_\frac{\pi}{2}^\pi \ln \sin x\,\mathrm dx=\int_0^\frac{\pi}{2} \ln \sin x\,\mathrm dx+\int_0^\frac{\pi}{2} \ln \cos x\,\mathrm dx\\&=\int_0^\frac{\pi}{2}(\ln\sin 2x-\ln2)\,\mathrm dx=\frac{1}{2}\int_0^\pi \ln \sin x\,\mathrm dx-\frac{\pi\ln2}{2}\end{aligned}
所以 J=\frac{J}{2}-\frac{\pi\ln2}{2} 我们就得到 \int_0^\pi \ln\sin x \,\mathrm dx=-\pi \ln 2
所以 I(1)=0 ,所以 I(a)=2\pi \ln a
从Feynman's Trick可以延伸出来很多骚操作,比如把待求积分变成一个二阶线性齐次微分方程进行求解,甚至把Feynman's Trick倒过来用(对参数积分)等等,以后有时间再补充。
最后留一道积分给读者练手
\int_0^\infty e^{\cos x}\sin\left(\sin x\right)\,\frac{\mathrm dx}{x}
Reference
1.Paul J. Nahin, 2014, Inside Interesting Integrals , ISBN 978-1-4939-1276-6
2.Razvan Gelca and Titu Andreescu, 2007, Putnam and Beyond , ISBN-13: 978-0-387-25765-5











