首先,关于时间箭头,涉及到科学和哲学的广泛讨论,包括诸如 因果箭头、心理学箭头、热力学箭头、电动力学箭头、宇宙学箭头、量子力学箭头 等等。本文尽量弱化哲学讨论,尽可能地聚焦在科学角度。主要谈论一下热力学和量子力学箭头。(已有答主从时空结构的角度谈论过这个问题了,这里我不再狗尾续貂)
0,在谈论之前我先澄清一件事。
当我们说「时间箭头是单向的」或者「流动是单向的」,我们说的是什么东西?
从表面的语义上来看,我们假定存在着一种东西,叫做「时间」。这种东西是在流动的 - 它的流动方向不受任何事物的影响,总是「朝前」的。
但是,从物理学的角度,更加自然的做法不是去讨论「时间本身」的「流动」,而是把时间作为一个事件有序排列的维度。所谓的「时间箭头」,不是时间本身是不是有一个箭头,而是讨论 在时间维度上,物理现象的不对称性 。也就是说,在时间序列中,它的两端有着显著差异,于是我们就有了「历史」和「未来」的区别。是事件序列的不对称性赋予了「时间」一个箭头。
我可以姑且把前者叫做「时间流动」图景,后者叫做「时间序列」图景。
至于为何我们不采取第一种 把时间看做是一种流动的实体 的看法,我们后面再说。
另外,关于时间箭头的科普可谓是汗牛充栋。但是真正说得特别清楚明白的,却不多见,往往失于偏颇,或者根本就不能解决问题。这里我向大家推荐一本科普著作:
Sean Caroll写的 From Eternity to Here: The Quest for the Ultimate Theory of Time . [1]
语言简单,并且论述相当清楚。亚马逊的audible还有他自己朗读的有声书,不得不说,他的声音也挺好听,并且读得十分清晰,听力不好的人都可以听明白,开车的时候听一听,非常有舒缓心情之功效。
1,首先说一下热力学箭头。
所谓热力学箭头,指的就是热力学第二定律的结论:孤立系统的熵总是增加。如果我们把整个宇宙看做是一个孤立系统,那么宇宙的熵就是不断增加的。那么,在整个宇宙的历史线上,就必然 两端不对称 :一端低熵,我们称之为「历史」,另一端高熵,我们称之为「未来」。于是,熵就成了一种时间箭头。
我的历史回答中,曾经详细谈论过一个问题,就是为何微观定律时间可逆,热力学上却总是熵增?诸如这两个答案:
这里的核心问题就是,从底层的动力学方程中,我们看不到时间的两个方向上有所区别(也就是说,我们把方程做一个时间反演操作,所有的物理学定律仍然成立)。无论是经典力学还是量子力学,都没有对「时间方向」有所限制。但是为何建立在这些方程基础之上的熵增定律却明确地规定了世界必须从低熵向高熵演化?
统计力学对此的回答,现在尚有争论。但是现有的比较公认的有两件事,简言之:
- 相空间的结构是不对称的
- 初始条件问题
用「人话」来讲,就是
- 高熵是极大可能出现的状态,低熵是基本上不可能出现的状态
- 我们现在的宇宙状态就是极不可能出现的低熵态
下面我一一道来。
1.1,相空间的不对称性
在讲这个之前,我要说明一下,下面这一小节基本上都是从经典物理图景出发来阐述的。这是因为,从经典向量子的推广,并没有什么原则上的限制。并且关于量子的讨论我们可以展开一点点,放在后面。
好了,现在我们来说一下,什么是相空间呢?
理论上,我们可以把构成宇宙的所有粒子的状态(经典物理上,就是每一个粒子的动量和位置,量子物理上,就是态矢量)描述出来,这样一来,我们就把宇宙的状态描述出来了。
我们可以想象,我们能把宇宙的所有可能状态组成一个集合。这个集合用下面一个圆圈表示
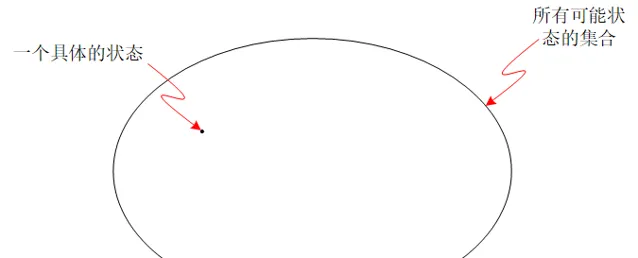
那么,这个「圆圈」所圈定的空间,就叫做「相空间」,这个空间中的每一个点,都是一个宇宙的可能状态。
这种状态,是从微观层面上对宇宙做出的完整描述 - 我们对 每个粒子 的状态都做成精确的描述。宇宙的状态,就是所有粒子状态的集合。每个粒子有三个维度的位置自由度和三个维度的动量自由度。那么宇宙的状态就由6N个变量描述出来(N是宇宙的粒子数目)。这种状态,叫做 「微观态」 。
但是实际中我们对一个系统的描述不可能做到微观层面。这需要太多的数据了。可以粗略估算,1mol的理想气体,如果我们用单精度浮点数来描述这些变量(事实上这是一个相当粗糙的精度!),大约需要1YB的存储空间,是现在全球总存储量的3万多倍!
现实中可行的办法就是忽略具体粒子,只从宏观上对整体状态做出描述。例如说,对理想气体我们不去管里面的每一个分子是怎么运动的,而是只考虑宏观上它的一些统计平均的东西,诸如温度、压力、密度等等。也就是说,我们仅用不到1KB的数据来粗略描述1YB的信息。
这个,叫做「 宏观态 」。
于是,我们就会发现,大量不同的微观态,在宏观上我们是分不出任何区别的。举一个形象点的例子,星爷的满头灰发:

从微观上来讲,我们把他的一根黑发和一根白发互换一下位置,这肯定是两种不同的「发型」。但是从宏观上,我们没有办法区分。当我们说宏观上的「灰发」的时候,我们可能在谈论无数种「微观发型」。我们从宏观上,可能只需要一个变量,「灰度」,就概括了这无数种情况。
一个非常直观,但在统计力学里面极其重要的事实就是, 有些宏观态对应着大量的微观态,而另外一些宏观态,对应着极少量的微观态。
我们还用星爷的头发来说这件事。均匀分布的黑白发,就对应了很多种不同的微观分布:我们可以想想,随便互换一根黑发和一根白发,都不影响「均匀分布」这种情况。但是,如果是这样一种分布:

就完全不同了。这种发型只有一种微观的分布。随便互换一根黑发和一根白发,都会破坏「半边黑半边白」这种发型。
如果黑白发的数量各占一半,它们随机分布的话,显然极大可能出现星爷的灰发,极不可能出现半边黑半边白的头发。前者是极大概率事件,后者是几乎不可能出现的事件。
就像科普书里说的,把黑砂和白砂混合在一起,摇晃两下,我们会发现黑白混合均匀,有可能会出现黑砂全部跑到左边,白砂全部跑到右边的情况吗?有,但是几乎不可能。原因是,均匀混合有无数种混合方式,半黑半白则只有一种。前者是极大概率事件,后者是极小概率事件。
基于这个基本的道理,我们用下面这个著名的公式来定义熵(这大概是一根学者所能想到的最浪漫的墓志铭了)。
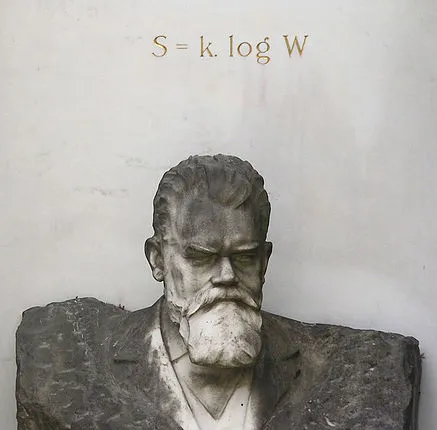
在这个公式里面, S指的是一个宏观态的熵。W指的是这个宏观态包含的微观态的个数 。对一个宏观态而言,它包含了若干种宏观不可辨的微观态。这些不可辨微观态的个数越多,这个宏观态的熵就越大。相应地,如果每种微观态都是随机出现的,那么 熵更大的宏观态出现的概率就越高 。
如果我们数一下一个宏观态中包含的微观态的个数,这不可避免地要用到排列组合的计算。大家知道,排列组合的一个显著特征就是,它的数目是由其中粒子个数的阶乘决定的。也就是说,当粒子数足够多的时候,W将会是一个天文数字 —— 相应地,这里谈论的「更高概率」和「更低概率」的差距也就是天文数字。一个高熵态出现的概率相比低熵态出现概率,何止亿万倍。
也就是说,对于宏观系统(>10^23个粒子), 存在着一种宏观态,其出现的概率远高于其他状态出现的概率 。因为该宏观态所包含的微观态数目远高于其它宏观态所包含的微观态数目。
这个宏观态,就是 平衡态 。也就是熵最大的状态。
我们来举一个简单的粒子。有一箱的理想气体,现在我们把箱子分成相等的左右两部分,那么两部分中的分子数各自是多少呢?如上所述,我们有两种方法来回答这个问题,第一种,就是跟踪每一个分子,诸如「分子1号在左边,2号在右边,……」,这就是微观态;第二中,我们整体描述,「大约有多少比例的分子在左边,多少比例的分钟在右边」,这就是宏观态。
现在我们考虑所有的可能,可以是所有的分子全部在左边,也可以全部在右边,也可以一半一半。总而言之,一共有 2^{10^{23}} 种可能的状态。那么,我们考虑两种极端情况:
1、所有的分子全部在左侧,只有一种分布状态是这种情况。
2、一半在左侧,另一半在右侧。我们可以通过Stirling公式估算出这种分布的可能数目,大约是 \frac{2^{10^{23}}}{10^{11}}\simeq 2^{10^{23}} 种这样的状态。
请停下来,仔细考虑一下第二种情况下的那个数字是什么含义。可以说,它和无穷大的区别仅仅在于,我们还可以用一个数量级来描述它。也就是说,它practically和无穷大没有什么区别。那么,相比于第二种情况(完全均匀的分布),第一种情况(完全不均匀分布)几乎不可能出现。
那么,我们回到前面的相空间话题。相空间包含了所有可能的微观态。从上面这个论述中可以看出,在这个空间中,绝大多数的微观状态对应着平衡态。也就是说,基本上整个相空间都被那些高熵态填满了。低熵态几乎不占体积。形象地比喻一下, 低熵态的体积就是在整个宇宙中的一粒尘埃 - 这个比喻只是形象,并不准确。事实上,低熵态的体积比「尘埃」还要小的多的多。
或许我们可以借用彭罗斯的插图来表示这种情况 [2] :
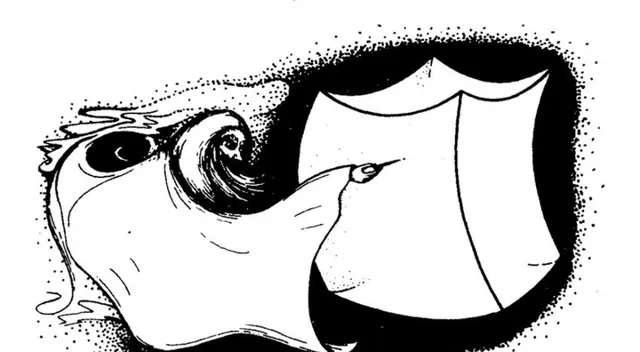
这张图说的是,只有上帝才能用它那极细小的针头点到那个几乎不可能出现的那个状态。
宇宙的演化,就是宇宙状态随着时间的变化。用我们前面那张形象的圈图表示,它的整个历史线就在相空间中划出一条 轨迹(动力学中把它叫做trojectory) 。
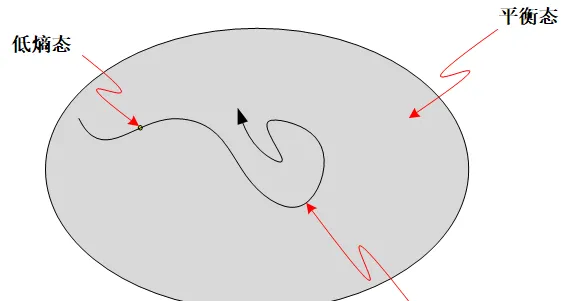
那么我们现在可以来看时间箭头的问题了,我们来打一个比方,比如说你现在处在一个黑暗的外太空,没有任何条件限制你往哪边走。你可以往前,也有同样的自由往后。你可以说你的运动是对称的。
整个空间只有你的身边有一盏灯并且这是宇宙中唯一的一盏灯,灯很小,发出一点点微光。

现在你开始向着某个方向走。
这时候我来问你,你对你的未来的亮度有何预测?
这是个简单到令人发指的问题,你用头顶的那一根珍贵无比的头发丝想一下都知道答案:你的未来亮度一定是变暗的。虽然没有人限制你往哪个方向走,但是问题是基本上所有的方向都是变暗的。
这盏小灯,就类比了相空间中的低熵区。我们由此可知,这个粒子无论如何,最终几乎必然向高熵演化 —— 历史与未来是不对称的。原因是,相空间中高熵区和低熵区是不对称的。这和粒子自身的运动方程是不是对称的没有关系。
说到这里,似乎都很完美。但是,故事并没有结束。
1.2,初始条件问题
从前面的讨论,我们可以得到一个结论,高熵是极高概率的,低熵是极低概率的。但是如果我们仔细分析这个结论, 我们能得到时间箭头的合理解释吗?
答案是不能。
因为从上面的论述中,我们只能得到这样一个结论,「 如果我们现在处于低熵区 , 那么后续 我们几乎必然向着高熵区演化」。请注意黑体的部分,我们从熵的统计解释到时间箭头之间,多了一个前提条件:「如果我们现在处于低熵区,那么后续……」。
而这个多出来的前提,则是一个麻烦制造者。
首先,既然前面分析了,低熵区是一个极端不可能的状态,那么按理说我们就极端不可能处在现在这种状态。在相空间中几乎所有的演化规矩 —— 也即是最可能发生的演化 —— 是从高熵区向着高熵区演化 —— 也就是说,熵不变。
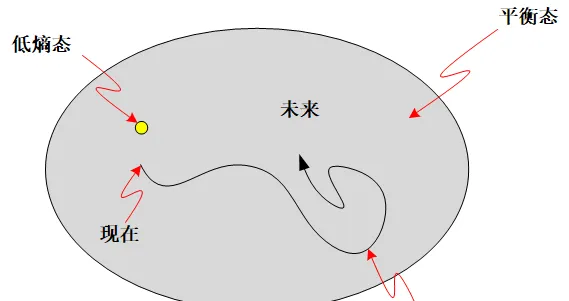
而我们现在谈论的,却是一种极端的情况,我们把演化的出发点限制在一个非常极端的位置(请注意下图中低熵区的画法是极度夸张的,它根本就没有那么大):
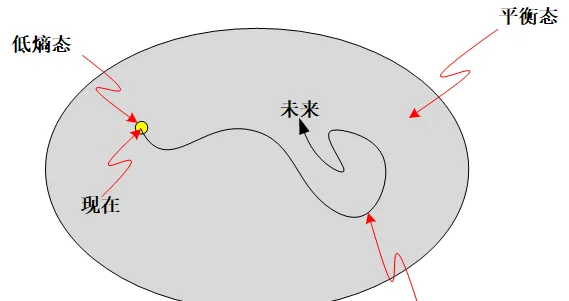
好吧,你可以说,即使是极端不可能出现,可是我们的的确确恰好处在一个极端状态啊。这是一个简单事实。
所以,我们等于在说,「由于我们现在处于低熵态,所以未来更可能向着高熵态演化」。这个从逻辑上很简单。但是对时间箭头这个问题来说,就比较尴尬。我们现在预设了时间序列的一端是低熵,那么另一端是高熵就不言而喻了 —— 高和低总是相对的嘛。
这个回答其实就是预设了时间箭头的存在,来解释时间箭头。因为我们假定的前提就是,我们的起点是一个特殊的点。也就是说,我们指定了「现在」的特殊,以及未来高概率的「普遍」,来解释现在和未来的不对称。
为了把这个矛盾放大,我们可以用同样的逻辑来回溯历史:「假设我们现在是低熵,那么历史上宇宙从何而来?」
因为宇宙极大概率是高熵的,所以这个问题的答案就是,极大概率上,历史也是从高熵而来。也就是说,历史上极大概率是熵减 —— 即历史上「 时间箭头是反向的 」。
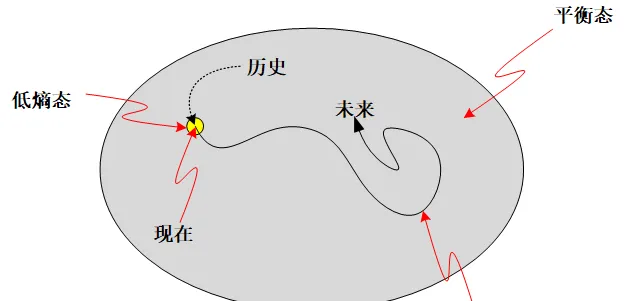
如果我们要保证我们的时间箭头总是「朝前」,我们就需要假定历史上它是从更低熵演化而来。那么历史的历史上它就从更更低熵而来……,然而熵是有下限的——也就是零。我们这么追问下去, 就追到宇宙的起点了: 宇宙必然是从一个极其低熵、极端不可能的情况出现。
为了使我们的时间箭头有意义,我们得到了「宇宙起源于一个极端情况」这种结论。 这几乎就是赤裸裸地先打靶后立靶 (beg the question) —— 如果我们不能从其它的地方来justify「宇宙起源」这个问题的话。
这就是 宇宙学箭头 。但是这里我不打算就此展开,因为首先它还有很多争论,其次我也不是宇宙学的专家,说出来的话几乎必然是错误的。
我们可以弱化我们的讨论,不论如何,现在的一个简单事实就是,我们是一个低熵宇宙,所以未来它向着高熵宇宙演化就是自然而然的结论,所以现在我们感受到了时间箭头。
这就是初始条件问题。
总而言之,前面两个问题,一个指出,「存在着一些极端的情况」,另一个指出「我们现在就是一种极端情况」。两者结合,才能得到时间箭头的解释:未来高概率是一种普遍情况,当然和现在我们的极端情况不是对称的。
时间不对称,是因为我们本身就问了一个不对称的问题。
2、「无知」的野蛮生长。
前面说的是一种大家最常用的熵的统计诠释,玻尔兹曼熵。
但是,统计力学的基础问题其混乱程度,远远高过其它物理学分支,量子力学虽然争论良多,但是至少还有一套统一的「正统」形式理论。统计力学其众说纷纭的程度则更甚。这里我们还可以从其它角度来阐述热力学箭头。
比如说吉布斯熵。 如果说玻尔兹曼熵说的是状态的体积,吉布斯熵说的就是状态的密度 - 它的概率密度。如果说我们谈论平衡态,对应着同样的宏观性质,这两者是有一一对应关系的:的确,密度越高,则体积越小嘛。也就是说,在这种情形下,它们是等价的。
但是在多数情况下, 吉布斯熵和玻尔兹曼熵其实是不等价的 。吉布斯熵和玻尔兹曼熵的区别就在于,在玻尔兹曼熵中,我们对一个 确定的宏观状态 下,来计算所有能够表现为这种宏观态的微观状态的数量。但是对吉布斯熵而言,我们对微观态的计数范围,是从某个 特定初始条件 (范围)出发、演化所能到达的所有可能状态。两者的计数范围都不同,当然计数的结果就不同。严格讲,它的计数范围要比玻尔兹曼熵小得多:因为它受到初始条件的限定。
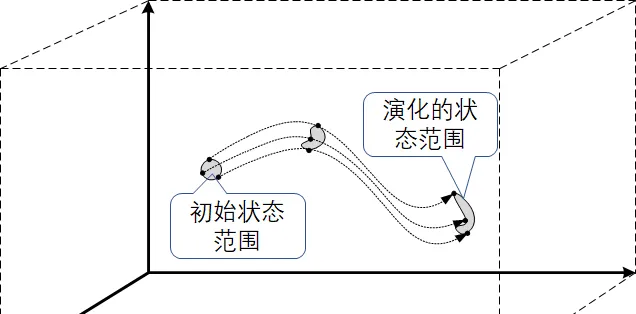
这会给吉布斯熵带来很多优点,例如说它不要求等概率、不要求平衡态等等。但是,如果我们计算吉布斯熵的演化,我们会发现它是 守恒 的。也就是说,根本就不存在熵增!所以,严格讲,吉布斯熵其实是时间对称的。这其实很容易理解,因为它的演化是从严格的微观动力学推演的。 微观动力学的对称性就决定了吉布斯熵的对称性 。
那么,吉布斯熵的统计力学描述,岂不是和热力学熵不一致了吗?它并不能给出熵增的结果啊。
答案在于「 粗粒化 」。我们对任何系统的任何观察,都不可能是100%精确的,我们观察的结果,都是一个大致范围。比如说一个人身高175.5cm,其实一般的测量精度给出的,大约是在175~176之间的范围。也就是说,我们日常经验到的世界,都是粗粒化的。
比如说,我们对系统的初始状态指定一个概率分布(一个初始粗粒)。这个分布的体积越小,就越精确,也就意味着我们对它的认知就越确定。
但是,随着系统的演化,这个概率分布就会发生各种形变。由于运动方程本身的时间可逆性,这个分布的 体积不会发生变化(也就是熵守恒) 。但是它的形状却会越来越复杂。运动方程的非线性就决定了,它会演化成一种 分形结构 。下图形象化地描述了分形的特征。一个很小的初始粗粒可以被拉长成任意长的纤维(理论上的确可以是 任意 长的),然后编织起来团成一个线球塞满整个相空间。在一个可以 无限精度观察 (细粒化)的观察者看来,无论它是如何塞满相空间的,它的体积不变:也就是概率分布是不变的,即熵守恒。线球再大,其内部基本上都是空隙。但是对一个粗粒化的观察者看来,当这个线球精细到一定程度,我们就只能看到一只球,我们无法分辨任意细的纤维。我们队它的精细结构的知识就丢失了,因而它的体积似乎是扩大了。

也就是说,当我们不去精确追踪系统的演化,而是为演化设定一定的精度(相空间粗粒化),我们会发现我们对系统越来越无知,我们对系统的确定性越来越丧失了。
那么,随着系统的演化,我们对系统的知识不断地丢失(因为相空间结构的精细化)。这就是熵增。从这个角度上看,熵并不是我们科普语言中的「 混乱度 」而是我们的「 无知度 」。这就是1970年代发展成熟的熵的主观诠释(主要来自Jaynes的工作) [3] 。简言之:
因为我们无法精确跟踪系统的演化(基于系统演化的混沌特征),所以我们对系统的无知程度不断增加,这就是熵增。
统计力学本身就是粗粒化的学问。 如果我们能精细了解系统的运动,就没有任何统计力学的生存空间。
那么当我们谈论一个系统的熵的时候,首先要问的问题是,你用何种精度的自由度来定义成你的热力学系统?你的知识,决定了熵的大小。故而, 熵就是你对系统的无知程度, 也就是你对系统信息的掌握程度。如果我们做不到无限精度,只要对系统有一点点的无知,这种无知就会随着时间迅速地野蛮生长(事实上,是指数速度生长)。于是很快地,我们就丢失了我们对系统的所有细节知识,只留下了了几个宏观量的认知 —— 这就是平衡态。
于是,我们把我们能相对确切认知的那一端,叫做历史,把我们无法确切认知的那一端,叫做未来。这就是一种非常符合直觉的时间箭头了。
关于相空间、演化、混沌、分形等的进一步讨论,请参考本人专栏:
3、一点点量子调味品
当我们开始考虑量子力学的时候,一定要小心翼翼。量子力学和经典力学有着非常本质的区别,很多时候我们容易把它们混淆起来。例如说,用量子不确定性来解释熵,这中间陷阱重重。很多哪怕是专业人士,都容易落入其中
我们来考虑前面提到的「线团」的类比。这是一种分形结构,它的特征就是无限精细。但是,还有一个关键因素,就是它的形成依赖于非线性演化。不仅如此,混沌系统的最基本特征,对初始条件的极端敏感(SDIC)也依赖于非线性演化。
然而量子力学是线性的。
如果我们用不确定原理来讨论问题,就意味着我们用量子力学来处理问题了。那么我们就要改用薛定谔方程而不是哈密顿方程。那么混沌就失去存在基础了,因而就没有前面所说的那种精细结构,因而不确定原理也就不能成为粗粒化的理由。这就是为何Robert Bishop说:
Quantum chaos, or quantum chaology as it is better called, is the study of the relationship between chaos in the macroscopic or classical domain and the quantum domain. [4]也就是说,大家对量子混沌的研究,其动机并非因为量子中存在混沌现象,而是要寻找经典混沌的量子起源:为何一个不能容许混沌现象的底层理论在宏观上产生了混沌现象?其根本就是 量子-经典过渡问题。
所以说,在量子领域中,真正的问题就是这个量子-经典过渡问题,也就是所谓的「波函数坍缩」问题。用不确定原理在经典混沌理论中的解释是无效的。
谈论量子理论,我们应该首先明确一点, 量子力学和经典力学一样,也是时间对称的。
在「 正统」诠释里面 ,这似乎不对。「波函数坍缩」似乎不是时间对称的。对一个已知量子态,我们的观测结果就是某一个本征态,它出现的概率就是由波恩规则决定的、不可预测的。按照前面「熵即无知」的解释,我们在没有看到结果之前对它确实是无知的。难道观察行为不会造成熵增吗?
这个问题就比较微妙了。
如果我们用冯诺依曼熵来做一个计算,我们的确会得到这样的结果:对一个纯态进行观察的前后,熵是增加的(对一个混合态的观察会复杂一些,这里就略过)。也就是说, 波函数坍缩看似的确引发了冯诺依曼熵的熵增 (我们这里暂时不去讨论「坍缩」这个概念本身是否有效)。那么这是否就是热力学熵增的起源呢?
对此我们还是怀有疑虑的。量子熵增和经典的熵增很不一样。在经典力学里面,我们的无知指的是「系统的状态在那儿,我们不知道确切的状态为何」,而在量子系统中,则是「我们知道系统的量子态,对一个观察结果我们不知道」。
也就是说,在量子力学里面我们通常讨论的观察问题,其实也是在问一个不对称的问题:
「已知量子态,我们会得到何种观察结果,它又会坍缩到哪一个本征态?」。
这里我们假定了一个 初始的纯态 作为前提,也就是限定了初始态为确定的量子态。
和前面类似地,我们不妨反过来问:
「现在我们通过观察得到了一个确定的观察结果,那么历史上它从何演化而来?」
我们知道量子力学的常规应用是已知历史知识,我们用它来预测未来。那么这个问题则是,已知未来,我们如何用它来反推历史?这个问题并不难,通过概率论的基本原理和薛定谔方程,我们的确可以反推历史。结果很有意思,也就是说,我们对历史的反推得到的和对未来的预测结果完全相同!也就是说,从这个角度上说,即使是坍缩过程,也是时间对称的。这个就成为所谓的「 Two state vector formalism」(TSVF,双态表述) 的来源 [5] 。在这个理论中,向前的演化和向后的反向演化共同构成了一个系统量子演化的全部信息,它是完全时间对称的。
更加重要的是,关于「坍缩」,现在越来越多的人相信,它只是一个方便的工具,而不是真实存在的物理过程。这就是以多世界理论为代表的所谓的「纯幺正量子力学」的主张。如果没有了坍缩,量子力学就是一个纯幺正的演化,当然是完全时间对称的。对一个纯态而言,无论如何,它的冯诺依曼熵总是保持为零。
那么,熵增是如何来的呢?
这就需要我们掰开了揉碎了把「坍缩」这个概念搞清楚。这里空间太小我写不下,但是还是可以大略描述一下。
观察意味着纠缠,纠缠意味着不可分割 。而不可分割就意味着「整体>所有部分的加和」。这就是著名的subadditivity:
S_{AB}\leq S_A+S_B
也就是说,当我们用一个仪器完成了对系统的观察时,我们并没有「坍缩」掉系统的量子态。我们只是使仪器和系统互相纠缠起来了而已。此时,如果我们分析(系统+仪器)这个复合系统,我们必然会得到熵仍然为零的结论。但是,如果我们单独观察系统和仪器,然后把它们加起来,我们就会得到熵增的结论(也就是「坍缩」的结论)。 那部分额外的熵从哪里来?就是从我们忽略掉的仪器和系统之间的纠缠信息而来。
事实上,从退相干的角度,所有这些都是可逆的,理论我们完全可以逆转一个「坍缩」,从而回到初始状态。但是实际上这是不可能的。 因为系统无时无刻不在和环境发生纠缠,和整个宇宙发生纠缠,乃至于这些纠缠信息扩散到整个宇宙当中。而我们无法对整个宇宙完成观察!这就解释了为何我们对系统的知识总是在减少 - 也就是说熵总是在增加。
而「和整个宇宙发生纠缠」意味着什么?意味着多世界理论中的「世界分支」。也就是说,在多世界理论中,熵增总是可以跟越来越多的世界分支联系在一起。
这一切看起来很美好,然而,其实这只是我暂时的一厢情愿。因为科学家们并没有就「坍缩」这个问题达成共识。
4、假如「时间倒流」
我以前回答过一个问题,
我的答案是:一个熵减的世界大概和我们现在的世界没有什么不同。
这个回答可能和绝大多数人直觉中的答案完全相反。毕竟,物理学最基本的定律之一,热力学第二定律,如果是完全逆转的,怎么可能整个世界还会是一样的呢?
因为不论是熵增还是熵减,都是时间序列的不对称。只是「未来」和「历史」调换了一下而已。
而底层的物理定律毕竟是可逆的。
那么这时候,我们可以来想象一个熵减的世界了。我们只需要把所谓的初始条件问题改为末态条件问题就好了。解过微分方程的人都知道,这两者在数学上毫无分别。就好像我们对自由落体过程的时间序列两端做出不同的定义,并不会改变它的物理合理性一样(因为自由落体和竖直上抛都是物理上合法的运动),无论是初始条件还是末态条件对我们而言,其实物理合理性不会有什么不同,甚至我们可能压根儿就无法觉察我们的世界现在是「熵减」的 —— 因为我们会习惯性地把熵减世界中的未来当成「历史」。
这里我们回到了文章最开始的声明:我这里谈论的所谓时间流动,并不是一个真正存在的正在流动的东西,而是时间维度上物理现象的不对称性。
从物理主义的角度,一个脱离于物理过程的时间箭头是没有意义的。 我们所体验的,不是时间本身的箭头,而是物理过程在时间维度上的不对称性 :时间,就是微分方程中的那个与实数轴同构的「t」。这个「t」向着两端任意延展,但是这两端的物理图景有着不同的结构。一端,是确定的,「低熵的」;另一端,是不确定的,「高熵的」。 我们是用熵增的方向来定义了时间的方向,而不是沿着一个预设的时间方向发现了熵增。 从这个意义上讲,考虑「熵减」并不是物理的,而是语义学的。热力学第二定律说的,其实也不是熵增,而是熵在时间轴上的不对称。
我们不妨这样想象我们的一生。如果我们把时间反演,我们将会从骨灰盒里爬出来,变成老人,越来越年轻,最终变成小孩,再爬回娘胎,变成受精卵,然后变成了一些蛋白质和核酸。我们会感觉有何不同吗?其实不会的。 如果我们假设我们的整个意识状态都是由物理定律决定的,那么由于物理定律本身的对称性,时间反演中,我们自身的记忆也会随之原样不变地反演回去。
比如说,我现在处于不惑之年,我有的大脑中存储的记忆包含了一系列事件的序列:从一端的童年、少年、恋爱、大学、结婚、工作、生女,一直到另一端的端点:正在写一篇关于时间箭头的文章。我们说,如果时间是「正流」的,这段记忆毫无问题。但是假如时间倒流,我从骨灰开始返回到不惑之年,我的记忆仍然原封不动地回到这个状态,这才是符合物理定律的。我的记忆中不会出现退休、女儿结婚、抱外孙、弥留这段历史,因为这才是不符合物理定律的。
那么,不论是「正流」还是「倒流」,我现在的记忆状态不会发生什么变化。 在熵减的世界中,我们记住的是「未来」,而不是「历史」 。或者说,这仅仅是一个semantics:我们把历史称作未来,把未来称作历史。如此而已。

从心理学时间来看,我们其实并不知道过去发生了什么,也不知道未来将要发生什么,我们只知道 现在我们的记忆状态 是什么。而记忆是什么?记忆是我们观察者的存储器在「历史」上与外界发生相互关系,造就的它「现在」的物理状态。 我们回忆过去,就是在体验我们存储器中现在的状态 – 是从现在的记忆状态「反推」出来的历史状态。 然而,我们回忆「过去」,从物理定律上来说,也是在回忆「未来」 – 只不过我们把这种回忆叫做「期望」。
也就是说,当我们回味着我们的记忆的时候,我们所能区分的其实不是一个 纯粹本体论时间意义上 的绝对的历史与未来, 我们所能区分的,是两个相反的时间方向 。正是由于熵增的存在,使得其中一个方向是确定的、唯一的,而另一个方向则是不确定的、开放的。只不过,我们把确定的那一端称为历史,把不确定的那一端称为未来。
真的有一个「流动」的时间吗?这其实不重要 。除非「时间」这种东西有一种可以超出物理过程而对我们产生真实影响的机制 —— 但是那样一来,时间也就至少是物理现象之一、并且也满足物理定律了。
一个流动的时间存在并切实影响了我们的心理?还是说它只是幻象,真实存在的是一段连续的不对称序列,我们naively地把确定的一端称作历史,把不确定的一端称作未来?这个问题一直萦绕着我。我其实不知道答案。
5、一点点哲学调味品
现在我可以稍微谈一下,为何我会避免谈及一个「真实」的、「流动着」的时间,而更愿意讨论直接的物理现象在一个时间维度上的序列。
最直接的原因就是,物理现象是可描述、可计算的,并且能够对我们发生直接影响的。而脱离物理现象的一个本体论意义上的时间,则更像是一个哲学概念。
即使是在哲学上,相比于「时间维度上的序列」而言,「时间流动」这种图景存在着某些难以理解的问题。
首先,我们可以问这样一个问题,既然时间在流动,那么它的流速是多少?
这个问题多少有些尴尬。一般而言我们谈论某种事物的「流速」,我们必须要用时间来度量它。比如说n米/秒,或者是n℃/秒等等。现在我们谈论时间的流速,本身暗示了一种自我嵌套,似乎唯一的答案就是1秒/秒?或者是是1?这是什么意思?「当时间过了1秒钟,那么它过了1秒钟」,这句话根本就不提供任何信息。既然它不能提供信息,那么定义这个「流速」就是完全冗余的。
我们还可以问另外一个问题,既然时间在流动,那么它有某种性质是在变化的。那么到底是什么性质在变化?again,当我们谈论「变化」的时候,我们是预设了时间的。但是当我们谈论时间本身的变化,就无法处理了。
对时间这件事最著名的哲学分析是McTaggart关于A理论和B理论的论述。这些讨论出现在两篇巨著中,一个是1908年的「The Unreality of Time」, [6] 一个是1927年的「The Nature of Existence」 [7] [8]
关于这一点,请参考我以前的答案
参考
- ^ Carroll, Sean (2010). From Eternity to Here: The Quest for the Ultimate Theory of Time. ISBN 978-0-525-95133-9
- ^ 彭罗斯,1989,皇帝新脑
- ^ E. T.Jaynes, 1965, "Gibbs vs Boltzmann Entropies" American Journal of Physics 33, 391 (1965); doi: 10.1119/1.1971557
- ^ SEP 词条「chaos」
- ^ arXiv:0706.1347v1
- ^ J. Ellis McTaggart. 「The Unreality of Time.」 Mind 17, no. 68 (1908): 457–74.
- ^ The Nature of Existence (Volume I), 1921. Cambridge: Cambridge University Press.
- ^ The Nature of Existence (Volume II), 1927. Cambridge: Cambridge University Press.










