我试着证明一下......
题主所说的2048游戏,有的格子是4×4的,有的是5×5的,这里我们拿4×4举例。

我们首先想这么一个问题,要想凑齐2的n次方(n>0), 最少 需要几个格子。
显然,2的一次需要一个格子,2的2次需要2个格子,那2的3次呢?(只考虑基数是2,忽略可能出现的4的情况)
很容易想到4个格子的可能性,然而事实上,存在一种3个格子即可凑出8的可能性。
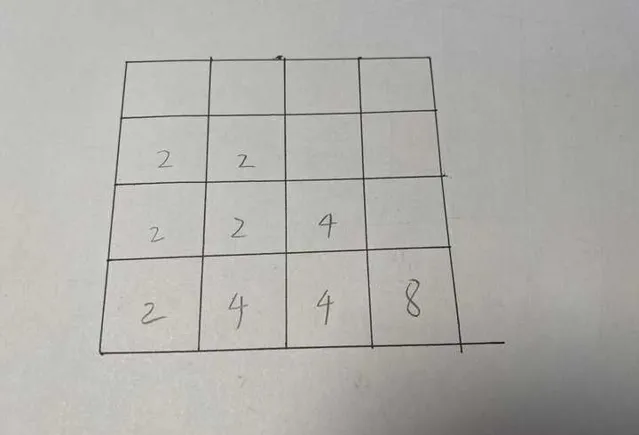
那么,2的4次呢?很容易联想到,需要4个格子。
因为要凑出2的3次需要3个格子,而我们把其中一个2的3次放在那里,再去凑一个2的3次,又需要3个格子,总共花费4个格子,如此类推,2的n次最少需要n个格子。
所以,在4×4的格子中,理论上最多达到2的16次。
而在n×n的格子中,理想情况下最多达到2的 n^2次
证完。









