先问是不是,再问为什么。
球的体积公式 \frac43\pi r^3 ,对 r 求导确实可以得到球的表面积公式 4\pi r^2 。
但是 谁又规定了球的体积公式必须得用 r 作为自变量呢 ?考虑用直径作为自变量的体积公式 \frac\pi6d^3 ——实际上在工程学语境下这个还要更常用一些,因为直径比半径好测量——对 d 求导得到的是 \frac\pi2d^2 ,而不是表面积 \pi d^2 。或者更过分一点,考虑用表面积作为自变量的体积公式 \frac{S^\frac32}{6\sqrt{\pi}} ,对 S 求导之后得到 \frac{\sqrt S}{4\sqrt\pi} ——更不知道跑哪儿去了。
可见,「体积求导等于表面积」成立与否,至少要取决于「体积公式中使用的是哪个量」,而不只是取决于「是什么几何体的体积」。
那么球的半径比起其他的量又有什么特殊的呢?
要回答这个问题,不妨先看看导数的定义。不严格地来讲,导数(导函数)的定义就是因变量随自变量的增长率,或者说因变量「极微小变化」与自变量「极微小变化」的比值。那么我们考虑一个球和与其同心的一个稍微大了一点的球,这里的因变量——体积——的「极微小变化」就是多出来的那一层壳儿的体积。
这层壳儿的体积该怎么算呢?我们想象这个壳儿是由很多很多稍稍弯曲的瓷砖拼接成的(可以想象一个球形的建筑穹顶,天文台或者东方明珠电视塔那种的),不难发现每块瓷砖的高度就是壳儿的厚度,而所有瓷砖的面积之和就是球的表面积。因为一个球只是比另一个球稍微大了一点,这个壳儿也是非常薄的,每块稍稍弯曲的瓷砖就几乎是一个没有弯曲的柱体,所有柱体的底面积之和就是球的表面积,高则是壳儿的厚度。换句话来说,因变量的「极微小变化」和壳的厚度之比就是球的表面积了。而壳的厚度——不难发现——正是两球的半径之差,也就是半径的「极微小变化」(而不是直径的);因此,体积的「极微小变化」和半径的「极微小变化」之比可以得到表面积。
总之,之所以只有对半径求导才得到表面积,就是因为球和稍大的球之间那层「壳」的厚度正是半径的差值。此外,题主也提到了对圆来说有类似的关系;分析一下不难发现,两个同心圆之间「壳」的厚度也同样是半径的差值。
那么对于其他的可以构造出「壳」的图形,也有类似的关系吗?
我们可以试试看。
比如正方形,大正方形和小正方形同心摆放,不难看出壳儿的厚度是「半边长」的差值。设正方形的「半边长」为 x ,则面积为 (2x)^2=4x^2 ;求导得到的 8x 也正是正方形的周长。
当然,两个同心摆放的立方体也完全类似,会得到厚为「半棱长」差值的一层壳儿。设立方体的「半棱长」为 x ,则体积为 (2x)^3=8x^3 ;求导得到 24x^2=6\cdot(2x)^2 ,也正是立方体的表面积。
这样听起来,就有一个很诱人的结论摆在我们面前——
——椭圆和稍大的椭圆之间也是一层「壳儿」,那么对椭圆的面积 \pi ab 求导,似乎就可以得到著名的无法简单表示的 椭圆周长 了。比如,考虑离心率 \frac{c}{a}=0.6 的椭圆,就有 b=0.8a ,椭圆面积就是 0.8\pi a^2 ,周长是否就是 1.6\pi a 了呢?
这种好事自然是不存在的——相信有的读者已经看出了个中原因:将两个同样离心率的椭圆同心重叠得到的「壳儿」厚度并不均匀,只有在长轴端点附近厚度才是 a 的差值,在短轴端点附近厚度就只有 b 的差值那么厚了。
因此,前面的结论还需要改良一下: 若两个体积相差很小的同种图形/立体,其面积/体积之差可表示为一层 厚度均匀的 「壳儿」,且这个「壳儿」的厚度能表示为某个长度的差值,则面积/体积对这个长度的导数就是这种图形/立体的周长/表面积。
这里再举一个例子。考虑下图中的任意三角形 \triangle ABC 及与其相似的大一圈的三角形 \triangle A'B'C' :
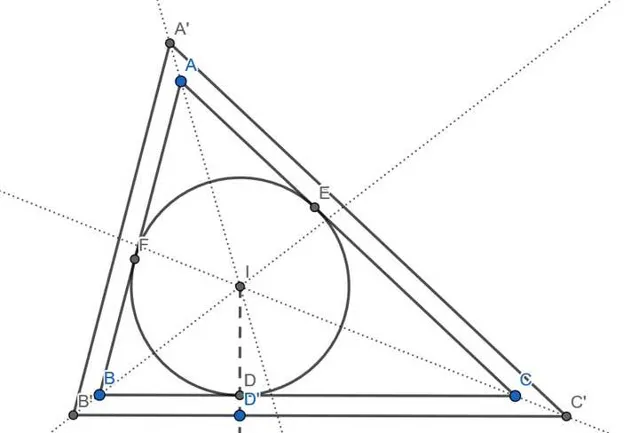
从图中不难发现,三角形的内切圆半径 r 正是我们要找的那个「差值等于‘壳儿’厚度」的长度。
那么为了用 r 表示 \triangle ABC 的周长和面积,不妨设 \begin{cases} \angle BAC = 2\alpha \\ \angle ABC = 2\beta \\ \angle ACB = 2\gamma \end{cases} ,则有
\begin{align} S_{\triangle ABC}&=\frac12AB\cdot r+\frac12BC\cdot r+\frac12CA\cdot r\\ &=\frac r2\left(\frac r{\tan \alpha}+\frac r{\tan \beta}\right)+\frac r2\left(\frac r{\tan \beta}+\frac r{\tan \gamma}\right)+\frac r2\left(\frac r{\tan \gamma}+\frac r{\tan \alpha}\right)\\ &=r^2\left(\frac1{\tan \alpha}+\frac1{\tan \beta}+\frac1{\tan \gamma}\right) \end{align}
以及
\begin{align} C_{\triangle ABC}&=AB+BC+CA\\ &=\left(\frac r{\tan \alpha}+\frac r{\tan \beta}\right)+\left(\frac r{\tan \beta}+\frac r{\tan \gamma}\right)+\left(\frac r{\tan \gamma}+\frac r{\tan \alpha}\right)\\ &=2r\left(\frac1{\tan \alpha}+\frac1{\tan \beta}+\frac1{\tan \gamma}\right)\\ \end{align}
显然前者对 r 求导即可得到后者。
再举一个三维的例子。考虑棱长分别为 a,b,c 的长方体,给它增加一层厚度为 d 的壳儿之后棱长就会变成 a+2d,b+2d,c+2d 。由此可见, \frac a2,\frac b2,\frac c2 这三个量在变化前后的差值都等于壳儿的厚度。因此,不妨令 \frac a2=x ,再将 \frac b2,\frac c2 分别表示为 x+\frac{b-a}2,x+\frac{c-a}2 ,这样三棱长就都以「差值等于壳儿厚度」的 x 表示出来了。(注意,由于 x 的增加量是壳儿的厚度,不可以将 \frac b2 表示为 x\cdot\frac ba ,否则 x 变化时棱长的变化量就和 x 的变化量不同,也就无法使用上面的原理了。此外,为了进一步表明 x 变化时 \frac{b-a}2,\frac{c-a}2 不应该随之变化,也为了简化推导步骤,下文设 y=b-a,z=c-a 。)
那么,用这个表示法求一下长方体的体积和表面积:
\begin{align} V&=abc\\ &=2x(2x+y)(2x+z)\\ &=8x^3+4x^2(y+z)+2xyz \end{align}
\begin{align} S&=2ab+2bc+2ac\\ &=4x(2x+y)+2(2x+y)(2x+z)+4x(2x+z)\\ &=(8x^2+4xy)+(8x^2+4x(y+z)+2yz)+(8x^2+4xz)\\ &=24x^2+8x(y+z)+2yz \end{align}
不难看出体积对 x 求导仍能得出表面积。
至此,「均匀壳儿差原理」(暂定名)应该可以说相当牢靠了。球的表面积也只是这个原理的一个实例。
嗯,这很好,那么这严谨吗?数学吗?
——突然想自辩两句了。
其实我在知乎上回答偏数学的问题的时候,一般都绝不会把严谨性放在首位,而是把「建立思路」或者「建立正确的直觉」放在首位。我个人在看其他回答的时候也更喜欢那些有助于建立正确的直觉而不只是shut up and calculate的,若是看到一句解释也没有的纯计算回答(这样的回答还挺不少的),更是容易一口气捯不上来。不是说写积分式不好,但写了积分式却不说为什么积分式能解决问题,在我看来很可能实在帮不上这些问题的题主(否则题主为什么不直接问某个积分怎么算呢?)。
但「论证的时候只提直观不提严谨性」不代表「论证无法严谨化/公理化/形式化」。就说说这次的这个「均匀壳儿差原理」吧—— 若两个体积相差很小的同种图形/立体,其面积/体积之差可表示为一层 厚度均匀的 「壳儿」,且这个「壳儿」的厚度能表示为某个长度的差值,则面积/体积对这个长度的导数就是这种图形/立体的周长/表面积。
接下来,把这段话变成「数学语」。
(高中同学请注意:
如果这里的「函数」是电势的相反数 -U ,那么某点处「函数的梯度」就是电场强度 E ,大小与 U 下降的「速度」成正比,方向沿着 U 下降的方向,即 -U 上升的方向;
如果这里的「函数」是高度 h ,那么某点处「函数的梯度」大小是这一点最陡的坡度(即倾角的正切 i=\tan\theta ),方向是沿着最陡的坡向上。
简而言之,梯度就是一个方向沿着变化最快的方向向上、大小与变化率相同的东西。)
而「厚度均匀」这个条件,想想看「等高线均匀」意味着什么也就容易明白了—— 各点的梯度大小相同 。
那么万事俱备,「均匀壳儿差原理」终于可以变成「数学语」了: 对于梯度大小恒定的函数 f ,有 \frac{\mathrm d\left(\int_{f\leqslant r}\mathrm dV\right)}{\mathrm d\frac{r}{|\nabla f|}}=\int_{f=r}\mathrm dA 。 这其实就是更具一般性的 余面积公式 (coarea formula)的一个特殊形式——其他答主也指出了这一点。(若对不均匀的壳儿考虑「体积的微小变化量等于壳儿厚度在整个表面上的积分」,通过这个思路甚至可以导出余面积公式的一般形式;不过此处暂且按下不表。)










