安利一本线性代数 魔法书 。
叫做【沉浸式线性代数】(Immersive Linear Algebra) 。
里面的图像都是活的 ,能按照你喜欢的姿势动,可以全方位观察,有助消化艰难的理论。

这免费书在Hacker News获得了 1200+ 的高热,并引起了一阵「好人一生平安」的感激之情。
图像都能怎么玩? 我们一步步看。
打开你的魔法书
来看第三章 向量点乘 (Dot Product) 里的一个栗子:
复习一下「投影」。你看,有一束光打在三角形上。然后,三角形背后的「桌面」,留下了它的影子。
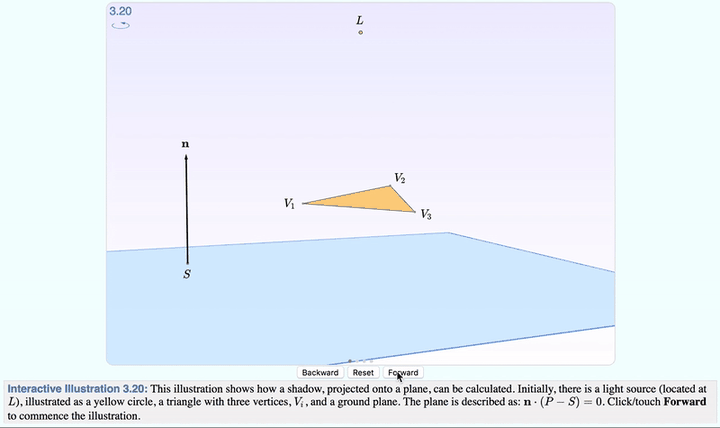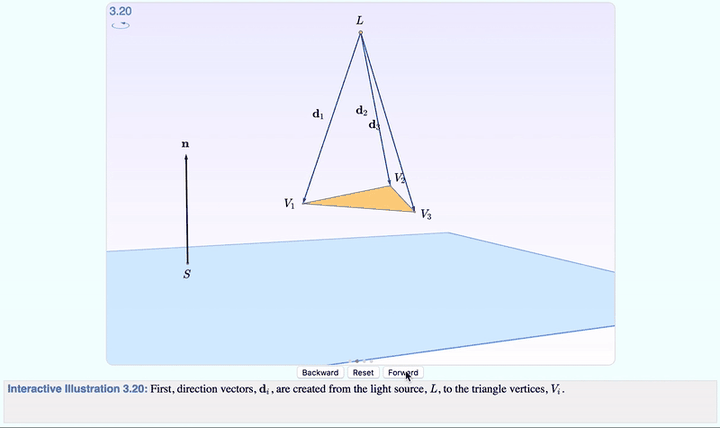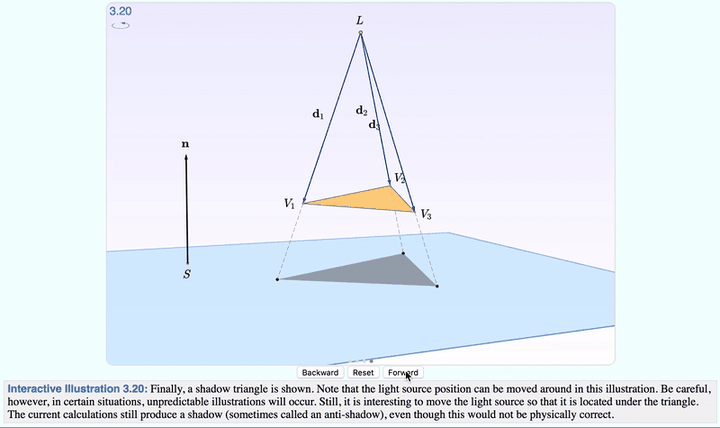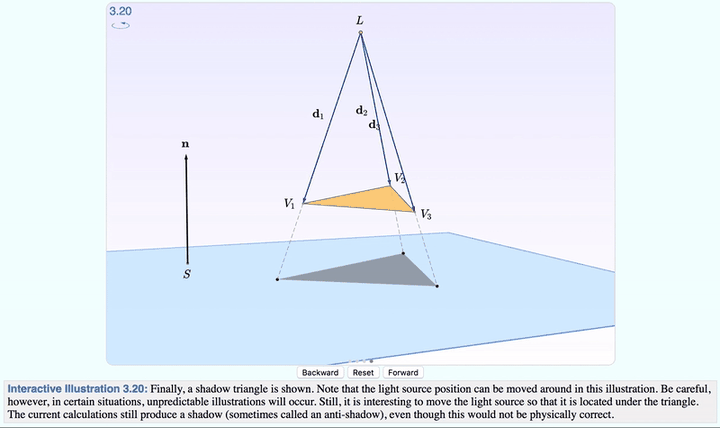
点击 Forward ,就可以分步观察,从光线发射到生成影子的全过程了。
图像变化的时候,下面的 文字解释 也会变,每一步要注意什么,都写在里面。
如果你感觉3D图像更生动,只要点左上角的 旋转按钮 ,图像就会转起来了。
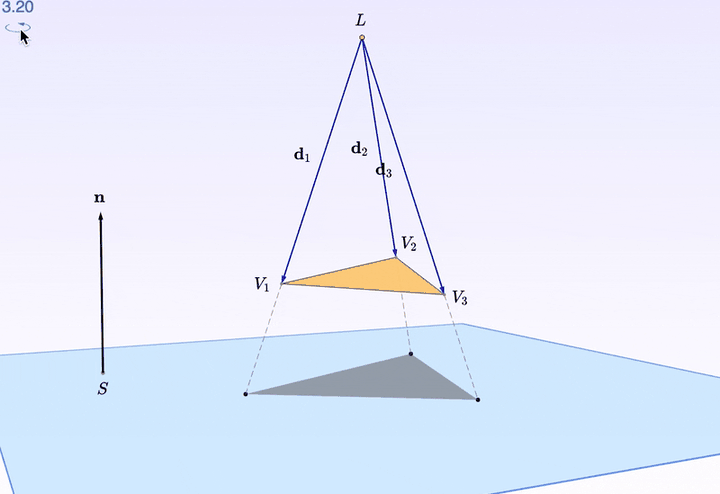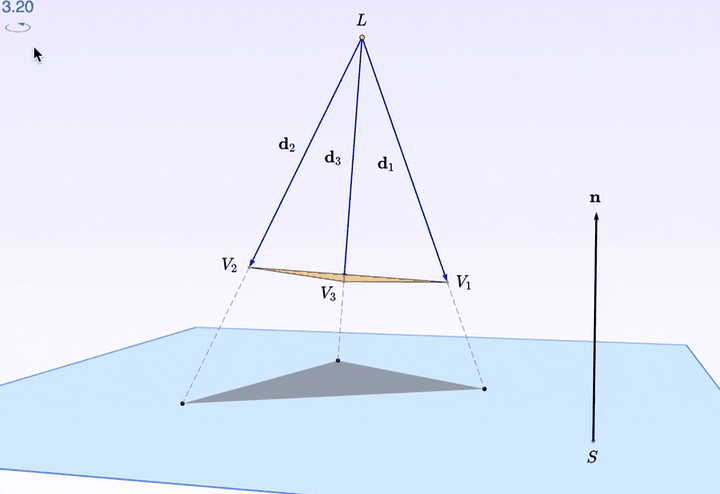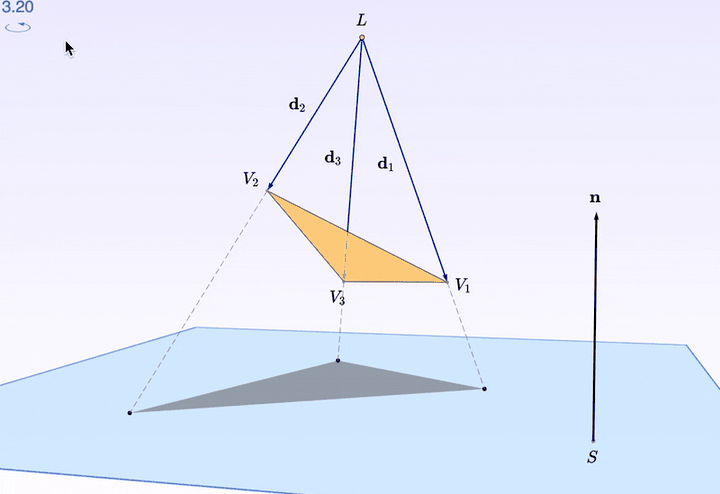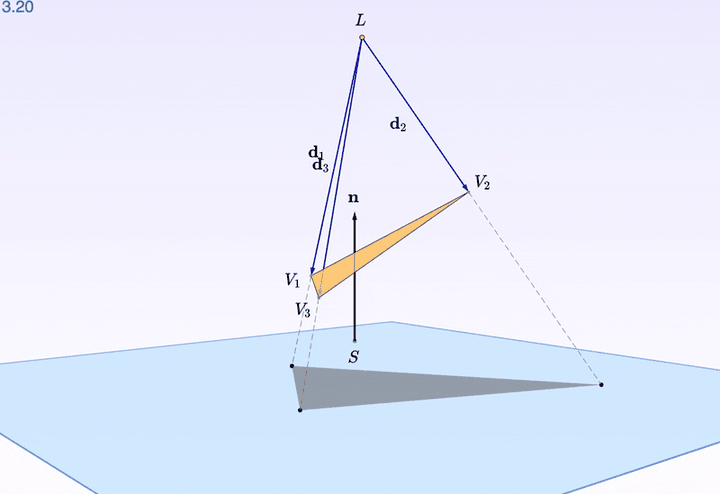
转起来还是不够立体?
三角形的每个 顶点 都可以拖拽。看上图,把一个顶点往上抬了抬,是不是漂亮了一些?
除此之外, 光源 的位置也可以调。
如果,你需要某个特殊的角度观察,比如由「桌面」出发的水平视角:
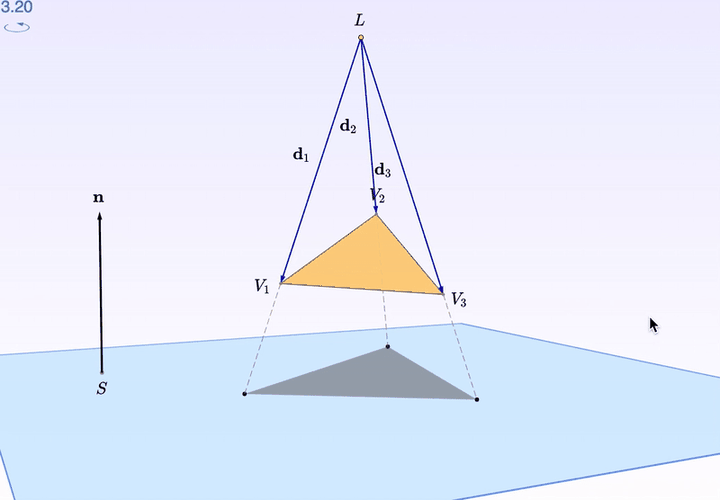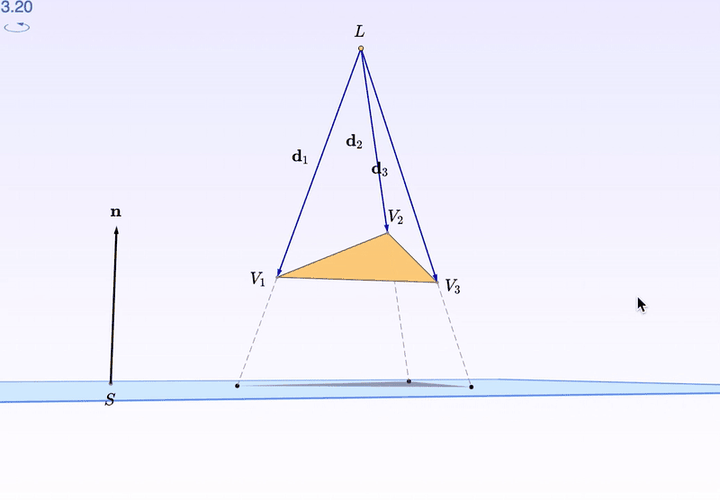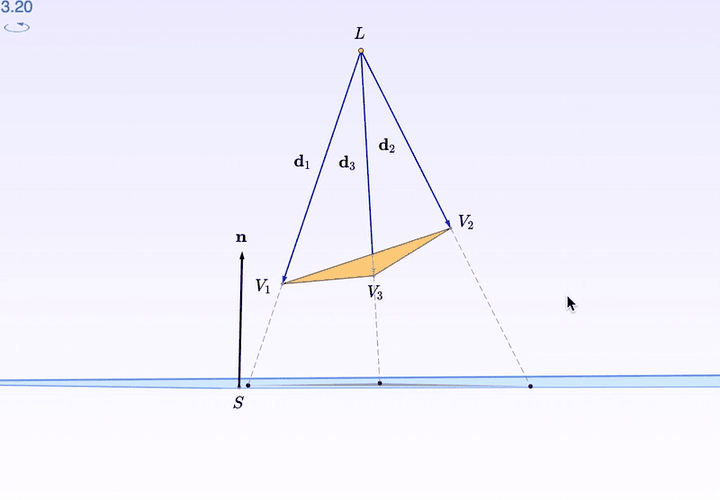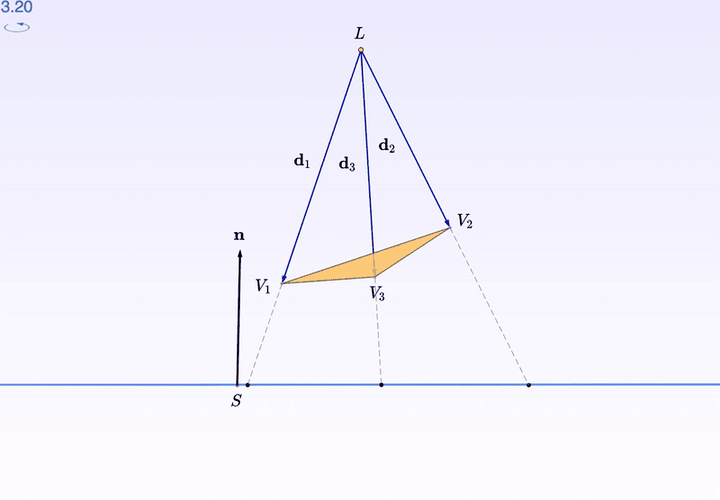
按住右键拖动,就可以调角度了。
调平了,再按左上角的旋转按钮感受一下:
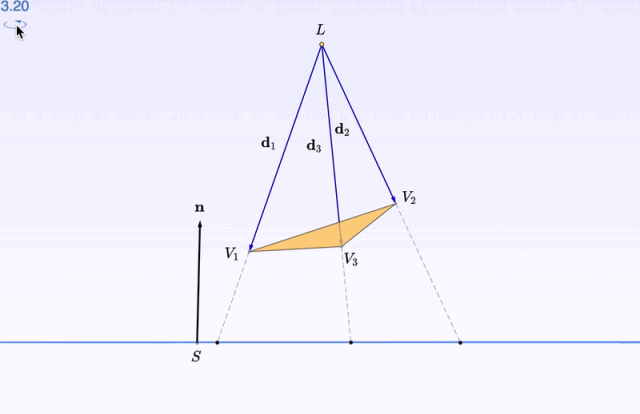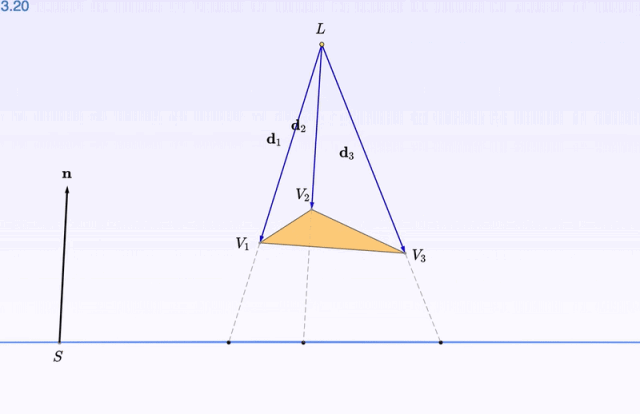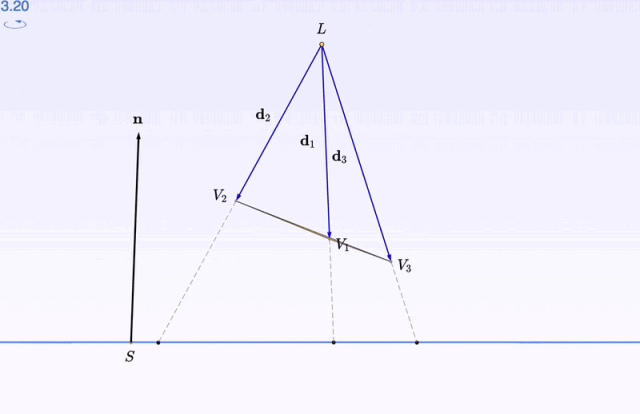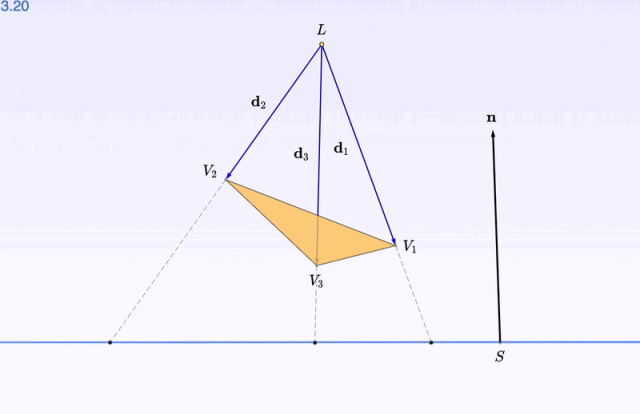
深度观察了图像之后,再开始 数学推导 的部分:比如影子的位置怎么算,大概就不会显得那么高高在上了。
另外,每当推导中用到了前面讲过的 定义 ,也不用翻回去查,只要把鼠标放在上面,定义就显示了:

已经完全没理由不好好学习了。
十一章
宏观了解一下章节分布吧,你会更有食欲的。
第一章:综述第二章:向量
第三章:点乘
第四章:叉乘
第五章:高斯消元法
第六章:矩阵
第七章:行列式
第八章:秩
第九章:线性映射
第十章:特征值和特征向量
第十一章:矩阵分解
作者团共有三人,J. Ström,K. Åström,以及T. Akenine-Möller。一人主攻数学,一人主攻图形学,一人主攻图像编码。
(可能是) 由于人少,从2013年写到现在,还有两章待续。有生之年系列。
祝福你,在第十章更新之前,学完第九章。
现在就可以开始看了:
— 完 —
量子位 · QbitAI
վ'ᴗ' ի 追踪AI技术和产品新动态
欢迎大家关注我们,以及订阅我们的知乎专栏











