谢邀, 这里从物体(刚体)的转动说起。
如果看得累,可以至少看完第一 、第二部分~
一、物体转动与力矩的关系
首先, 物体的运动有平动(Translational Motion)和转动(Rotational Motion) 。比如,在斜面上推动一滑块,则该滑块为平动;开门时门绕定轴转,则为该门为转动。
物体平动时有 位移 x ,转动时有 角位移 \theta ;平动时有 速度 v=\frac{dx}{dt} ,转动时有 角速度 \omega=\frac{d\theta}{dt} ;平动时有 加速度 a=\frac{dv}{dt}=\frac{d^{2}x}{dt^2} ,转动时有 角加速度 \alpha=\frac{d\omega}{dt}=\frac{d^2\theta}{dt^2} 。
力(Force)直接改变物体平动状态,力矩(Torque)直接改变物体的转动状态!
合外力是物体平动状态改变的原因,而合外力矩是物体转动状态改变的原因!
对于平动,有 F=ma ,其中 F 为合外力, m 为惯性质量(即质量), a 为加速度;而对于转动,有 M=J\alpha ,其中 M 为合外力矩, J 为转动惯量, \alpha 为角加速度。
(对于转动也有写法为 \tau=I\alpha ,其中 \tau 为合外力矩, I 为转动惯量, \alpha 为角加速度。)
由此可知, 力直接导致物体的加速度,而力矩直接导致物体的角加速度。 当然, 当合外力矩为0时,物体不转动 ,比如杠杆平衡。
二、对力矩计算的理解
力矩 是 力的一种使物体以一定角加速转动的能力。
M=r\times F (矢量的叉乘)
力矩的大小: M=r_{\bot}F=rF_{\bot}=rFsin\varphi
力矩的方向:垂直于 r 和 F 所在的平面
三、力矩与物体静平衡
一个物体静平衡,既需要达到平动上的平衡也需要达到转动上的平衡。
平动上的平衡要合外力为零,而转动上的平衡要合外力矩为零。
即静平衡需要: \Sigma F=0 且 \Sigma M=0
这里给一个简单的物体静平衡的例子:
一长度为 l 、质量为 m_1 的梯子倚靠在光滑墙面上,与地面夹角为 \theta 。某工人站在梯子的三分之二高处,其与手上器具的总质量为m_2 。 若墙面与梯子的摩擦忽略不计,为了防止梯子下滑,梯子与地面的静摩擦系数至少要是多少?
梯子不下滑,需要静平衡,则合力、合力矩都必须为0.
受力分析:
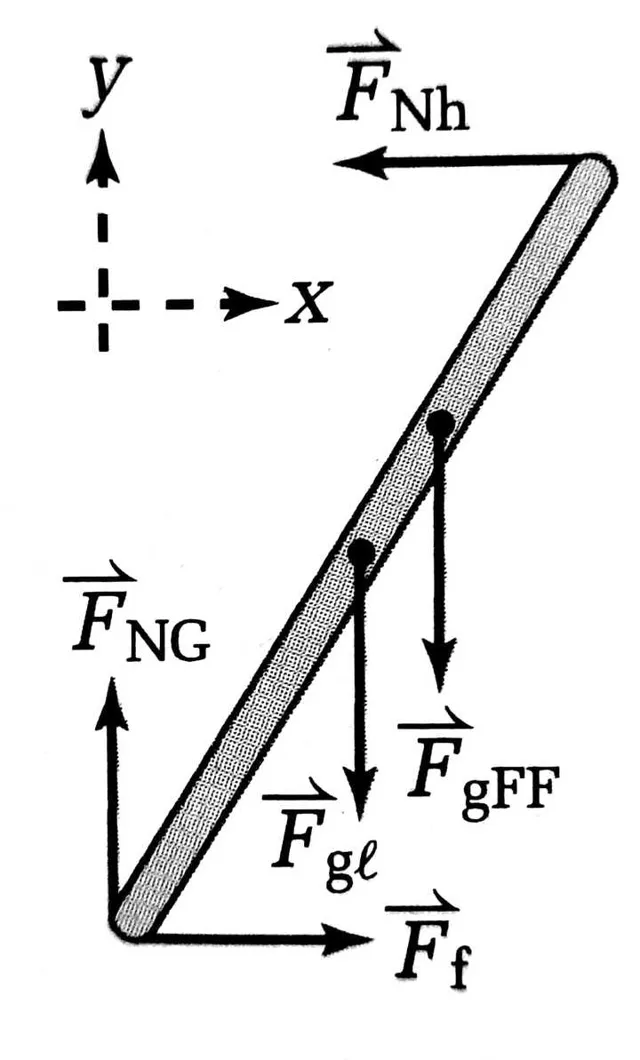
F_{Nh} - 墙对梯子的支持力
F_{NG} - 地面对梯子的支持力
F_{f} - 地面与梯子间的摩擦力
F_{gl} - 梯子的重力
F_{gFF} - 人与器具的总重力
选择梯子与地面的接触点为支点:
因为\Sigma F=0 ,所以 \Sigma F_x=0 且 \Sigma F_y=0 。
首先 \Sigma F_y=0
则 F_{NG}+F_{gl}+F_{gFF}=0
F_{NG}-m_1g-m_2g=0
F_{NG}=(m_1+m_2)g
同时 \Sigma M=0
则有 M_{NG}+M_{f}+M_{gl}+M_{FF}+M_{Nh}=0
0+0+\frac{l}{2}cos\theta m_1g+\frac{2}{3}lcos\theta m_2g+lsin\theta F_{Nh}=0
F_{Nh}=\frac{lcos\theta(\frac{1}{2}m_1g+\frac{2}{3}m_2g)}{lsin\theta} =cot\theta (\frac{1}{2}m_1g+\frac{2}{3}m_2g)
还有 \Sigma F_x=0
则 F_f+F_{Nh}=0
F_f=-F_{Nh}
\left| F_f\right|=\left| F_{Nh}\right|=cot\theta (\frac{1}{2}m_1g+\frac{2}{3}m_2g)
则梯子与地面的静摩擦系数至少为
\mu=\frac{F_f}{F_{NG}}=\frac{cot\theta (\frac{1}{2}m_1g+\frac{2}{3}m_2g)}{(m_1+m_2)g}=\frac{cot\theta (\frac{1}{2}m_1+\frac{2}{3}m_2)}{m_1+m_2}
四、力矩与物体平动加转动
一个物体平动遵守 F=ma , 转动遵守 M=J\alpha 。
【其中 F 为合外力, m 为惯性质量(即质量), a 为加速度; M 为合外力矩, J 为转动惯量, \alpha 为角加速度。】
这里给一个简单的物体平动+转动的的例子:
如图,细绳包裹着一个质量为 m ,半径为 R 的均匀实心圆柱体,圆柱体从静止开始下落。该圆柱的转动惯量为 \frac{1}{2}mR^2 。则当圆柱下落时细绳的拉力是多少?
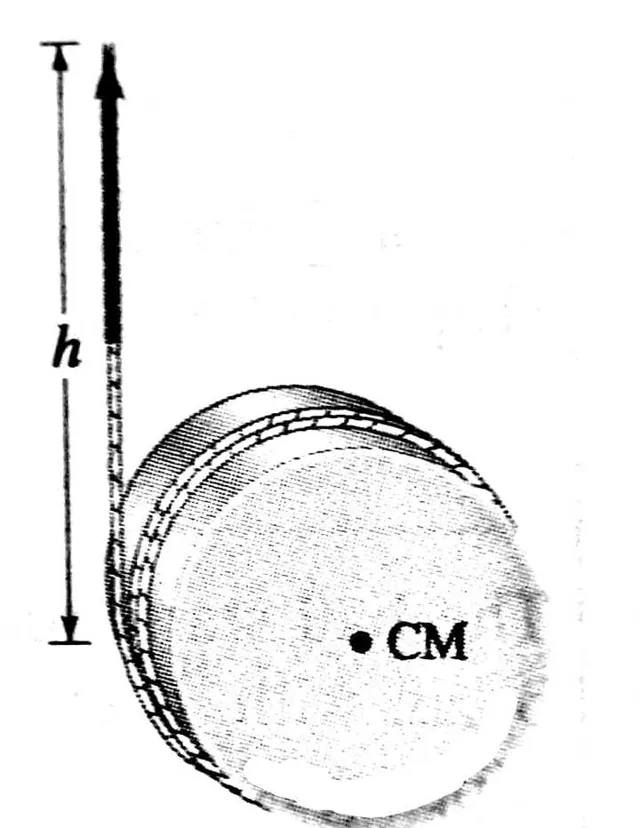
受力分析:
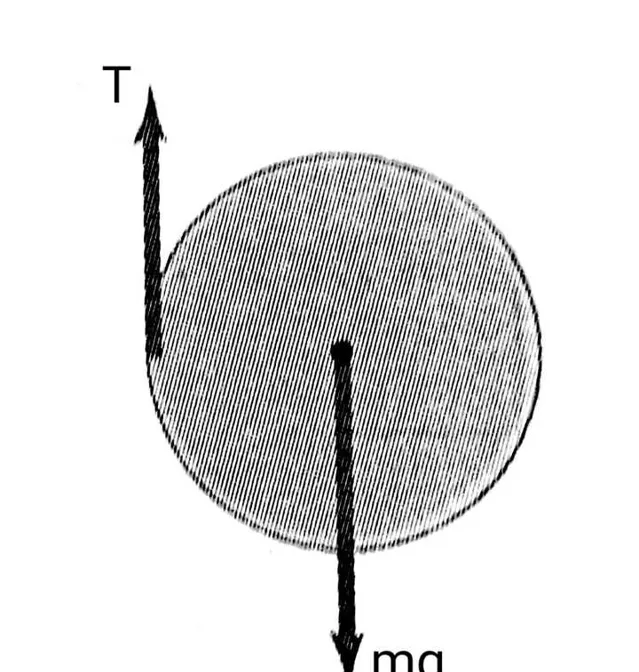
T - 细绳拉力
mg - 圆柱重力
该均匀圆柱绕质心转动,故力矩的大小为 M=TR 。
所以合外力矩为 M=TR 。
由于M=J\alpha
故有 TR=\frac{1}{2}mR^2\alpha ······ (1)
由于F=ma
故有 mg-T=ma ······ (2)
线加速度 a 与角加速度 \alpha 的关系为: a=R\alpha ······ (3)
联立(1)(2)(3),可得 a=\frac{2}{3}g
将a=\frac{2}{3}g 代入(1),得当圆柱下落时细绳的拉力为 T=\frac{1}{3}mg 。
五、力矩与角动量
物体的角动量等于其转动惯量与角速度的乘积: L=J\omega ,其中 L 为角动量, J 为转动惯量, \omega 为角速度。
则其微分形式为 dL=Jd\omega
由于 M=J\alpha , \alpha=\frac{d\omega}{dt}
故力矩可重新表示为 M=J\frac{d\omega}{dt}=\frac{dL}{dt}
由此可知, 物体所受的外力矩等于其角动量的变化率。
由M=\frac{dL}{dt} ,可得 \Delta L=\int_{t_1}^{t_2}Mdt
由此可知, 角动量的变化量是力矩对时间的累积效应。 \Delta L 也称为冲量矩。
这可以类比于物体平动所受的外力等于其动量的变化率、物体平动动量的变化量(冲量)是力对时间的累积效应。( F=\frac{dP}{dt} 、 \Delta P=\int_{t_1}^{t_2}Fdt )
六、力矩做功
首先,功的基本定义是:
dW=F\cdot dr
然后如下图:
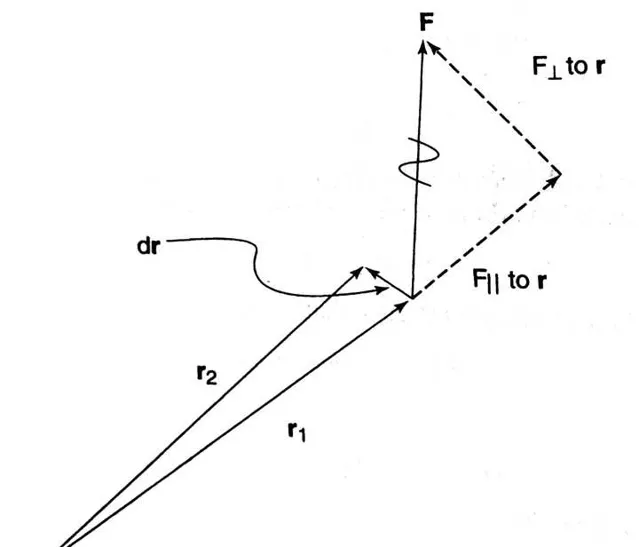
进一步地,根据矢量的点乘,对于定轴转动物体有 dW=F\cdot dr=(F_{\bot})(r d\varphi)
则 dW=(F_{\bot}r) d\varphi=Md\varphi
故 W=\int_{\varphi_1}^{\varphi_2}Md\varphi
因此, 对(定轴)转动物体做的功,是力矩做的功。
类比于物体平动时力做功 W=\int_{r_1}^{r_2}F\cdot dr ,物体转动时有力矩做功 W=\int_{\varphi_1}^{\varphi_2}Md\varphi 。
七、力矩与转动动能定理
之前所说外力矩做功有:W=\int_{\varphi_1}^{\varphi_2}Md\varphi
由于 M=J\alpha , \alpha=\frac{d\omega}{dt}
故有 W=\int_{\varphi_1}^{\varphi_2}J\alpha d\varphi=J\int_{\varphi_1}^{\varphi_2}\frac{d\omega}{dt}d\varphi
由于 \omega=\frac{d\varphi}{dt}
所以 W=J\int_{\omega_1}^{\omega_2}\omega d\omega=\frac{1}{2}J \omega_{2}^{2}-J\omega^2_1
因为 定义物体的转动动能为 E_k=\frac{1}{2}J\omega^2 , 所以 W=E_{k_2}-E_{k_1} 。
由此可知, 合外力矩对物体做的功等于该物体转动动能的变化量。这就是转动中的动能定理。
这可以类比于物体平动时的动能定理:合外力对物体做的功等于该物体平动动能的变化量。
八、机械能守恒时力矩与势能的关系
在没有非保守力时机械能守恒:
E_{总}=E_k+E_p=常数
其微分形式为
dE_{总}=0=dE_k+dE_p
由于功等于动能的变化量 W=\Delta E_k=E_k-E_{k_0} ,微分形式 dW=dE_k
所以当机械能守恒时势能与功的关系为
dW=dE_k=-dE_p
之前已提, 对于定轴转动物体有 dW=Md\varphi
则 M=\frac{dW}{d\varphi}
故有 M=-\frac{dE_p}{d\varphi}
(注意仅当力矩是由保守力产生时该关系才有效。)
九、力矩与功率的关系
功率的定义为 P=\frac{dW}{dt}
之前已提, 对于定轴转动物体有 dW=Md\varphi
则 P=\frac{dW}{dt}=\frac{Md\varphi}{dt}
由于角速度 \omega=\frac{d\varphi}{dt} ,所以有 P=M\omega
类比于物体平动时功率 P=F\cdot v ,物体转动时有功率 P=M\omega 。
不过其实我写的打的也挺累的,给个赞吧~











