好像还没人写解答,那我简单写一下我的解答,如果有误欢迎指出!
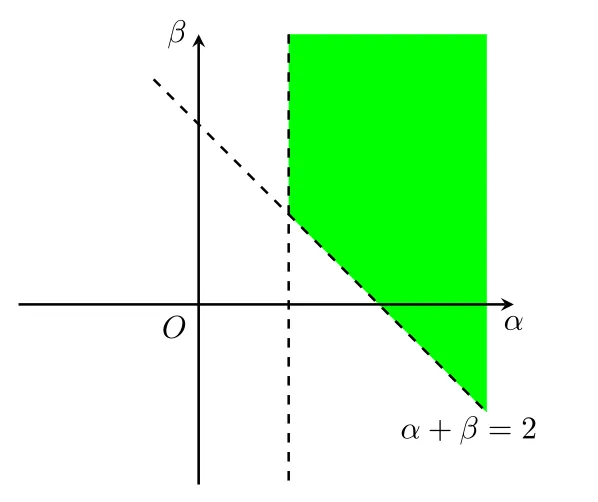
1. 求\alpha,\beta 使得级数\sum\limits_{n=1}^{\infty}\sum\limits_{m=1}^n\dfrac{1}{n^{\alpha}m^{\beta}} 收敛.解答: 当\alpha\le 1 时, 根据
\sum\limits_{m=1}^n\dfrac{1}{n^{\alpha}m^{\beta}} \ge \dfrac{1}{n^{\alpha}}, \\
于是原级数发散. 下设\alpha>1 .
(1)当\beta\ge 0 时, 由于
\int_{m}^{m+1}\dfrac{1}{x^{\beta}}\mathrm{d}x \le \dfrac{1}{m^{\beta}} \le \int_{m-1}^m\dfrac{1}{x^{\beta}}\mathrm{d}x, \\
所以
\int_1^{n}\dfrac{1}{x^{\beta}}\mathrm{d}x < \sum\limits_{m=1}^n\int_{m}^{m+1}\dfrac{1}{x^{\beta}}\mathrm{d}x \le \sum\limits_{m=1}^n\dfrac{1}{m^{\beta}} \le 1+ \sum\limits_{m=2}^n\int_{m-1}^m\dfrac{1}{x^{\beta}}\mathrm{d}x < 1+ \int_{1}^n\dfrac{1}{x^{\beta}}\mathrm{d}x,\\
(i)当\beta=1 时, 上式变成
\ln n < \sum\limits_{m=1}^n\dfrac{1}{m} < 1+\ln n, \qquad \Rightarrow \qquad \dfrac{\ln n}{n^{\alpha}} < \sum\limits_{m=1}^n\dfrac{1}{n^{\alpha}m} < \dfrac{1+\ln n}{n^{\alpha}}.\\
所以当\alpha>1 时, 原级数收敛; 当\alpha\le 1 时, 原级数发散.
(ii)当\beta\ne 1 时, 上式变成
\dfrac{1}{-\beta+1}(n^{-\beta+1}-1) \le \sum\limits_{m=1}^n\dfrac{1}{m^{\beta}} \le 1+\dfrac{1}{-\beta+1}(n^{-\beta+1}-1),\\
此时,
\dfrac{1}{-\beta+1}(n^{-\alpha-\beta+1}-n^{-\alpha}) \le \sum\limits_{m=1}^n\dfrac{1}{n^{\alpha}m^{\beta}} \le \dfrac{1}{n^{\alpha}}+\dfrac{1}{-\beta+1}(n^{-\alpha-\beta+1}-n^{-\alpha}).\\
当\alpha>1 且\alpha+\beta-1>1 (即\alpha+\beta>2 )时, 原级数收敛; 其余情况发散.
(2)当\beta < 0 时, 由于
\int_{m-1}^m\dfrac{1}{x^{\beta}}\mathrm{d}x < \dfrac{1}{m^{\beta}} < \int_{m}^{m+1}\dfrac{1}{x^{\beta}}\mathrm{d}x, \\
所以
1+\dfrac{1}{-\beta+1}(n^{-\beta+1}-1) = 1+ \int_{1}^n\dfrac{1}{x^{\beta}}\mathrm{d}x< \sum\limits_{m=1}^n\dfrac{1}{m^{\beta}} < \int_1^{n}\dfrac{1}{x^{\beta}}\mathrm{d}x = \dfrac{1}{-\beta+1}(n^{-\beta+1}-1),\\
此时,
\dfrac{1}{n^{\alpha}}+\dfrac{1}{-\beta+1}(n^{-\alpha-\beta+1}-n^{-\alpha})\le \sum\limits_{m=1}^n\dfrac{1}{n^{\alpha}m^{\beta}} \le \dfrac{1}{-\beta+1}(n^{-\alpha-\beta+1}-n^{-\alpha}) .\\
\alpha>1 且\alpha+\beta-1>1 (即\alpha+\beta>2 )时, 原级数收敛; 其余情况发散.
解答: 设椭圆C 上六个点为P_i(\cos\theta_i,\sin\theta_i) , i=1,2,3,4,5,6 , 并且0<\theta_i<\theta_{i+1} . 内接六边形P_1P_2P_3P_4P_5P_6 围成的区域记为\Omega . 为方便起见我们记\theta_7=\theta_1+2\pi , 那么P_7 就是P_1 .
(i)首先假设\Omega 包含原点, 此时\theta_{i+1}-\theta_i < \pi . 于是\Omega 的面积为
A(\Omega)=\dfrac{1}{2}\sum\limits_{i=1}^6\sin(\theta_{i+1}-\theta_i). \\
记\alpha_i=\theta_{i+1}-\theta_i , 则\alpha_1+\cdots+\alpha_6=\theta_7-\theta_1=2\pi , 由于\sin x 在(0,\pi) 上是凹函数, 所以根据Jensen不等式,
\dfrac{1}{6}\sum_{i=1}^6\sin\alpha_i \le \sin\left(\dfrac{1}{6}\sum_{i=1}^6\alpha_i\right)=\sin\dfrac{\pi}{3}=\dfrac{\sqrt{3}}{2}, \\
因此
A(\Omega)=\dfrac{1}{2}\sum_{i=1}^6\sin\alpha_i \le \dfrac{3\sqrt{3}}{2}. \\
等号成立条件是\alpha_1=\cdots=\alpha_6=\dfrac{\pi}{3} , 此时\Omega 是边长为1的正六边形.
(ii)若\Omega 不包含原点, 则圆C 内部有一半与\Omega 不相交, 于是A(\Omega) < \dfrac{\pi}{2} < \dfrac{3\sqrt{3}}{2} .
综上, A(\Omega) 的最大值为\dfrac{3\sqrt{3}}{2} .
(2)对于一般的情况, 对单位圆x^2+y^2=1 沿着两个坐标轴作伸缩变换即可得到椭圆C , 此时面积的最大值也会有相应的伸缩变换, 故A(\Omega) 的最大值为\dfrac{3\sqrt{3}ab}{2} .
3. 设G 按加法构成群, 满足G=\langle a,b\rangle , 其中a,b 为生成元, 且12a+5b=0 , 24a+16b=0 .(1)求a 的阶的所有可能值.
(2)求群G 在同构意义下的群结构.
解: 由条件, G 的所有元素形如\{ma+nb|m,n\in\mathbb{Z}\} , 其中a,b\ne 0 .
(1)由条件, 24a+10b=2(12a+5b)=0 且24a+16b=0 , 因此6b=0 , 从而b 可能是2,3,6阶的.
再由12a+5b=0 可得12a-b=0 并且72a+30b=0 , 所以72a=0 . 所以a 可能是2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72阶的. 但12a=b\ne 0 , 所以a 不可能是2,3,4,6,12阶的, 于是只可能是8,9,18,24,36,72阶.
(i)若b 是2阶的, 则由24a+16b=0 可得24a=0 , 所以a 只可能是8,24阶的.
①当G=\mathbb{Z}/8\mathbb{Z} , b=4 , a=1 时, 满足12a+5b=32=0 且24a+16b=0 .
②当G=\mathbb{Z}/24\mathbb{Z} , b=12 , a=1 时, 满足12a+5b=72=0 且24a+16b=24+192=0 .
(ii)若b 是3阶的, 则由12a-b=0 可得36a-3b=0 , 故36a=0 , 所以a 只可能是9,18,36阶的.
①当G=\mathbb{Z}/9\mathbb{Z} , b=3 , a=1 时, 满足12a+5b=27=0 且24a+16b=72=0 .
②当G=\mathbb{Z}/18\mathbb{Z} , b=6 , a=5 时, 满足12a+5b=90=0 且24a+16b=120+96=216=0 .
③当G=\mathbb{Z}/36\mathbb{Z} , b=12 , a=1 时, 满足12a+5b=72=0 且24a+16b=24+192=216=0 .
(iii)若b 是6阶的, 则a 只可能是8,9,18,24,36,72阶的.
当G=\mathbb{Z}/72\mathbb{Z} , b=12 , a=1 时, 满足12a+5b=72=0 且24a+16b=24+192=216=0 .
综上所述, a 的阶的所有可能值是8,9,18,24,36,72.
(2)G 中任意元素可以表示为ma+nb=ma+12na=(m+12n)a , 其中m,n\in\mathbb{Z} , 而m+12n 可以表示任意整数, 所以G=\langle a\rangle . 由(1), a 只可能是8,9,18,24,36,72阶, 所以根据循环群的定义, G 在同构意义下只可能是8,9,18,24,36,72阶循环群, 即G 只可能与\mathbb{Z}/k\mathbb{Z}(k=8,9,18,24,36,72) 同构.
4. 在三维空间V 中, 5个两两不同的二维空间两两相交为一维空间, 求交出的一维空间的个数的可能值.(一定有更方便的做法)
结论1: 若三个二维空间相交得到的一维子空间有两个相同, 则三个一维子空间都相同, 即e_{ij}=e_{ik} 能推出e_{ij}=e_{ik}=e_{jk} .结论1证明: 设三个二维空间为V_i,V_j,V_k . 若e_{ij},e_{jk},e_{ik} 有其中两个相同, 例如e_{ij}=e_{ik} , 则(V_i\cap V_j)\cup (V_i\cap V_k)=V_i\cup(V_j\cap V_k)=e_{ij}\supset e_{jk} , 所以必有e_{jk}=e_{ij} . \square
结论2: 若四个二维空间V_i,V_j,V_k,V_l 中, V_i 与V_j 相交的一维子空间等于V_k 与V_l 相交的一维子空间, 则这四个二维子空间交出来的一维子空间都相同, 即e_{ij}=e_{kl} 能推出e_{ij}=e_{jk}=e_{ik}=e_{il}=e_{jl}=e_{kl} .结论2证明: 设四个二维空间为V_i,V_j,V_k,V_l , 由条件, e_{ij}=V_i\cap V_j=V_k\cap V_l=e_{kl} , 但是
\begin{aligned} &\quad (V_j\cap V_k)\cup (V_i\cap V_k)\cup (V_j\cap V_l)\cup (V_i\cap V_l) \\ &=(V_k\cap(V_i\cup V_j)) \cup (V_l\cap(V_i\cup V_j)) \\ &=(V_i\cup V_j)\cap (V_k\cup V_l) = e_{ij}, \end{aligned}\\
所以e_{jk},e_{ik},e_{jl},e_{il}\subset e_{ij} , 从而必有e_{ij}=e_{jk}=e_{ik}=e_{il}=e_{jl}=e_{kl} . \square
证明: 假设二维空间为V_1,V_2,V_3,V_4,V_5 , 并且记V_i\cap V_j=e_{ij} 是V 的一维子空间. 设S 为交出的一维空间的个数.
首先, V_1,V_2,V_3 之间交出的一维子空间: V_1\cap V_2=e_{12} , V_1\cap V_3=e_{13} , V_2\cap V_3=e_{23} .
(1)若e_{12},e_{13},e_{23} 有其中两个相同, 由结论1可知e_{12}=e_{13}=e_{23} . 下面考虑e_{14},e_{24},e_{34} .
①若e_{14},e_{24},e_{34} 至少有一个等于e_{12}=e_{13}=e_{23} , 例如e_{14}=e_{12}=e_{13}=e_{23} , 则根据结论1, e_{24}=e_{14}=e_{12} , 并且e_{34}=e_{14}=e_{13} . 于是这六个一维子空间都相同.
(a)若e_{15},e_{25},e_{35},e_{45} 至少有一个等于e_{12}=e_{13}=e_{23}=e_{14}=e_{24}=e_{34} , 例如e_{15} 等于上述六个一维子空间, 则根据结论1, e_{25}=e_{15}=e_{12} , e_{35}=e_{15}=e_{13} , e_{45}=e_{15}=e_{14} . 所以十个一维子空间都相同, 从而\boxed{S=1} .
(b)若e_{15},e_{25},e_{35},e_{45} 都不等于e_{12}=e_{13}=e_{23}=e_{14}=e_{24}=e_{34} , 那么e_{15},e_{25},e_{35},e_{45} 也两两不同(不然与结论1矛盾), 从而\boxed{S=5} .
②若e_{14},e_{24},e_{34} 都不等于e_{12}=e_{13}=e_{23} , 则e_{14},e_{24},e_{34} 两两不同(不然与结论1矛盾),
(2)若e_{12},e_{13},e_{23} 两两不同,
①若e_{14},e_{24},e_{34} 有两个相同(不可能三个相同, 与结论1矛盾), 不妨设e_{14}=e_{24}=e_{12} (结论1).
②若e_{14},e_{24},e_{34} 也两两不同并且不等于e_{12},e_{13},e_{23} (不然与结论1矛盾).
综上, 所有不同的一维子空间个数的可能值为1,5,6,8,10.
5. 在平面直角坐标系中,(1)三个整点组成的三角形的面积最小值为多少?
(2)圆心在原点、半径为R 的圆上一段长为R^{\frac{1}{3}} 的圆弧上三点的面积最大为多少?
(3)在(2)中这段圆弧上至多有几个整点?
(1)不妨设其中一个点是原点, 另外两个点为(a_1,b_1) 与(a_2,b_2) . 则面积为
\dfrac{1}{2}\left|\det\begin{bmatrix}a_1 & b_1 \\ a_2 & b_2\end{bmatrix}\right|=\dfrac{1}{2}|a_2b_1-a_1b_2|. \\
由于a_1,b_1,a_2,b_2 都是整数, 所以|a_2b_1-a_1b_2|\ge 1 , 等号成立的一个条件是a_1=1,b_1=0,a_2=0,b_2=1 , 此时三角形面积为\dfrac{1}{2} . 所以三个整点组成的三角形的面积最小值为\dfrac{1}{2} .
(2)设长为R^{\frac{1}{3}} 的圆弧的圆心角为\theta , 则
2\pi R\dfrac{\theta}{2\pi}=R^{\frac{1}{3}}, \\
故\theta=R^{-\frac{2}{3}}.
①当\theta \ge \dfrac{4\pi}{3} 即R\le\left(\dfrac{3}{4\pi}\right)^{\frac{3}{2}} 时, 面积最大值为\dfrac{3\sqrt{3}}{4}R^2 , 此时三个顶点构成等边三角形.
②当\theta < \dfrac{4\pi}{3} 即R>\left(\dfrac{3}{4\pi}\right)^{\frac{3}{2}} 时, 面积最大值在两个顶点为圆弧端点、一个顶点为圆弧中点取到, 此时面积的最大值为
\begin{aligned} A&=\dfrac{1}{2}R^2\left[\sin\dfrac{\theta}{2}+\sin\dfrac{\theta}{2}-\sin\theta\right] \\ &=\dfrac{1}{2}R^2\left[2\sin\dfrac{R^{-\frac{2}{3}}}{2}-\sin(R^{-\frac{2}{3}})\right]. \end{aligned}\\
(3)由于R>0 , 所以根据不等式x-\dfrac{x^3}{6}\le \sin x\le x(x\ge 0) , 可知
A \le \dfrac{1}{2}R^2\left[R^{-\frac{2}{3}} - \left(R^{-\frac{2}{3}}-\dfrac{R^{-2}}{6}\right)\right] =\dfrac{1}{12} < \dfrac{1}{2},\\
所以根据(1)可知这段圆弧上不可能有3个整点.
下面构造有2个整点的例子: 考虑圆心为(0,0) , 且经过(1,y_0) 和(-1,y_0) 的圆, 则半径R=\sqrt{1+y_0^2} . 过两点(1,y_0) 和(-1,y_0) 的圆弧的圆心角为\alpha=2\arctan\dfrac{1}{y_0} , 弧长可以写成y_0 的函数:
l(y_0)=\alpha R=2R\arctan\dfrac{1}{y_0}=2\sqrt{1+y_0^2}\arctan\dfrac{1}{y_0}. \\
所以\lim\limits_{y_0\to+\infty}l(y_0)=2 . 取y_0 充分大使得
l(y_0)=\alpha R<\theta=R^{\frac{1}{3}}, \\
于是此时在弧长为R^{\frac{1}{3}} 的圆弧上存在两个整点.
6. n 阶矩阵的所有元素均为\pm 1 , 求所有此类矩阵的行列式的平均值.解: 假设A 是一个n 阶矩阵, 定义\tilde{A} 为把A 的第一行的1 换成-1 、-1 换成1 得到的n 阶矩阵, 相当于把A 的第一行全都取相反数. 则根据行列式的运算法则, \det(\tilde{A})=-\det A , 即\det(\tilde{A})+\det A=0 .
下面固定n 阶矩阵的第2\sim n 行. 由于第1行有2^n 种不同的情况, 所以一共有2^n 个不同的矩阵, 把这些矩阵的全体记为\mathscr{A} . 对任意的A\in\mathscr{A} , 都有\tilde{A}\in\mathscr{A} 且满足\det(\tilde{A})+\det A=0 . 所以\mathscr{A} 中所有矩阵的行列式之和为0 , 并且跟2\sim n 行的元素选取无关.
因此, 此类矩阵的行列式之和都为0 , 平均值也为0 .











