摘要
近年来,氪金抽卡逐渐演变成为游戏中相对主流的新型付费模式。一方面,抽卡的以小博大能拉低用户的付费门槛,且能潜移默化地完成直购付费难以做到的捆绑销售;另一方面,若抽卡的随机性不加以控制,也会给相当部分用户带来十分糟糕的体验。
首先,本文从抽奖系统的随机性设计作为切入点,采用统计学方法分析了完全随机、直接保底、PRD保底的数据分布规律,得出「可控性大小依次为PRD保底>直接保底>完全随机」的结论。
然后,本文依次介绍了在感官体验上具有天然优势的双层抽奖模型,绑定商店系统的抽奖积分模型,并且罗列了一些常见动态奖池的数值推导方法。
最后,本文推广到广义上的随机性设计,抽象出可控性随机的三大指标:随机幅度、随机频次和概率分布,并围绕这三大指标列举了一些应用实例。
关键词: 奖池;保底;随机性;可控性
一、 引言
在大多数游戏中,抽奖是不可或缺的重要玩法,也是促进玩家消费的主要手段。比起抽奖,虽然直购活动的性价比更高,但是玩家更倾向于选择能够「以小博大」的抽奖活动。本文将从数值角度由浅及深地介绍抽奖系统的模型设计,并着重结合【明日方舟】和【原神】进行数据分析。
个人思路:1)先吃透简化的基础数值模型,后研究复杂的进阶数值模型;
2)性价比是影响玩家经济决策的主要因素,但不是绝对的;
3)数值设定的切入点是找到直接影响玩家游戏体验的统计变量。
二、 最简抽奖模型
2.1 数值模型
现有一个静态奖池,每次抽奖均为独立且相同的随机事件,每次抽奖的消耗为C,奖品i的中奖几率为Pi,价值为Vi,i=1,2,...,N。
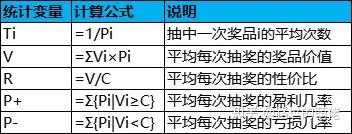
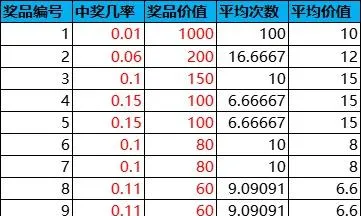
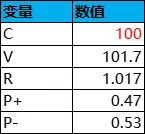
举个例子,设有一个抽奖活动,共有10种奖品,每次抽奖的消耗为100,每种奖品的中奖几率和价值如下,则根据公式即可计算出每种奖品中奖的平均次数Ti、平均奖品价值V、性价比R、平均每次抽奖的盈利几率P+、亏损几率P-,如下表所示:
2.2 存在问题
1)概率权重(程序)
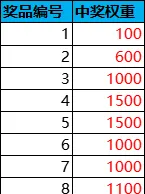
在游戏中,抽奖活动是会随时更新的,比如新增一种奖品。若数据配置表直接配置中奖几率,则每次新增奖品时,每种奖品的中奖几率都要重新调整,导致更新维护相对繁琐。因此,数据配置表一般不是直接配置中奖几率,而是配置成中奖权重。中奖权重Wi和中奖几率Pi的换算关系为Pi=Wi/ΣWj。
上述例子中,每种奖品的中奖权重如下表所示:(填法不唯一,总权重一般控制在10000左右,确保可调空间足够大)
2)连续中大奖或连续不中大奖的极端情况
玩家参加抽奖活动往往抱着「以小博大」的心理,也就是说,大奖才是玩家的核心关注点。具体而言,实际抽多少次才能抽中大奖,这是玩家参与抽奖活动的核心体验。
设抽中大奖几率为P*,抽中大奖的平均次数为T*,抽中大奖的实际次数为T。显然,T*=1/P*,这也是玩家预期抽中大奖次数的参考数值。然而,T*要在大数据支撑下才具有实际意义。玩家抽中大奖的实际次数T和平均次数T*是截然不同的,T<<T*或者T>>T*的两种极端情况在游戏中时有发生。

上述例子中,奖品1为大奖,中奖几率P*=0.01,抽中大奖的平均次数T*=1/P*=100,下面给出几种情况的计算结果:
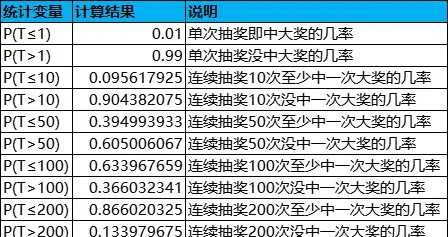
为了更加直观,把上述情况划分成互不相交的几种情况,计算结果如下表所示:
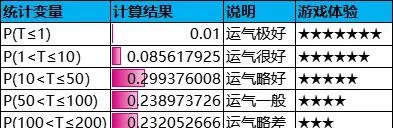
由此可见,即使抽中大奖的平均次数为100,依旧有高达36.6%的几率超过100次才能抽中大奖,甚至出现1.8%的几率超过400次才能抽中大奖;与之相对,也会出现1%的几率单抽即中大奖。
设参与抽奖活动的玩家人数为10000,每个玩家直到抽中一次大奖即停止抽奖,每次抽奖的所需付费金额为1元。根据上述抽奖次数的概率分布,即可计算出各抽奖区间的抽奖次数中位值、玩家人数分布和付费金额分布。
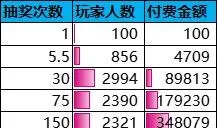
从付费金额的分布来看,超过50%的付费来源于「运气略差」和「运气很差」这两大群体。也就是说,核心付费群体的运气偏差,抽奖体验不好。另一方面,运气不差的玩家人数为3950≈40%,付费金额仅为94622≈9%。这种情况跟前面的核心付费群体恰好形成一种对立反常现象。从长远来看,这将会导致核心付费群体的逐渐流失,玩家付费习惯趋于小额化,不利于游戏的可持续发展。
为了杜绝这些极端异常现象,如今市面上很多游戏的抽奖活动中针对大奖都会加入保底机制,其中卡牌类游戏尤为明显。
2.3 实际应用
1)价值相当的奖励组
比如随机部位装备掉落、随机属性宝石宝箱、随机同星级角色等等。若奖励组中同时包含稀有道具和普通道具,则可将稀有道具进行碎片化处理,并改为投放稀有道具碎片。
2)高频次随机事件
比如挂机打怪、野外采集、伤害波动等等。
3)非小概率事件
比如低级装备掉落、普通材料掉落、游戏币掉落等等。
三、 保底机制
3.1 直接保底
设A为最小保底次数,B为最大保底次数,0≤A<B,则直接保底的大奖概率分布如下:

记直接保底模型为DR-GT(A, B, P*)。
根据概率论知识,抽中大奖的平均次数T*的计算公式如下:
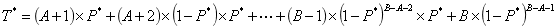
根据代数知识,化简可得:
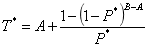
举个例子,对于直接保底模型DR-GT(10, 200, 0.01),代入公式可得:
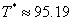
下面直接给出此保底规则下的抽奖次数的概率分布和付费金额的数据表和曲线图:
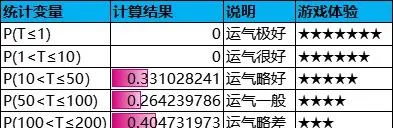
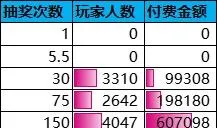


对照之前的例子,最显著的差异就是「T≤10」和「T>200」的两种极端情况直接被剔除。虽然根绝了抽奖的两种极端情况,但是由于直接保底的设计过于粗糙,从而带来一些新的问题。其一是保底规律太明显,随机性降低,抽奖体验趋于平庸;其二是概率分布不平滑,依然有较大概率吃保底。在本例中,P(T=200)=(1-0.01)^(200-10-1)≈14.96%,即吃保底的几率为14.96%,从而导致吃保底玩家的总付费金额达到300000≈31%。也就是说,核心付费群体的抽奖体验依旧是偏差的。
3.2 PRD保底
设大奖基础概率为P*,基础概率次数为A,最大保底次数为B,大奖概率增量为ΔP,1≤A<B,则PRD保底的大奖概率分布如下:

记PRD保底模型为PRD-GT(A, B, P*, ΔP)。其中,最大保底次数B=min{T|P*+(T-A)×ΔP≥1}。
根据概率论知识,抽中大奖的平均次数T*的计算公式如下:
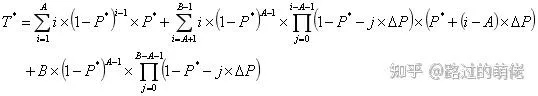
举个例子,对于PRD保底模型PRD-GT(100, 199, 0.01, 0.01),代入公式(Excel拉表)可得:
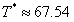
下面直接给出此保底规则下的抽奖次数的概率分布和付费金额的数据表和曲线图:
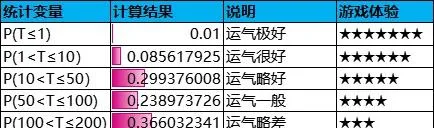
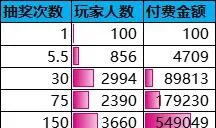
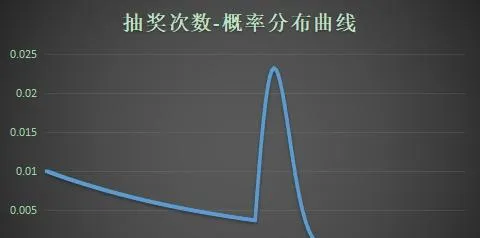
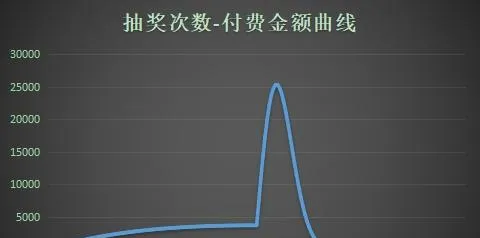
从抽奖次数-概率分布曲线来看,P(T≥130)≈0,即抽中大奖的实际次数几乎不超过130次,也就几乎更不可能吃保底了。相较于直接保底,PRD保底规律不太明显,具有一定的随机性,抽奖体验良好。基于这些优点,PRD保底逐渐成为相对主流的抽奖保底规则。
3.3 模拟抽奖
下面我们模拟无保底、直接保底和PRD保底的抽奖情况,并根据样本统计数据来比较它们之间的差异性。
1)无保底:p*=1/50=0.02
2)直接保底:DR-GT(0, 100, 0.016)
3)PRD保底:PRD-GT(57, 156, 0.01, 0.01)
上述三个抽奖模型都是建立在大奖平均次数T*≈50的前提下,其中,直接保底和PRD保底的数值模型并不唯一。下面是用VBA模拟(详见 第八章的VBA代码附录 )三种情况200次大奖的抽奖次数分布样本,并计算出相应的样本统计量。

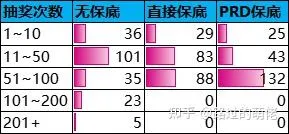
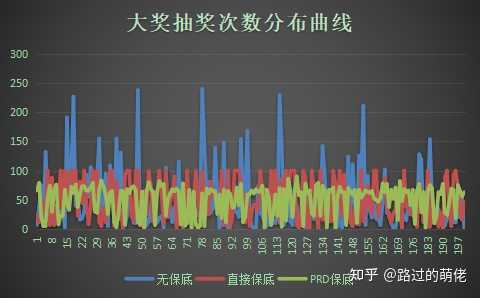
从最小次数来看,由于基础概率为0.01~0.02,样本总数为200,三种抽奖模型都出现了一次即中大奖(或连续两次中大奖)的正常现象;从最大次数来看,无保底的可控性最差,PRD保底的可控性最好,尽管PRD保底的保底次数大于直接保底的最大保底;从平均次数来看,三种抽奖模型都为50左右,原因是三个模型都是建立在T*≈50的基础上;从极差和标准偏差来看,无保底的数据分布最为混乱,PRD的数据分布最为均匀,这一点从分布曲线图可以明显地看出来。
3.4 实际应用
1)直接保底的次级奖励组
比如【明日方舟】的「10次内寻访必得5★以上干员」为直接保底模型DR-GT(0, 10, 0.08)。
2)PRD保底的次级奖励组
比如【原神】的角色池4星保底为PRD保底模型PRD-GT(8, 10, 0.051, 0.51),武器池4星保底为PRD保底模型PRD-GT(7, 9, 0.06, 0.6)。
3)PRD保底的顶级奖励组
比如【原神】的角色池5星保底为PRD保底模型PRD-GT(73, 90, 0.006, 0.06),武器池5星保底为PRD保底模型PRD-GT(62, 77, 0.007, 0.07),【明日方舟】的6星保底为PRD保底模型PRD-GT(50, 99, 0.02, 0.02)。
[数据讨论] 原神抽卡概率工具表 - 更新n命m精所需抽数/常驻五星类别预测 NGA玩家社区
4)直接保底的up大保底
比如【原神】的角色up池大保底为直接保底模型DR-GT(0, 2, 0.5),武器up池定轨机制为直接保底模型DR-GT(0, 3, 0.375)。这里说明一下,【原神】抽卡为双层抽奖模型,第1层决定获得奖励的星级,第2层决定该星级下的具体奖励。大保底和定轨机制是指第2层的up奖励。
四、 双层抽奖模型
4.1 数值模型
现有一个静态奖池,奖池分为两层,每次抽奖的消耗为C,第1层的第i个奖励组的中奖几率为Pi,在抽中第i个奖励组的前提下,第2层的第j个奖品的中奖几率为Pij,价值为Vij,i=1,2,...,N,j=1,2,...,Ni。
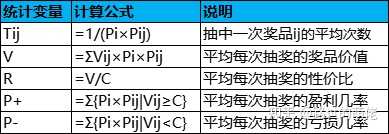
举个例子,设有一个抽奖活动,共有3个奖励组(2+3+5),每次抽奖的消耗为100,奖励的概率和价值如下,则根据公式即可计算出每种奖品中奖的平均次数Tij、平均奖品价值V、性价比R、平均每次抽奖的盈利几率P+、亏损几率P-,如下表所示:
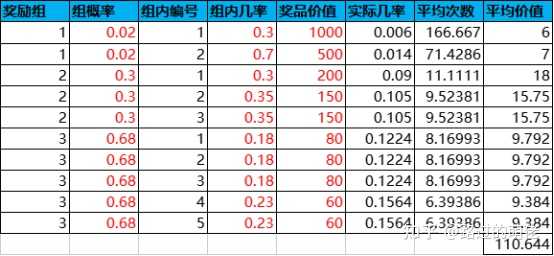
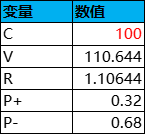
双层抽奖模型可转换为最简抽奖模型;反之,通过对奖品进行分组,最简抽奖模型也可转换为双层抽奖模型。若只看抽奖结果,则双层抽奖模型近乎等效于最简抽奖模型。实际上,双层抽奖模型的意义主要体现于过程而非结果。
4.2 模型优点
1)可赋予双重抽奖体验
在逻辑上,双层抽奖模型可分为两个阶段。第1阶段决定哪个奖励组,而第2阶段决定该奖励组下的哪个奖品。在程序上,一次抽奖过程几乎是瞬间完成的;在表现上,一次抽奖过程分为抽奖动画/特效和奖品展示。显然,抽奖动画赋予了第1阶段的抽奖体验,而奖品展示赋予了第2阶段的抽奖体验。若游戏直接给出抽奖结果,则抽奖体验将会大打折扣。
【明日方舟】的单次抽卡过程为:互动拉链(前1/10进度的表现是一样的,拉开1/10后根据不同星级显示不同颜色闪光特效)→闪光特效(白/紫/金/彩光对应3/4/5/6星)→卡牌展示(白/灰/金/彩边对应3/4/5/6星)→星级展示(3/4/5/6星)→干员展示→奖励结算;十连抽卡过程为:互动拉链(同上)→闪光特效(根据最高星级)→卡牌展示(10个卡牌的星级)→卡牌1星级展示→卡牌1干员展示→卡牌2星级展示→卡牌2干员展示→...→卡牌10星级展示→卡牌10干员展示→奖励结算。
【原神】的单次抽卡过程为:流星坠落(0-2秒的表现是一样的,2-6秒根据不同星级显示不同颜色闪光特效)→闪光特效(蓝/紫/金光对应3/4/5星)→角色/武器展示→奖励结算;十连抽卡过程为:流星坠落(同上)→闪光特效(根据最高星级)→角色/武器1展示→角色/武器2展示→...→角色/武器10展示→奖励结算。
对比【明日方舟】和【原神】的抽卡过程,前者更为复杂,多了两个小阶段,分别是「卡牌展示」和「星级展示」。对于单抽,这两个小阶段所表现的信息跟闪光特效是一样的,可以说是冗余的;对于十连抽,不同于闪光特效只表现最高星级信息,卡牌展示表现了10个卡牌的星级信息,星级展示则逐个表现每个卡牌的星级信息。基于这一差异,【明日方舟】和【原神】的十连抽卡体验是有区别的,特别是抽到2个以上大奖时的信息反馈。
在不跳过抽奖动画的前提下,某玩家在【明日方舟】某次十连抽出3个6星,得到的反馈是「卧槽!出6星了!」→「卧槽!!!竟然出3个6星!」;而在【原神】某次十连抽出3个5星,得到的反馈是「卧槽!出5星了!」→「卧槽!!又一个5星!」→「卧槽!!!又来一个5星!」。 在这种情况下,【明日方舟】的抽奖反馈是爆发式的,【原神】的抽奖反馈是递进式的。造就这一体验差异的根本原因是【明日方舟】的「卡牌展示」阶段提前表现10个卡牌的星级信息。抽奖动画的设计灵感也能在现实生活中找到影子。 以双色球为例,游戏的抽奖动画就对应双色球的开奖过程,这一过程无疑延长了抽奖体验。

2)直观且精细的抽奖概率
一方面,奖励组的划分直观地体现了组内奖品稀有度的性质,奖励组的几率直观地体现了组内奖品的获取难度。另一方面,若单层抽奖概率的精度为r,则双层抽奖概率的精度为r^2。
五、 抽奖积分
5.1 数值模型
设每次抽奖返还F点积分,积分可用于兑换抽奖券或其它资源(兑换抽奖券的性价比≥其它资源),抽奖券的兑换价格为G点积分,平均抽奖k次即可兑换一张抽奖券,即G=k×F。每次抽奖消耗为C,而每张抽奖券为G点积分,以此作为积分的价值标准,则每点积分的价值为C/G。于是,兑换抽奖券的性价比为C/(G×C/G)=1。
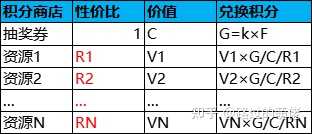
在此模型中,F、k、Ri为设定值,C、Vi为已知值,而商品的兑换积分为导出值。其中,F是可随意取的,在尽量小的前提下保证其它推导结果均为整数即可;k取为10左右;Ri则根据具体项目需求自行设定。 为了避免玩家消费的单一化,积分商店的商品会设置每期的购买数量上限,并针对不同档次的付费玩家,设置不同档次的商品。 比如,1档商品的性价比约为2,限购数量较少,零氪党恰好搬空1档商品;2档商品的性价比约为1,限购数量较多,中氪党可恰好搬空1档商品+2档商品;3档商品的性价比约为0.5,无限购上限,用于消耗重氪党溢出的剩余积分。
5.2 积分拆解
每次抽奖结果大致可分为两种情况,即抽到稀有奖励或抽到普通奖励。若抽到稀有奖励,则本次抽奖返还F1点稀有积分;若抽到普通奖励,则本次抽奖返还F2点普通积分。记抽到稀有奖励的概率为P*,则抽到普通奖励的概率为1-P*,平均每次抽奖返还稀有积分为F1×P*,返还普通积分为F2×(1-P*)。每张抽奖券的兑换价格为G1点稀有积分或G2点普通积分,集齐G1点稀有积分的平均抽奖次数为k1=G1/F1/P*,集齐G2点普通积分的平均抽奖次数为k2=G2/F2/(1-P*),兑换一张抽奖券的综合平均抽奖次数为k=(k1×k2)/(k1+k2)。以抽奖券的兑换价格作为积分的价值标准,可得每点稀有积分的价值为C/G1,每点普通积分的价值为C/G2。
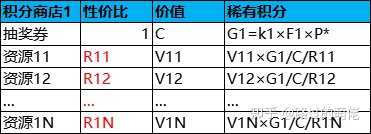
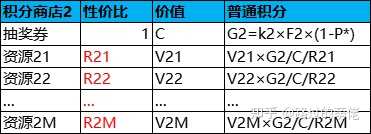
在此模型中,F1、F2、k1、k2、R1i、R2i为设定值,C、P*、V1i、V2i为已知值,而商品的兑换积分为导出值。其中,F1、F2是可随意取的,在尽量小的前提下保证其它推导结果均为整数即可;k1、k2取为10左右,且保证k也为10左右;R1i、R2i则根据具体项目需求自行设定。其中,积分商店1的商品多为稀有资源,积分商店2的商品多为普通资源。
5.3 实际应用
1)【明日方舟】的黄票和绿票
一般情况下,玩家得到5-6星干员时返还黄票(稀有积分),得到1-4星干员时返还绿票(普通积分),抽卡概率和返还数值如下:
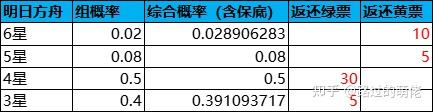
寻访凭证(抽奖券)的兑换价格为258/38张黄票或450张绿票,即G1=258/38,G2=450。由此可逆向推导出F1、F2、k1、k2等数值,如下所示:
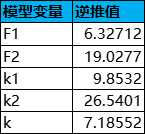
每次抽卡消耗为600合成玉,根据1源石=180合成玉=135理智(体力),600合成玉可换算为450理智,以理智作为标准价值单位,则C=450,每张黄票的价值为C/G1≈66.28,每张绿票的价值为C/G2≈1。
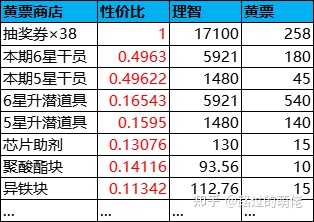
关于黄票商店,虽然明面上商品没有划分档次,但可根据性价比的不同进行人为划分。1档商品为抽奖券,性价比为1,有限购上限,搬空需258张黄票,折算抽奖次数为258×k1/G1=376;2档商品为本期干员,性价比约为0.5,有限购上限,搬空需225张黄票,折算抽奖次数为225×k1/G1=328 ;3档商品为升潜道具,性价比约为0.16,有限购上限,搬空需1360张黄票,折算抽奖次数为1360×k1/G1=1984;4档商品为培养道具,性价比约为0.13,无限购上限。
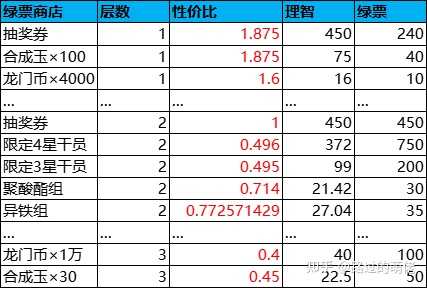
关于绿票商店,明面上商品直接划分为三个档位。1档商品的性价比为1.5~2,有限购上限,搬空需1490张绿票,折算抽奖次数为1490×k2/G2=88;2档商品的性价比为0.5~1,有限购上限,搬空需8800张绿票,折算抽奖次数为8800×k2/G2=522;3档商品的性价比为0.4~0.45,无限购上限。
2)【原神】的星辉和星尘
一般情况下,玩家得到4-5星时返还星辉(稀有积分),得到3星时返还星尘(普通积分),抽卡概率和返还数值如下:
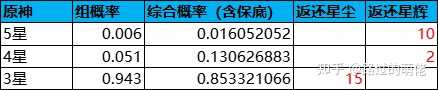
纠缠之源(抽奖券)的兑换价格为5个星辉或75个星尘,即G1=5,G2=75。由此可逆向推导出F1、F2、k1、k2等数值,如下所示:
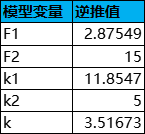
每次抽卡消耗为160原石,根据1原石=0.45树脂(体力),160原石可换算为72树脂,以树脂作为标准价值单位,则C=72,每个星辉的价值为C/G1=14.4,每个星尘的价值为C/G2=0.96。
2023/3/26 20:27 更正:下面这段关于培养素材的价值树脂的推导过程存在逻辑性错误(不要看,看了请忘掉),对资源价值分析有兴趣的话可查看本人的最新作品:【原神】的经济数值模型分析。
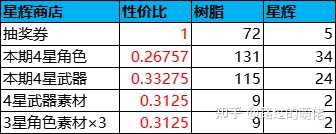
关于培养素材的价值树脂,首先看其主要获取途径(打怪掉落),然后以最高世界等级为前提,统计每天掉落数量。经过粗略统计,特定4星武器素材的每天掉落数量约为20,特定3星角色素材的每天掉落数量约为60。根据1树脂=8分钟,4星武器素材的价值树脂为24×60/20/8=9,3星角色素材的价值树脂为24×60/60/8=3。由于武器素材和角色素材的合成公式为3合1,于是3星武器素材的价值树脂为9/3=1,2星角色素材的价值树脂为3/3=1。关于星辉商店,1档商品为抽奖券,性价比为1,无限购上限,每兑换1张抽奖券所需抽奖次数为k1≈12;2档商品为本期角色和武器,性价比约为0.3,有限购上限,搬空需188个星辉,折算抽奖次数为188×k1/G1=446;3档商品为武器素材和角色素材,性价比约为0.3,有限购上限,搬空需594个星辉,折算抽奖次数为594×k1/G1=1408。 对比【明日方舟】的黄票商店,最显著的差异就是星辉商店的1档商品(抽奖券)没有限购上限,在一定程度上会影响重氪玩家的消费决策。
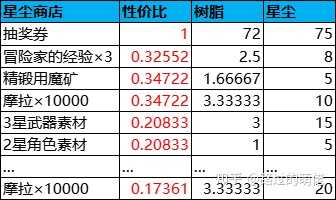
关于星尘商店,1档商品为抽奖券,性价比为1,有限购上限,搬空需750个星尘,折算抽奖次数为750×k2/G2=50;2档商品为经验、魔矿和摩拉,性价比约为0.35,有限购上限,搬空需1300个星尘,折算抽奖次数为1300×k2/G2=87;3档商品为武器素材和角色素材,性价比约为0.2,有限购上限,搬空需4740个星尘,折算抽奖次数为4740×k2/G2=316;4档商品为无限摩拉,性价比约为0.17,无限购上限。
六、 动态奖池
6.1 基础概念
在介绍动态奖池之前,首先要理解什么是奖池,虽然前文也有稍微提及奖池的概念,不过并未给出具体定义,以下是本节关于奖池、静态奖池、动态奖池的定义:
奖池:一组随机奖品的有限集合,可记为P={(奖品i, 概率i)|i=1,2,...,N},概率总和为1。静态奖池:奖品概率不随抽奖次数的积累而变化的奖池。
动态奖池:奖品概率会随抽奖次数的积累而变化的奖池。
根据上述定义,动态奖池的自变量为抽奖次数,因变量为奖品概率。奖品的变化可解释为奖品概率的变化,比如奖品A变成奖品B可解释为{(A, P*), (B, 0),...}→{(A, 0), (B, P*),...}。
前文提到的保底机制下的奖池其实就是一种动态奖池。由于奖品概率总和为1,保底大奖的概率提升必然伴随其余奖品的概率下降。其概率变化规则采用「圆桌理论」,即优先剔除稀有度低的奖品概率。以【明日方舟】为例,寻访卡池的6星保底为PRD保底模型PRD-GT(50, 99, 0.02, 0.02),5星、4星、3星的基础概率分别为0.08、0.5、0.4,则关于抽奖次数的奖品概率分布如下:

6.2 几种常见动态奖池
1)限量奖池
按照人群特征,限量可分为全服限量、公会限量、个人限量等;按照时间特征,限量可分为永久限量、活动限量、每周限量、每日限量等。限量奖品的中奖概率P依赖于其剩余库存量L,当L>0时,P=P*;当L=0时,P=0。在程序上,这里有两种处理方法:其一是奖品跳转,数值表现为跳转奖品的中奖概率增加P*;其二是概率权重清零,数值表现为其余奖品的中奖概率增加P*的加权平均值。典型例子有:全服限量实物抽奖、个人限量道具抽奖、资源每日掉落上限等。
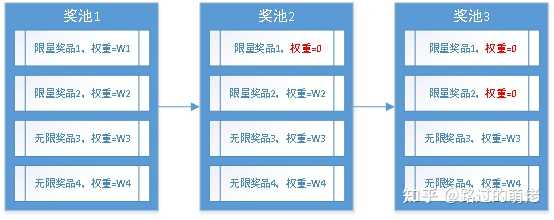
2)存储奖池
现有一个货币存储池,初始存储值为S0,存储下限为S_Min,存储上限为S_Max。设当前货币存储值为S,则活动开始时S=S0,全服玩家每次抽奖时S增加ΔS,玩家每次抽奖有几率P获得数量为S×α的货币,同时S减少S×α,0<α<1。

对于该数值模型,每次抽奖获得货币的期望值为S×α×P,显然S越大,收益期望越高,这是不公平的。为了保证相对公平,一般会针对P关于S的变化进行分段取值,使得P和S呈反比例关系。
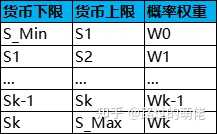
举个例子,假设货币存储池的货币类型与抽奖消耗的货币一致,S0=10000,S_Min=5000,S_Max=20000,每次抽奖消耗货币为50,ΔS=10,那么S从S_Min到S_Max的最少累计抽奖次数为(S_Max-S_Min)/ΔS=1500。我们希望1500抽以内有99.99%的把握至少能抽到一次货币,即1-(1-P)^1500>0.9999,解得P≥0.0062。我们希望每次抽奖获得货币的期望值约为抽奖消耗货币的20%,即S×α×P≈50×20%,令S=(S_Min+S_Max)/2=12500,P=0.0062,解得α≈0.13,为了使数值美观,可取α=0.15。
随机奖品中,15%货币奖池的综合概率为P=0.0062(概率权重=62),其余奖品的综合概率为1-P=0.9938(概率权重=9938),综合价值约为消耗货币的80%,即50×80%=40左右。对S的取值范围[5000,20000]平均划分为15个区间,P的分段取值如下,且货币期望=S×α×P≈(货币下限+货币上限)/2×0.15×概率权重/(概率权重+9938),其余期望=40×9938/(概率权重+9938),总期望=货币期望+其余期望,性价比=总期望/50。
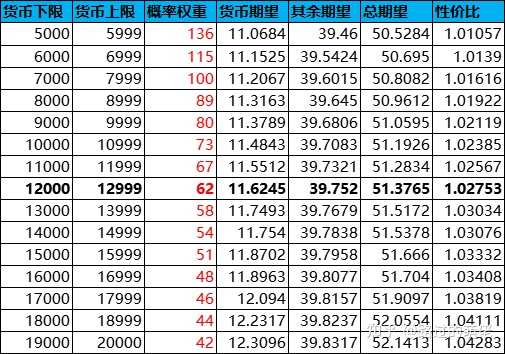
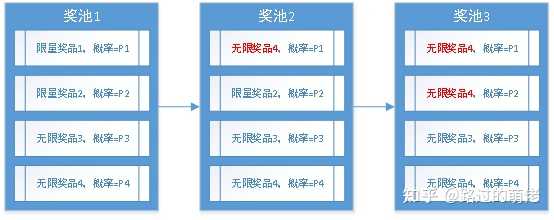
3)子母奖池
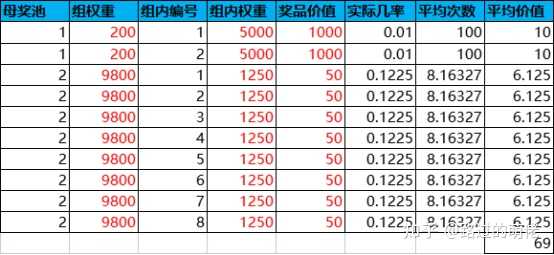
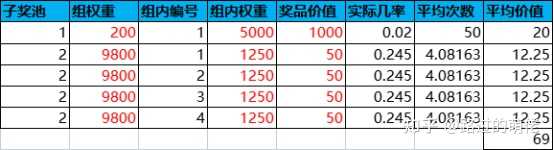
子母奖池一般为双层抽奖模型,并且采用权重记法,子奖池为母奖池在一定规则下的非空真子集。初始奖池为随机的某个子奖池,当个人抽奖次数积累到一定程度后,即可手动重置一次子奖池。当然,玩家也可选择不重置,此时的奖池则退化为静态奖池。
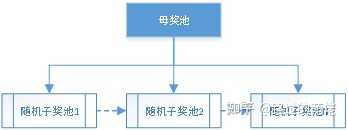
举个例子,母奖池为2个大奖+8个小奖,子奖池为随机1个大奖+随机4个小奖,则子奖池的随机组合数有C(2,1)×C(8,4)=140种。重置所需个人抽奖次数的设定可参考大奖的平均次数,比如取为50,即平均每抽中一次大奖即可获得一次重置子奖池的机会。
4)平行奖池
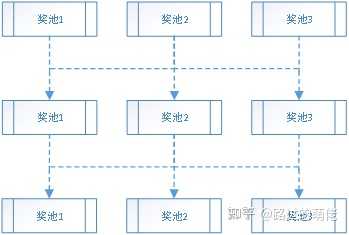
设有N个独立奖池,奖池i对应Wi张卡牌,卡牌总数为ΣWi,每一轮抽奖开始之前,对所有卡牌进行一次随机洗牌,玩家可选择翻开任意一张卡牌,若该卡牌对应奖池i,则从奖池i中随机获得一个奖品,直到翻完所有卡牌,进入下一轮抽奖。
若把每张卡牌视为一个个独立奖品,则平行奖池相当于一种特殊的限量奖池。若每次翻开一张卡牌就放回去重新洗牌,则此时的奖池为双层抽奖模型下的静态奖池,Wi为奖励组i对应的权重。 平行奖池的特征是随机洗牌和不放回抽奖。这其实也是一种保底机制,保证了每轮抽奖必然能抽到一定次数的大奖。
举个例子,现有一个翻牌抽奖活动,共有10张卡牌,其中有1张金卡和9张银卡,金卡对应稀有奖励组,银卡对应普通奖励组。
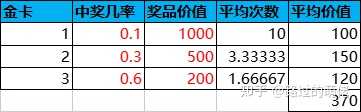
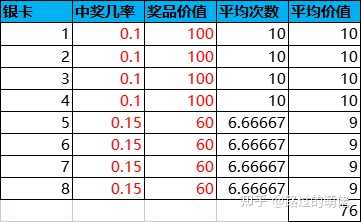
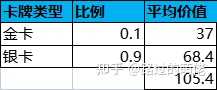
设每次抽奖消耗为100钻石,玩家在实际抽奖过程中,一旦抽中金卡,那么剩下的卡牌只有银卡。此时,玩家若继续选择翻牌,则必然是亏损的,这不利于小R用户的继续消费。因此,翻牌抽奖一般会增加重置功能,即花费X钻石重置所有卡牌。X的设定要参考抽中金卡的前提下继续抽完剩余银卡的总亏损。
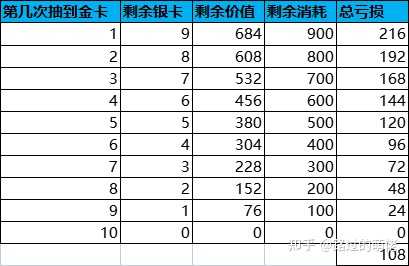
取X为100,介于96和120之间,即5次以内抽到金卡选择重置是划算的,6次以上抽到金卡选择重置是亏损的。增加重置功能之后,抽中金卡的平均次数小于或等于10,平均次数的多少取决于玩家的重置方案。若一直不使用重置功能,则抽中金卡的平均次数为10;若每次抽中金卡后立即重置功能,则抽中金卡的平均次数达到最小值。
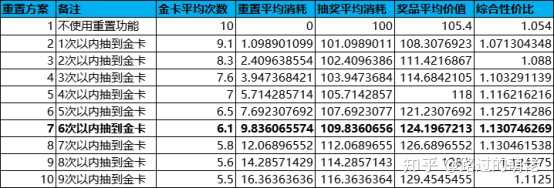
从综合性价比来看,最佳重置方案是「6次以内抽到金卡选择重置」。这里说明一下,金卡平均次数利用古典概型来求解,每轮抽奖第几次抽到金卡都是等概率的,总共有10种情况。因此,金卡平均次数=所有情况的翻牌总数/金卡总数。以「6次以内抽到金卡」为例,金卡平均次数=(1+2+3+4+5+6+10+10+10+10)/10=6.1。另外,重置平均消耗=X×P(6次以内抽到金卡)/每轮抽奖次数=100×0.6/6.1≈9.836。至于其它数据的计算就不多加说明了。
5)进阶奖池
设有N个奖池,初始奖池为1阶奖池,每次抽奖有Pi的概率从i阶奖池进阶为i+1阶奖池,i=1, 2, ..., N。这里的N+1阶奖池表示1阶奖池。一般而言,i阶奖池的平均价值低于i+1阶奖池的平均价值。于是,i阶奖池的平均次数大于i+1阶奖池的平均次数,即1/Pi>1>Pi+1,则Pi<Pi+1。也就是说,奖池的进阶概率是递增的。
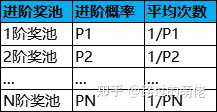

举个例子,设有1-4阶奖池,抽中稀有奖励则进入下一阶奖池,即Pi=P(抽中i阶奖池的稀有奖励)。每次抽奖消耗为100,数值设定如下表所示:
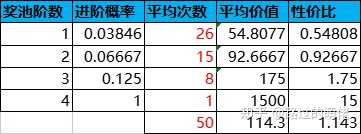
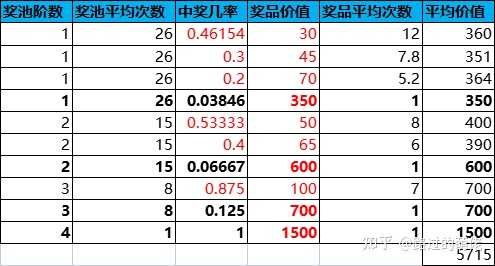
根据上述表格,抽奖性价比随奖池阶数的增加而递增,低阶奖池的性价比通常小于1,高阶奖池的性价比大于1,最高阶奖池的性价比是极高的。因此,进阶奖池有一定的付费门槛,主要面向付费用户。
七、 拓展与延伸
本质上,广义的抽奖是一种「以小博大」的随机性体验。经过设计和糅合,这种体验可以渗透到游戏中的各个系统,比如战斗、养成、玩法等。在游戏中,随机性虽然提供了丰富的多变性,但也难免伴随着一定程度的不可控性。因此,我们在设计游戏的随机性体验时,也要考虑是否对随机性加入人为干预,避免随机性失控而对游戏的本质体验造成严重的负面影响。
7.1 随机性指标
1)随机幅度
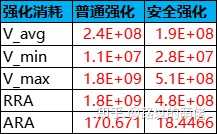
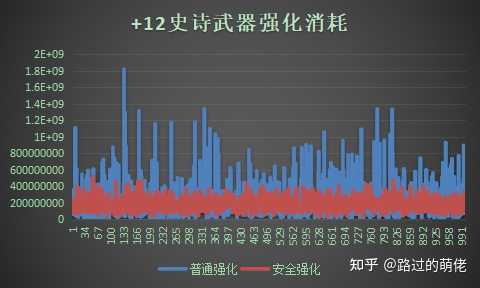
随机幅度(RA)是指一个随机过程的最大效益(V_max)和最小效益(V_min)的差距,可分为绝对随机幅度和相对随机幅度。比如一次抽奖的最好奖品价值为1000,最差奖品价值为50,每次抽奖消耗为100,则V_max=1000-100=900,V_min=50-100=-50,ARA=900-(-50)=950,RRA=+∞。
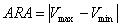
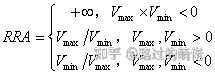
2)随机频次
随机频次是指一个随机过程在某个时间段内发生的总次数。比如一次十连抽相当于10次单抽,随机频次为10。
假设某个随机过程A1重复执行n次形成一个复合随机过程An,记An的随机幅度为RAn,则有:
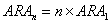
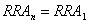
3)概率分布
一个复合随机过程An的概率分布为(P1, P2, ... ,Pn),若P1=P2=...=Pn,则An为静态概率分布,否则为动态概率分布。比如直接/PRD保底机制下的n次抽奖过程就是动态概率分布。
7.2 随机性控制
适度的随机性能让游戏体验变得丰富有趣,但失控的随机性也会让游戏体验变得糟糕透顶。随机性失控的根本原因是随机幅度过大而造成游戏体验变质。
1)控制随机幅度
2)增加随机频次
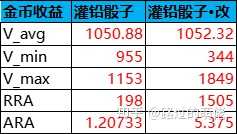
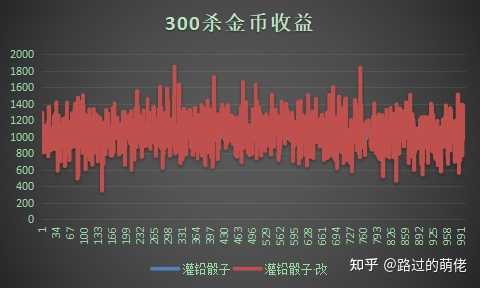
3)动态概率分布
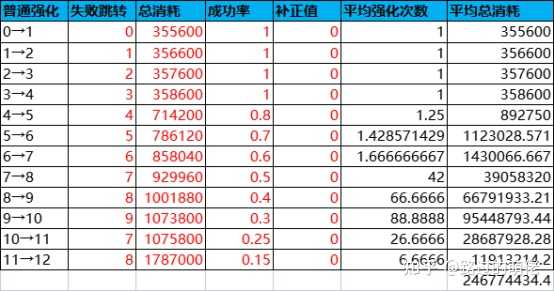
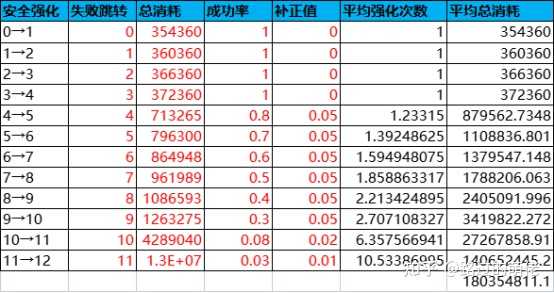
八、VBA代码附录
Sub 模拟抽奖()
Dim N As Integer
N = 200
Call 无保底(0.02, N)
Call 直接保底(0, 100, 0.016, N)
Call PRD保底(57, 156, 0.01, 0.01, N)
End Sub
Sub 无保底(p As Double, N As Integer)
Dim i As Integer
Dim k As Integer
k = 0
For i = 1 To N
再抽一次:
k = k + 1
If Rnd < p Then
Sheet1.Range("A" & i + 1) = k
k = 0
Else
GoTo 再抽一次
End If
Next
End Sub
Sub 直接保底(A As Integer, B As Integer, p As Double, N As Integer)
Dim i As Integer
Dim T As Integer
Dim k As Integer
T = 1
k = 0
For i = 1 To N
再抽一次:
k = k + 1
If T <= A Then
T = T + 1
GoTo 再抽一次
ElseIf T < B Then
If Rnd < p Then
Sheet1.Range("B" & i + 1) = k
T = 1
k = 0
Else
T = T + 1
GoTo 再抽一次
End If
Else
Sheet1.Range("B" & i + 1) = k
T = 1
k = 0
End If
Next
End Sub
Sub PRD保底(A As Integer, B As Integer, p As Double, pp As Double, N As Integer)
Dim i As Integer
Dim T As Integer
Dim k As Integer
T = 1
k = 0
For i = 1 To N
再抽一次:
k = k + 1
If T <= A Then
If Rnd < p Then
Sheet1.Range("C" & i + 1) = k
T = 1
k = 0
Else
T = T + 1
GoTo 再抽一次
End If
ElseIf T < B Then
If Rnd < p + (T - A) * pp Then
Sheet1.Range("C" & i + 1) = k
T = 1
k = 0
Else
T = T + 1
GoTo 再抽一次
End If
Else
Sheet1.Range("C" & i + 1) = k
T = 1
k = 0
End If
Next
End Sub











