驚呆了,這不是一道小學數學的題目嗎?題目如果是 1+0.9+0.09+0.009+0.0009... 和 2 比較那還差不多,而竟然是 1+0.1+0.01+0.001+0.0001...,就是 1.1111111111... 啊,也太誇張了吧,1.2、1.1111111112、1.3、1.4、1.5 都沒到,怎麽可能到達 2。看來得給題主補補小學數學了。 請翻開人教版數學四年級下冊課本 35 頁和 41 頁,好好復習復習。
① 小數的表示
開啟 35 頁(見圖1),「做一做」中習題看到沒,這就是小數各數位組成的概念,對於題目的:
1+0.1+0.01+0.001+0.0001...
就是1個一,1個十分之一,1個百分之一,1個千分之一,1個萬分之一...的和,這正是無限小數各數位的組成,即:
1.\dot{1}=1.111111... =1+0.1+0.01+0.001...
顯然,這是一個 迴圈小數 。 1.\dot{1} 和 2 誰更大呢,也就是 1.1111111111... 和 2 比較誰大誰小,你會判斷了嗎?
② 小數的大小比較
方法一(直接比較):
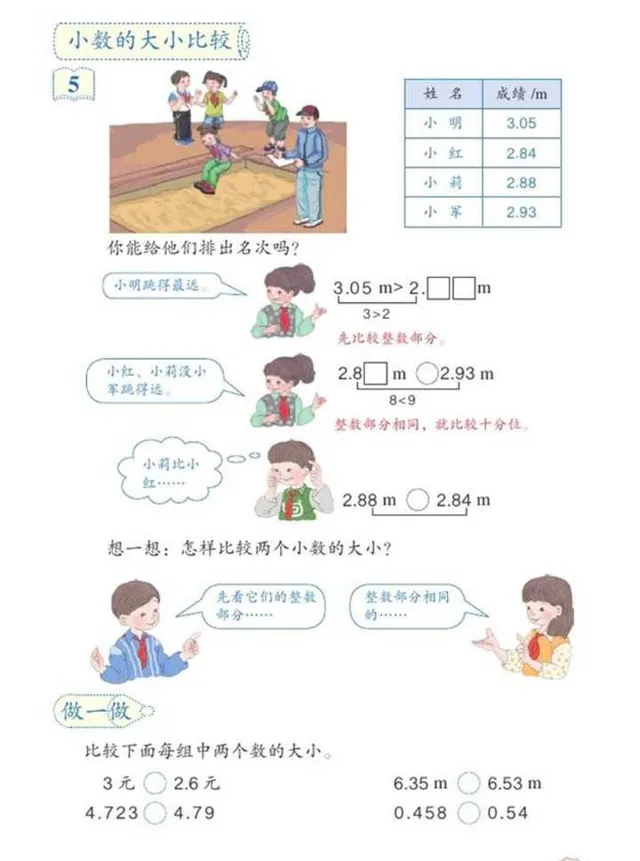
翻到 41 頁(見圖2),復習怎麽比較小數大小 ,先比較整數部份,整數部份相同就比較十分位,十分位相同就比較百分位,依此類推。
題目要比較1.\dot{1} 和 2 的大小關系, 顯然整數部份 1 比 2 要小,而且十分位的數位 1 比 9 小 [註:因為1.111...為迴圈小數,我們要再判斷此小數下一位是不是數位9],故 1.\dot{1} < 2。
我們還可以使用小數性質和數位大小關系來 更嚴格地證明以上大小關系 :
由 0.0\dot{1}\leq0.1, 得 1.\dot{1}=1.1+0.0\dot{1}\leq1.1+0.1=1.2<2。
練習題:我們已知圓周率\pi 的具體數值為3.1415926... ,那麽3.1415926... < 4 和1.\dot{1} < 2 比較的形式一樣嗎?你能說出3.1415926... 和4 之間的一個數位嗎?如何用上面的證明方法證明3.1415926... < 4 (大家動手試一試)?
方法二(化成分數比較):
那萬一碰到類似 0.\dot{9} 和 1 比較的情況呢?
別急,請開啟人教版五年級下冊課本第 77 頁(見圖3), 復習怎麽將小數轉為分數,然後再比較大小。
我們繼續拿 1.\dot{1} 和 2 比較作例子說明:
由\frac{1}{9}=0.\dot{1} ,得 1.\dot{1}=1+\frac{1}{9}=\frac{10}{9}<2,
即 1+0.1+0.01+0.001+0.0001...<2。
練習題:0.\dot{9} 如何轉化為分數和 1 比較呢?


③ 拓展內容 (小學超綱知識,可跳過,若感興趣可進一步鉆研)
(1)如何嚴謹證明 0.\dot{9} 和 1 相等
上面提到的用分數論證 0.\dot{9} 和 1 相等的證明方法是對的嗎?有沒有更嚴謹的證明方法呢?請參見知乎上已有的詳細解答:為什麽 0.9 的迴圈等於 1?,如何嚴謹地證明 0.9999…=1?。這裏不再贅述。
註:數學證明各有不同的嚴謹性、背景假設和目標受眾。對於非數學研究人員來說,將 0.\dot{9} 轉化為分數相乘等於1的形式,或將整體看作一個未知變量乘10之後求差得到未知變量為1的證明形式,均是正確的證明方法;而對於基礎數學研究來說,對 0.\dot{9} = 1 最嚴謹的論證則需要用到實數理論。這些論證形式在奧數教材或數學期刊中都有給出過, 維基詞條上更是有詞條 「0.999...」( https://en.wikipedia.org/wiki/0.999... ) , 從最簡單到最復雜的近十種證明,都全部列出來,本詞條上也強調這些證明都是正確的,只是嚴謹性和受眾目標各不同而已 。法國數學家 Jean-Paul Delahaye 也發表過文章【0.999...=1?】(0.999...= 1?),系統性地介紹了從初等數學到高等數學的各種論證形式。
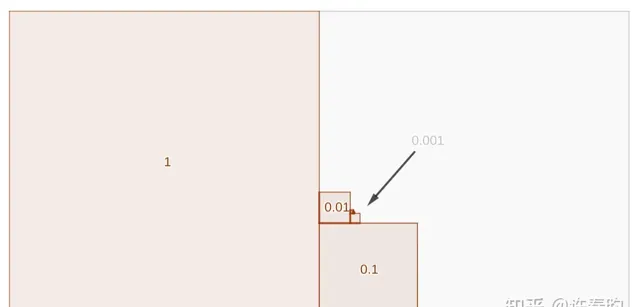
(2)用圖形直觀表示 1.\dot{1}
如圖4所示,最大的正方形面積為單位1,小一點是0.1(邊長等於單位1對應正方形邊長的 \frac{1}{\sqrt{10}} ),再小一點的是0.01(邊長等於0.1對應正方形邊長的 \frac{1}{\sqrt{10}} ),依次畫下去, 全部粉紅色部份就代表小數 1.\dot{1} 的大小 。
白色部份則是第二個單位1的正方形剩下的空間,從直觀上看 1.\dot{1} 比 2 小得多,而且越到後面的正方形越擠到下面箭頭位置的角落中,1.\dot{1} 也無法收斂於 2 ,畢竟中間還有 1.112,1.12,1.2,1.\dot{2},1.\dot{9} 等等數位。