一般來講阻力都是與運動速度或速度平方成正比。一個比較常見的流體阻力公式是
F_D = \frac{1}{2} \rho v^2 C_D A ,
其中 \rho 是流體密度,C_D 是阻力系數, A 是橫截面積。
總之 F_D = Cv^2 ,把別的全寫成常數就好了。值得註意的是這裏我們把物體完全考慮成了橫截面相同的,如果飛行中變了,那阻力自然也變了。
至於別的東西就跟平常沒啥兩樣了。這裏做個常規的拋物線的例子吧。
u 為起始速度, \theta 為與水平面的起始角度。執行中只受兩個力,重力和阻力。用常規方法設定參照系,原點為拋物線起點。
合力: \vec F = \vec F_g + \vec F_D = \begin{pmatrix} -Cv_x^2 \\ -mg - Cv_y^2 \end{pmatrix} = m \vec a = m \frac{d\vec v}{dt} ,
\Rightarrow \frac{d v_x}{dt} = -C'v_x^2 ; \frac{dv_y}{dt} = -g-C'v_y^2 , C' = \frac{C}{m} ,另一個常數。
\Rightarrow \int_{u \cdot cos(\theta)}^{v_x} - \frac{1}{v_x'^2} dv_x' = \int_{0}^{t} C' dt' ; \int_{u \cdot sin(\theta)}^{v_y} \frac{dv_y'}{1 + cv_y'^2} = \int_{0}^{t} -g dt' , c = \frac{C'}{g} ,同樣常數而已。
第一個是
[\frac{1}{v_x'}]_{u \cdot cos(\theta)}^{v_x} =\frac{1}{v_x} - \frac{1}{u \cdot cos(\theta)}= C't ,
第二個
\int_{u \cdot sin(\theta)}^{v_y} \frac{dv_y'}{1 + cv_y'^2} = \int_{0}^{t} -g dt' \\ \Rightarrow tan(\vartheta) = \sqrt{c} v_y' \Rightarrow sec^2(\vartheta) d\vartheta = \sqrt{c} d v_y' \\ \Rightarrow\int \frac{1}{\sqrt{c}}\frac{sec^2(\vartheta) d\vartheta}{1 + tan^2(\vartheta)} = \int \frac{1}{\sqrt{c}}\frac{sec^2(\vartheta) d\vartheta}{sec^2(\vartheta)} = \frac{\vartheta}{\sqrt c} ,
因此
[\frac{arctan(\sqrt{c}v_y')}{\sqrt c}]_{u \cdot sin(\theta)}^{v_y} = \frac{arctan(\sqrt{c}v_y) - arctan(\sqrt{c} \cdot u \cdot sin(\theta))}{\sqrt c} = -gt ,
由此我們就有了
\vec v = \begin{pmatrix} \frac{u \cdot cos(\theta)}{1+ u \cdot cos(\theta) C't} \\ \frac{1}{\sqrt c} \cdot tan[\ arctan(\sqrt{c} \cdot u \cdot sin(\theta)) - \sqrt{c} gt\ ] \end{pmatrix} ,稍微整理一下
\vec v = \begin{pmatrix} \frac{1}{1+ u \cdot cos(\theta) C't} u \cdot cos(\theta) \\ \frac{1}{{1 + \sqrt{c} \cdot u \cdot sin(\theta) tan(\sqrt{c}gt)}} (u \cdot sin(\theta)- \frac{1}{\sqrt c}tan(\sqrt{c}gt)) \end{pmatrix} ,
可以看出來隨著時間的增加,x方向上的速度逐漸減小,
而y方向的話也是一個遞減的關系,大概的走勢可以用
\frac{1 - tan(x)}{1 + tan(x)} 來類比,只是系數不一樣。可以看出來跟只受重力時的線性降速是有區別的。(值得一提的是計算中物體向上運動,因此我們用的阻力是向下的,但是如果物體開始下落後,阻力應該是向上的,這個變化在這裏是表現不出來的)
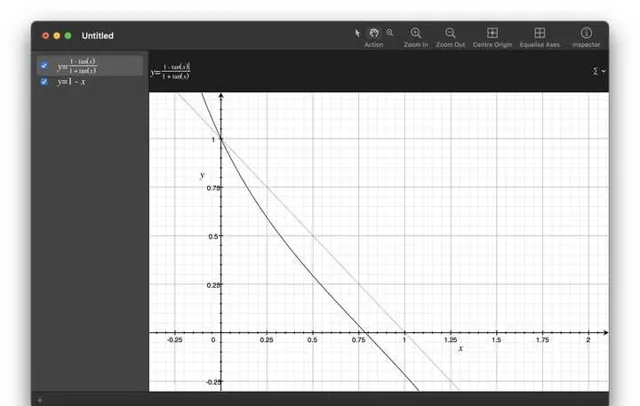
同時,可以看出來當阻力小的時候( C' 和 c 都小的時候), \vec v 會收斂到
\vec v = \begin{pmatrix} u \cdot cos(\theta) \\ u \cdot sin(\theta)- gt \end{pmatrix} ,而這個就是只受重力的時候。
那麽運動狀態就是 \vec v 再做一次積分,大致明白是個什麽情況就好了,這裏就暫時不繼續往下寫了。









