人類制造的最不可思議的機器有哪些？

嚴格來說，MOSFET其實是晶體管的一種。

這三樣東西都可以被叫做 三極管(Triode) ，一種電氣器件。

這三樣東西在歷史上都曾經被用作數位電路的基本部份，先是電子管，然後是BJT晶體管，然後是MOSFET，現在常用在積體電路裏面的就是MOSFET了，因為它能做的特別小，小到幾十奈米（怎麽做出來這種很小很小的三極管我後面會介紹一下）。具體它們怎麽工作的大家不用知道，涉及半導體物理，這個我也不是很懂，只需要知道它們的功能：能夠做成一個電子開關。電子開關就是能用電訊號控制電路通斷的一個開關。啥意思呢，假設你家裏現在裝了一盞燈，如果它裝了一個電子開關，那麽你就需要給這盞燈的開關施加一個電壓才能把燈開啟。這顯得特別蠢，因為為啥我不直接把電壓加到燈泡上呢？這是因為：我只需要給這個開關施加一個很小的電壓就能讓開關開啟，而這個電壓未必能足夠讓燈亮起來，這是三級管的放大作用，不過在數位電路裏邊不會用到；另一個原因是有一類電子開關是反著來的，高電壓斷路，低電壓接通。這兩種電子開關就是我們用來做電腦的玩意兒了。

用電子開關去焊一台電腦出來貌似很遙不可及，不過現在我們手頭有了電子開關，我們可以做一些簡單的東西了：

邏輯閘

大家耳熟能詳的一句話叫做電腦只認識0和1，這個是什麽意思呢。電腦裏面的數位電路是基於某一種特殊的 布爾代數 的，布爾代數這個名字聽上去有點吊吊的，但是這種特殊的布爾代數其實就是在0和1上的運算，只有0和1，這個概念和二進制有點不一樣，二進制是一種計數法，二元布爾代數只有0和1兩個東西，沒有2啊3的，也沒有10，11。電腦使用布爾代數的原因倒是不難想，因為高電平胡低電平（電平這個詞大家就理解成一個電壓標準好了）天然適合表示0和1，你要它表示一個新的數，你得弄個中電平出來，這個東西在電路設計裏面就很麻煩了。不如用高低電平來表示，這樣直接用電路通斷就能很方便的控制了。 布爾代數這玩意牛逼就牛逼在弄出布爾代數的時候可還沒有電腦啊，那個時候才1850年，研究這東西沒有物理背景的，誰能想到這玩意以後因為電腦大紅大紫了呢。很多現在研究的數學問題也沒有什麽物理背景，千萬別去嘲諷數學家們弄這個，沒準哪天就用上了。

感謝

的補充：

"給一點糾正和補充吧，布爾代數不必須只有0和1，詳細參考近世代數和/或離散數學的內容。邏輯電路使用的是一個特殊的布爾代數系統。"

實在抱歉，不過不影響理解我後面的內容就暫時不改了，大家知道是錯的就好。

布爾代數裏面最基本的三個運算是與、或、非，與和或是二元運算，代表著它需要使用兩個數來算出一個數，非是一元運算，代表著它只需要一個數就能算答案了我把這三個運算的真值表列在下面：

與：

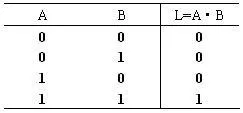
或：

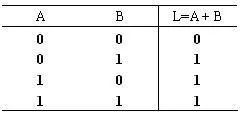
非：

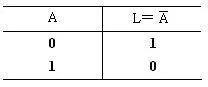
這三個運算構成了一個布爾運算的完備集（是這個詞嗎？我離散數學的書不在手邊查不到...)，意思就是只要用這三個運算的組合，就能完成這世界上所有可能的布爾運算，你怎麽定義這個運算都可以。其實使用一點簡單的代數知識我們可以證明其實只要非和與，或者非和或，也能做到。

那麽，如果我們想要實作一個運算，比如一個三元布爾代數運算，就是有三個數輸入，一個數輸出的運算，我們只需要用一大堆與或非，然後湊吧湊吧就能把這個運算寫出來。這個功能其實就很強大啦，比如，我們想要做一個四位二進制加法，四位數加四位數，輸出一個四位數加一個進位，我們只需要五個八元布爾代數運算就行了，每一個運算對應答案上的一位，還有一個對應進位。

為了實作這樣強大的功能，我們只需要做出三種對應最基本的三種運算的電子器件，我們再使用這些東西組合一下，就能實作非常復雜的邏輯了對吧？這些對應最基本運算的電子器件，就叫做 邏輯閘(Logic Gates) 。

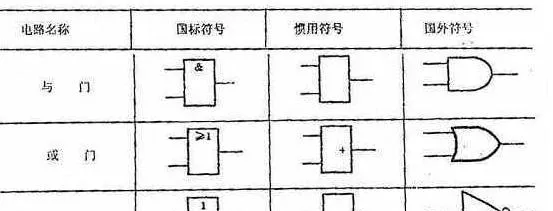
與門有兩個輸入端，兩個輸入端都是高電平的時候輸出端也是高電平，否則就是低電平，非門當輸入端是高電平的時候輸出端是低電平，輸入端是低電平的時候輸出端是高電平，或門就不用說了。

怎麽做呢？

我們最先考慮一個簡單的東西，與門。

我們回顧一下最基本的初中物理：串聯和並聯

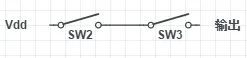
恩，這是兩個開關串連在一起，最左邊接電壓源。我們發現只有兩個開關都接通的時候，輸出端是高電壓。非常合適。我們把這兩個開關變成上面說的，通電就通的電子開關，分別引出兩個輸入端，我們就有一個與門了。

但其實這還不夠，在輸出為低電平的時候，輸出端不能像現在一樣啥都不接，得接一個低電平，所以這只是一個與門的一半，另外一半是這樣的：

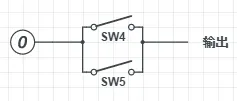
0這一端表示接地，這兩個電子開關是那種反著來的電子開關，加電壓就斷，不加電才通。

我們把這兩個東西寫到一起來。

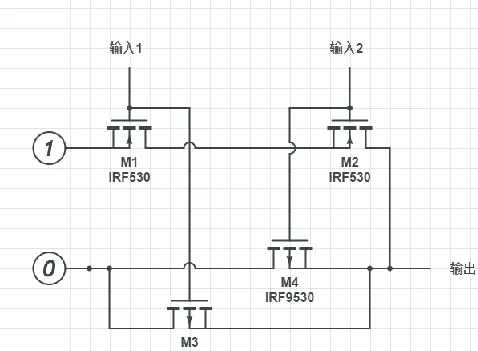
開關變了個樣子，大家不要激動，忽略那些參數，箭頭向下指的是PMOS，就是M3和M4，相當於我們說的反著來的電子開關。箭頭向上指的那兩個(M1和M2)是NMOS，相當於我們說的正著來的電子開關。這兩種MOS一起組成的電路就叫 CMOS 電路。我們現在就有了一個與門。

但其實作實中也不是這樣做的。因為PMOS和NMOS本身的一些電氣特性，這樣做出來的與門穩定性很差，現實中我們是這樣做的：

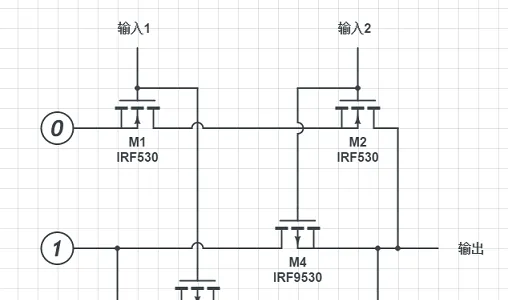
把0和1反一下。

這樣做出來的輸出正好和與門是反過來的，相當於與門後面跟了一個非門，所以它叫 與非門(NAND Gate) ，寫成符號的話是這樣的：

它很牛逼，原因如下：

這是一個非門：

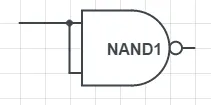
這是一個與門：

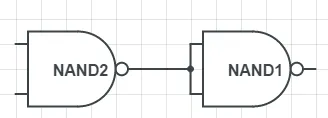
這是一個或門：

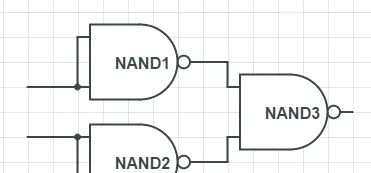
根據上面的內容，只要有這三個門就能完成所有的二元布爾運算。也就是說，它一個門就能搞定所有的二元布爾運算。

實際上在操作中我們是直接使用原理相似的或非門和非門去搭電路，而不是用與非門做出來的這種復雜玩意兒，但是這也足夠神奇了不是麽。

接下來我們就可以嘗試做做最簡單的小算盤了。

全加器(Full Adder)

全加器是用來計算加法的電路，顧名思義。既然有全加器，那麽就應該有對應的半加器。半加器是不帶進位的加法，如果是一個一位半加器，就只有兩位輸入，一位輸出，如果有進位的話就丟棄掉。全加器表示的是帶進位的加法。一位全加器有三個輸入端，除了兩個加數以外還有一位的進位。對應的，它也有兩個輸出，一個代表的是這一位的結果，另外一位是進位。多了進位的好處是，如果我們把足夠多的全加器串聯起來，就能做成一個多位加法器，像是這樣：

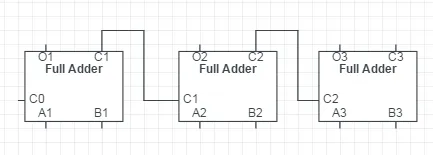
這是個三位的加法器，A和B表示輸入，O表示輸出。當然也可以往後面不斷接更多的全加器，變成4位元5位6位....等等。加法器其實是所有運算電路的基本元件，減法器和加法器基本上是一樣的，乘法其實是移位和加法的結合，除法是移位和減法的結合（大家想想運算的時候列豎式是怎麽列的？）。

說起來全加器的內部結構也是挺簡單的。不過首先我們需要一些分析，這裏可能講得比較晦澀，如果大家不想看的話直接往後跳到下一部份就好了。

全加器一共有兩個輸出，O和C，分別代表結果和進位。

O在三個輸入中有一個為1或者都為1時為1，其余情況為0，相當於在輸入中數1的個數，如果是奇數就為1，如果是偶數就為0。很湊巧的是，我們有一個專門的邏輯運算來處理這個問題，叫異或(XOR)，它是一個二元運算，如果兩個值相同則輸出0，兩個值不同輸出1。寫成公式的話就是下面這個樣子。

a \oplus b = (\bar{a}\wedge \bar{b})\vee (a\wedge b)

圓圈裏一個加號就是XOR，上加橫線表示not，\vee 表示或，這個符號上下顛倒表示與。

其實我們也是有專門處理異或運算的門的，用符號表示成這樣：

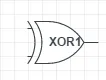
那麽輸出端O的電路可以這麽畫：

C在三個輸入中有兩個以上為1時為1，其余情況為0。

我們可以把它寫成這個樣子：

C = (A \wedge B) \vee (C_0\wedge (A\vee B))

看上去超級復雜，其實邏輯很好理解，如果A和B都是1，A\wedge B 等於1,，C就等於1，接下來一個部份是來考慮A和B不都等於1的情況的，這個時候只要AB其中之一等於1，C0也等於1，C輸出也是1。

我們可以把它也畫成電路：

然後把兩個部份拼在一起：

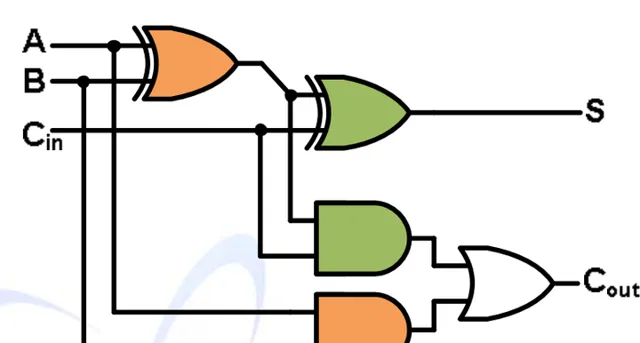
（不想畫圖了，就從課件上截了個圖...）

就是全加器啦。可能有人發現了，我們其實重用了一個門的輸出，就是O部份電路裏面的第一個異或門。這個異或門的輸出可以代替C部份電路裏面的第一個或門的輸出，結果是一樣的。

現在，如果大家有心思用開關和小燈泡當輸入和輸出器件的話，我們已經可以做成一個只能算二進制加法的小算盤了。

離電腦還真是遙遙無期啊。

接下來要簡單介紹一個很重要的部件，它是電腦實作多種功能選擇的基礎：

多路選擇器(Multiplexer，MUX)

多路選擇器，顧名思義，就是能在很多路中間選一個的元件。

最簡單的多路選擇器是這樣的：

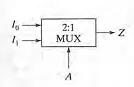
什麽意思呢，當A為0的時候Z的輸出等於I0,當A為1的時候Z的輸出等於I1。

當然它也有4:1版本,8:1版本，輸入端相應增加就是了，功能不變。下面是一個4路選擇器的門級電路圖（後面電路說明不想看可以不看），看上去有點亂，其實還蠻簡單。拿I0這條線來說，把它和A的非和B的非同時接到一個與門上，這個時候這個與門的輸出就只在A和B都為0的時候等於I0，其余時刻永遠為0了。其它路線也是一樣的，把所有路線或成一個輸出，就是多路選擇器了。

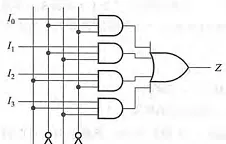
這個東西有兩個重要作用：

首先，比如你想做一個小算盤，又能做加法又能做乘法，這個時候就需要MUX出手了。你做一個開關，表示現在正在進行的運算，0的時候表示加法，1的時候表示乘法，然後做一個加法器，做一個乘法器，把輸入分別接到加法器和乘法器上，加法器和乘法器的輸出接到MUX上，控制開關接MUX的控制端，輸出就是你想要的東西了，現代電腦裏面最重要的東西是CPU，CPU裏面負責算數運算的模組叫 算術邏輯單元(Arithmetic and Logic Unit, ALU) ，可以負責很多種運算，加減乘除，或與非等等，就需要多路選擇器的控制。這個東西還可以用在記憶體裏面，比如我需要提取哪一個地址上的東西，把MUX控制端看成地址輸入，輸入端看成儲存內容輸入，輸出就是我想要的內容了。

其次，這個元件非常討懶人工程師們的喜歡。為什麽呢？假設我要做一個三元運算，有了MUX以後我再也不用費勁想哪個門應該怎麽接了，只要寫一下三元運算在所有情況下的輸出，然後再MUX的輸入上對應接上這些輸出，比如000輸出0，我就在I0的位置直接接低電平，001輸出1，我就在I1上接高電平，直接完事，都不用想的。

到了這裏我們已經把組合邏輯部份講完了，到了這裏大家可以做一些比如閏年小算盤之類的小玩意，但是離可以實用的家用電器還差得很遠很遠。

我們上面提到了一個重要的東西叫做記憶體，大家仔細想一想，其實如果沒有儲存能力的話，我們能做的東西非常有限，做個小算盤輸入還得是用開關一位一位去撥才行，連現在的小算盤上面的按鍵開關都不行，因為它也有最基本的儲存功能，在你按下鍵的時候，按鍵開關發出了一個很短暫的高電平訊號，我們還得把這個很短暫的訊號存下來，變成一個穩定的高電平才行。這個時候需要一個很重要的部件出場了： 鎖存器(Latch)

從名字上就能看出來鎖存器的功能了，把輸入鎖住，存起來。

鎖存器需要幹一些什麽呢，它作為一個最簡單的時序元件，它需要完成下面兩個簡單的任務：

1.在某一個輸入狀態之下，可以保存一個訊號，或0或1。

2.在某一個輸入狀態之下，能把其中儲存的訊號變成自己想要的訊號。

想要做一個能把一個電平存住的東西需要大家有點想象力。

先看下面這個電路：

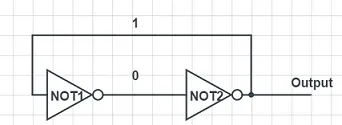
這個電路沒有輸入，但這個電路用兩個非門可以把裏面的這個1存到天荒地老，或者停電為止。而且你要是把圖上的0和1換一下，也行，這樣就變儲存0了。這個結構的好處就是，它可以用同一個結構儲存0或者1，這是所有記憶體件的基本功能。

但是光有它不夠，作為一個記憶體件，你最起碼得有一個能力就是我要你存啥你存啥，這個結構...不行。

那我們改改。

當我們需要一個輸入的時候，我們把最左邊的開關合上，把Store開關斷開，這個時候這個能儲存的電路環就不存在了，然後從左邊給輸入。然後我們把Store一合，Load一斷，這個時候就已經存上了。這個模型就可以當做一個儲存單元用了。我們只需要把它改成一個門電路的形式就好。為了以後的制造工作省點事，我們在改動過程中需要盡量使用比較少的門電路來完成這個過程。

我們先試試用一個門行不行。

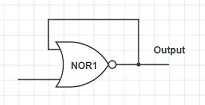
這個電路保持了上面電路的特點，如果你不給他輸入，它就能一直把裏面的東西保存到天荒地老。如果原來電路中保存的是0，輸入為1的時候儲存值就會改變成1。但是這個電路雖然能有「把儲存的訊號變成1的功能」，但是沒有一個可以穩定的完成「把儲存的訊號變成0」的功能。我們需要把這個功能給引入進來。那麽我們把電路改成下面這個樣子：

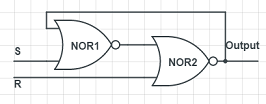
這樣，如果S保持0，R是1，就可以將保存的內容置成0了。

這個門電路結構叫做 SR鎖存器 ，其實在很多書上它還有一個非常炫酷的畫法：

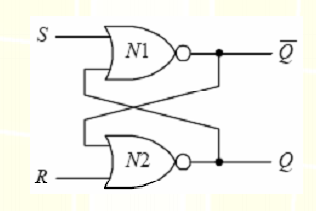
Q是輸出\bar{Q} 表示和輸出的反相，相當於輸出加一個非門。

這個鎖存器的功能是這樣的：當S和R都是0的時候，輸出是之前儲存的內容。如果S是1R是0，儲存的內容變為1，如果S是0R是1，儲存內容變為0。如果兩個都是1，此時的輸出時沒有定義的，這個器件要求大家在電路執行的時候不要這樣做，否則會被玩壞掉。

這個鎖存器是我們接下來許多各式各樣的儲存元件的基礎，比如，門控SR鎖存器：

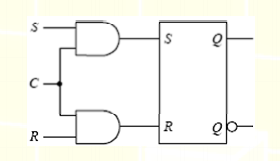
它加入了一個控制端C，相當於之前的控制開關，只有當控制端為1的時候，S和R的改變才會影響到鎖存器內部保存的訊號，這樣可以解決一部份S和R同時為1的情況。

再有D鎖存器：

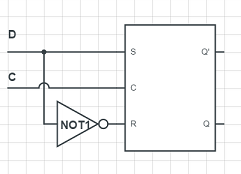
字比較小，我說一下：後面那個大元件是一個門控SR鎖存器，三個輸入端分別是S,C,R。

它用一個D輸入端取代了S和R兩個輸入端的功能。純粹靠C來控制寫入/儲存狀態，靠D來輸入，在套用上面就更加簡單了。

這些鎖存器有很多優點:用的門特別少，所以速度飛快，但是相對應的，比如在SR鎖存器中就有一個輸入組合是不能用的，而且速度再快，每個門對於電訊號的處理還是要花時間的，如果輸入變化太快，它也是會出現很多不穩定的現象的。怎麽解決呢？我們可以透過使用一種叫做 時鐘 的訊號來控制這些鎖存器工作在一個比較穩定的速度下面，還可以同步許多鎖存器的共同工作。

施工中。