这篇回答节选自我的专栏 【机器学习中的数学:概率图与随机过程】 ,我们来仔细介绍和分析一下Gibbs采样。
也欢迎关注我的知乎账号 @石溪 ,将持续发布机器学习数学基础及算法应用等方面的精彩内容。
1.Gibbs方法核心流程
在 M-H 算法的基础上,我们再介绍一下 Gibbs 采样。
吉布斯采样是一种针对高维分布的采样方法,假设我们待采样的高维目标分布为 p(z_1,z_2,z_3,...,z_m) ,吉布斯采样的目标就是从这个高维分布中采样出一组样本 z^{(1)},z^{(2)},z^{(3)},...,z^{(N)} ,使得这一组样本能够服从 m 维分布 p(z) 。
我们先约定一个记法:按照上述假设,从分布中采得的样本 z 是一个拥有 m 维属性值的样本值, z_i 表示某个样本 z 的第 i 维属性, z_{-i} 表示除开第 i 维样本外,剩余的 m-1 维属性: z_1,z_2,...,z_{i-1},z_{i+1},...,z_m
具体如何采样,核心在七个字:一维一维的采样:
那么何谓一维一维的采样呢?我们以三维随机变量 z 为例: p(z)=p(z_1,z_2,z_3)
首先在0时刻,我们给定一个初值,也就是 z^{(0)} 的三个属性的值: z^{(0)}_1,z^{(0)}_2,z^{(0)}_3
好,下面我们来看下一个时刻,也就是时刻1的采样值如何生成:
z_1^{(1)}\sim p(z_1|z_2^{(0)},z_3^{(0)})
z_2^{(1)}\sim p(z_2|z_1^{(1)},z_3^{(0)})
z_3^{(1)}\sim p(z_2|z_1^{(1)},z_2^{(1)})
这样就获得了时刻1的包含三维属性值的完整采样值。
那么接着往下递归,概况起来,通过 t 时刻的采样值递推到 t+1 时刻,也是如上述方法那样一维一维的生成采样值的各个属性:固定其他维的属性值,通过条件概率,依概率生成 t+1 时刻的某一维度的属性值。
z_1^{(t+1)}\sim p(z_1|z_2^{(t)},z_3^{(t)})
z_2^{(t+1)}\sim p(z_2|z_1^{(t+1)},z_3^{(t)})
z_3^{(t+1)}\sim p(z_2|z_1^{(t+1)},z_2^{(t+1)})
这样就由$t$时刻的采样值 z^{(t)} 得到了下一时刻 t+1 的采样值 z^{(t+1)}
按照该方法循环下去,就可以采样出 N 个样本值: z^{(1)},z^{(2)},z^{(3)},...,z^{(N)} ,丢弃掉前面一部分燃烧期的样本,剩下的样本就服从我们的目标高维分布。
2.Gibbs采样的合理性
这就是Gibbs采样的核心流程,有两个大的问题。
第一个问题是:为什么通过这种采样方法采得的样本能够服从目标分布 p(z) ?
我们拿Gibbs采样和M-H方法进行类比,我们会发现其实Gibbs采样就是M-H采样的一种特殊情况,这个结果就证明了Gibbs的可行性,注意逻辑是这样的,M-H我们已经证明是符合细致平稳条件的,而Gibbs是M-H的一种特殊情况,因此Gibbs也符合细致平稳条件,因此可行。
首先,我们采样的目标分布是 p(z) ,而我们实际使用的提议转移过程 Q 就是概率 p 本身: Q(z^*,z)=p(z_i|z_{-i}^*) ,你发现了没,在这个采样过程,好像没有接受率 \alpha 的出现。
我们重新看看接受率 \alpha(z^*,z) 的定义式:\alpha(z^*,z)=min(1,\frac{p(z^*)Q(z^*,z)}{p(z)Q(z,z^*)})
重点就在 \frac{p(z^*)Q(z^*,z)}{p(z)Q(z,z^*)} 这个式子: p(z)=p(z_i,z_{-i})=p(z_i|z_{-i})p(z_{-i})
\frac{p(z^*)Q(z^*,z)}{p(z)Q(z,z^*)}=\frac{[p(z_i^*|z_{-i}^*)p(z_{-i}^*)]p(z_i|z_{-i}^*)}{[p(z_i|z_{-i})p(z_{-i})]p(z_i^*|z_{-i})}
这个式子如何化简?我们发现,在上面的转移过程 z\rightarrow z^* 当中,我们是通过固定采样值 z 的 -i 维属性,单采 z^* 的第 i 维属性值,那么在一次属性采样前后 z_{-i} 和 z_{-i}^* 是一码事儿,那我们把上面式子中所有的 z_{-i}^* 都替换成 z_{-i} ,就有:
\frac{p(z^*)Q(z^*,z)}{p(z)Q(z,z^*)}=\frac{[p(z_i^*|z_{-i}^*)p(z_{-i}^*)]p(z_i|z_{-i}^*)}{[p(z_i|z_{-i})p(z_{-i})]p(z_i^*|z_{-i})}\\=\frac{[p(z_i^*|z_{-i})p(z_{-i})]p(z_i|z_{-i})}{[p(z_i|z_{-i})p(z_{-i})]p(z_i^*|z_{-i})}=1
也就是说Gibbs采样中的接受率 \alpha 为:
\alpha(z^*,z)=min(1,\frac{p(z^*)Q(z^*,z)}{p(z)Q(z,z^*)})=min(1,1)=1
因此满足细致平稳条件的原始等式:
p(z)Q(z,z^*)\alpha(z,z^*)=p(z^*)Q(z^*,z)\alpha(z^*,z) 就等效为:
p(z)Q(z,z^*)*1=p(z^*)Q(z^*,z)*1\Rightarrow p(z)Q(z,z^*)=p(z^*)Q(z^*,z) 其中: Q(z^*,z)=p(z_i|z_{-i}^*)
因此 p(z) 和 Q(z,z^*) 满足细致平稳条件,按照 Q 描述的状态转移过程所得到的采样样本集,在数量足够多的情况下,就近似为目标分布 p(z)
但是我们看出来了,我们把提议转移概率矩阵 Q 就定位了 p 的满条件概率,那么很显然就有一个限制条件,那就是高维分布 p 的所有满条件概率都是易于采样的。
关注 @石溪 知乎账号,分享更多机器学习数学基础精彩内容。
3.Gibbs采样代码试验
说了这么多,我们举个具体的例子,比如目标分布是一个二维的高斯分布,他的均值向量: \mu=\begin{bmatrix}3\\3\end{bmatrix} ,协方差矩阵 \Sigma=\begin{bmatrix}1&0.6\\0.6&1\end{bmatrix} ,即$z$包含两维属性 (z_1,z_2) , z \sim N(\mu, \Sigma)
我们通过吉布斯采样的方法,来获取服从上述分布的一组样本值:
很显然,这个二维高斯分布的目标分布是可以进行Gibbs采样的,因为高斯分布有一个好的性质,我们之前反复说过,那就是高斯分布的条件分布也是高斯分布,因此保证了一维一维采样的过程是顺畅的。
我们先给出二维高斯分布的条件概率分布公式:
z 包含两维属性 (z_1,z_2) , z \sim N(\mu, \Sigma) ,其中 \mu=\begin{bmatrix}\mu_1\\\mu_2\end{bmatrix} , \Sigma=\begin{bmatrix}\delta_{11}&\delta_{12}\\\delta_{21}&\delta_{22}\end{bmatrix}
那么条件分布 z_1|z_2 和 z_2|z_1 分别服从下面的形式:
z_1|z_2\sim N(\mu_1+\frac{\delta_{12}}{\delta_{22}}(z_2-\mu_2),\delta_{11}-\frac{\delta^2_{12}}{\delta_{22}})
z_2|z_1\sim N(\mu_2+\frac{\delta_{12}}{\delta_{11}}(z_1-\mu_2),\delta_{22}-\frac{\delta^2_{12}}{\delta_{11}})
这就是二维高斯分布采样过程中,逐维采样所依从的满条件分布,他是高斯分布,因此操作尤其简便,下面我们来看代码:
代码片段:
import
numpy
as
np
import
matplotlib.pyplot
as
plt
import
seaborn
seaborn
.
set
()
#依照z1|z2的条件高斯分布公式,给定z2的条件情况下采样出z1
def
p_z1_given_z2
(
z2
,
mu
,
sigma
):
mu
=
mu
[
0
]
+
sigma
[
1
][
0
]
/
sigma
[
0
][
0
]
*
(
z2
-
mu
[
1
])
sigma
=
sigma
[
0
][
0
]
-
sigma
[
1
][
0
]
**
2
/
sigma
[
1
][
1
]
return
np
.
random
.
normal
(
mu
,
sigma
)
#依照z2|z1的条件高斯分布公式,给定z1的条件情况下采样出z2
def
p_z2_given_z1
(
z1
,
mu
,
sigma
):
mu
=
mu
[
1
]
+
sigma
[
0
][
1
]
/
sigma
[
1
][
1
]
*
(
z1
-
mu
[
0
])
sigma
=
sigma
[
1
][
1
]
-
sigma
[
0
][
1
]
**
2
/
sigma
[
0
][
0
]
return
np
.
random
.
normal
(
mu
,
sigma
)
#Gibbs采样过程
def
gibbs_sampling
(
mu
,
sigma
,
samples_period
):
samples
=
np
.
zeros
((
samples_period
,
2
))
z2
=
np
.
random
.
rand
()
*
10
for
i
in
range
(
samples_period
):
z1
=
p_z1_given_z2
(
z2
,
mu
,
sigma
)
z2
=
p_z2_given_z1
(
z1
,
mu
,
sigma
)
samples
[
i
,
:]
=
[
z1
,
z2
]
return
samples
#目标分布p(z)
mus
=
np
.
array
([
3
,
3
])
sigmas
=
np
.
array
([[
1
,
.
7
],
[
.
7
,
1
]])
#确定总的采样期和燃烧期
burn_period
=
int
(
1e4
)
samples_period
=
int
(
1e5
)
#得到采样样本,舍弃燃烧期样本点
samples
=
gibbs_sampling
(
mus
,
sigmas
,
samples_period
)[
burn_period
:]
plt
.
plot
(
samples
[:,
0
],
samples
[:,
1
],
'ro'
,
alpha
=
0.05
,
markersize
=
1
)
plt
.
show
()
运行结果:
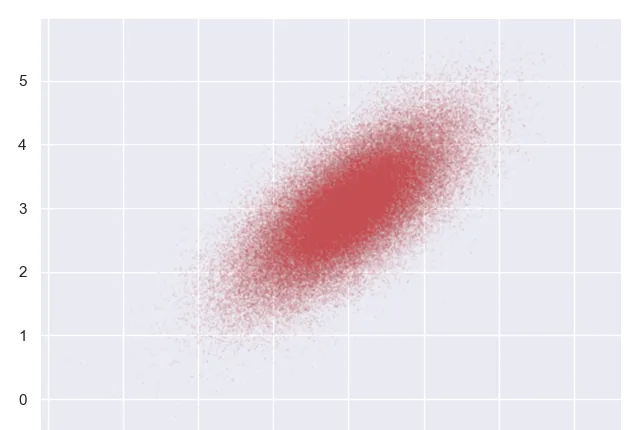
这个采样结果的分布,看上去是满意的,以上就是Gibbs采样的原理和演示过程。
此内容节选自我的专栏【机器学习中的数学:概率图与随机过程】,前三节可免费试读,欢迎订阅!
当然还有【机器学习中的数学(全集)】系列专栏,欢迎大家阅读,配合食用,效果更佳~
有订阅的问题可咨询微信:zhangyumeng0422











