先問是不是,再問為什麽。
球的體積公式 \frac43\pi r^3 ,對 r 求導確實可以得到球的表面積公式 4\pi r^2 。
但是 誰又規定了球的體積公式必須得用 r 作為自變量呢 ?考慮用直徑作為自變量的體積公式 \frac\pi6d^3 ——實際上在工程學語境下這個還要更常用一些,因為直徑比半徑好測量——對 d 求導得到的是 \frac\pi2d^2 ,而不是表面積 \pi d^2 。或者更過分一點,考慮用表面積作為自變量的體積公式 \frac{S^\frac32}{6\sqrt{\pi}} ,對 S 求導之後得到 \frac{\sqrt S}{4\sqrt\pi} ——更不知道跑哪兒去了。
可見,「體積求導等於表面積」成立與否,至少要取決於「體積公式中使用的是哪個量」,而不只是取決於「是什麽幾何體的體積」。
那麽球的半徑比起其他的量又有什麽特殊的呢?
要回答這個問題,不妨先看看導數的定義。不嚴格地來講,導數(導函式)的定義就是因變量隨自變量的增長率,或者說因變量「極微小變化」與自變量「極微小變化」的比值。那麽我們考慮一個球和與其同心的一個稍微大了一點的球,這裏的因變量——體積——的「極微小變化」就是多出來的那一層殼兒的體積。
這層殼兒的體積該怎麽算呢?我們想象這個殼兒是由很多很多稍稍彎曲的瓷磚拼接成的(可以想象一個球形的建築穹頂,天文台或者東方明珠電視塔那種的),不難發現每塊瓷磚的高度就是殼兒的厚度,而所有瓷磚的面積之和就是球的表面積。因為一個球只是比另一個球稍微大了一點,這個殼兒也是非常薄的,每塊稍稍彎曲的瓷磚就幾乎是一個沒有彎曲的柱體,所有柱體的底面積之和就是球的表面積,高則是殼兒的厚度。換句話來說,因變量的「極微小變化」和殼的厚度之比就是球的表面積了。而殼的厚度——不難發現——正是兩球的半徑之差,也就是半徑的「極微小變化」(而不是直徑的);因此,體積的「極微小變化」和半徑的「極微小變化」之比可以得到表面積。
總之,之所以只有對半徑求導才得到表面積,就是因為球和稍大的球之間那層「殼」的厚度正是半徑的差值。此外,題主也提到了對圓來說有類似的關系;分析一下不難發現,兩個同心圓之間「殼」的厚度也同樣是半徑的差值。
那麽對於其他的可以構造出「殼」的圖形,也有類似的關系嗎?
我們可以試試看。
比如正方形,大正方形和小正方形同心擺放,不難看出殼兒的厚度是「半邊長」的差值。設正方形的「半邊長」為 x ,則面積為 (2x)^2=4x^2 ;求導得到的 8x 也正是正方形的周長。
當然,兩個同心擺放的立方體也完全類似,會得到厚為「半棱長」差值的一層殼兒。設立方體的「半棱長」為 x ,則體積為 (2x)^3=8x^3 ;求導得到 24x^2=6\cdot(2x)^2 ,也正是立方體的表面積。
這樣聽起來,就有一個很誘人的結論擺在我們面前——
——橢圓和稍大的橢圓之間也是一層「殼兒」,那麽對橢圓的面積 \pi ab 求導,似乎就可以得到著名的無法簡單表示的 橢圓周長 了。比如,考慮離心率 \frac{c}{a}=0.6 的橢圓,就有 b=0.8a ,橢圓面積就是 0.8\pi a^2 ,周長是否就是 1.6\pi a 了呢?
這種好事自然是不存在的——相信有的讀者已經看出了個中原因:將兩個同樣離心率的橢圓同心重疊得到的「殼兒」厚度並不均勻,只有在長軸端點附近厚度才是 a 的差值,在短軸端點附近厚度就只有 b 的差值那麽厚了。
因此,前面的結論還需要改良一下: 若兩個體積相差很小的同種圖形/立體,其面積/體積之差可表示為一層 厚度均勻的 「殼兒」,且這個「殼兒」的厚度能表示為某個長度的差值,則面積/體積對這個長度的導數就是這種圖形/立體的周長/表面積。
這裏再舉一個例子。考慮下圖中的任意三角形 \triangle ABC 及與其相似的大一圈的三角形 \triangle A'B'C' :
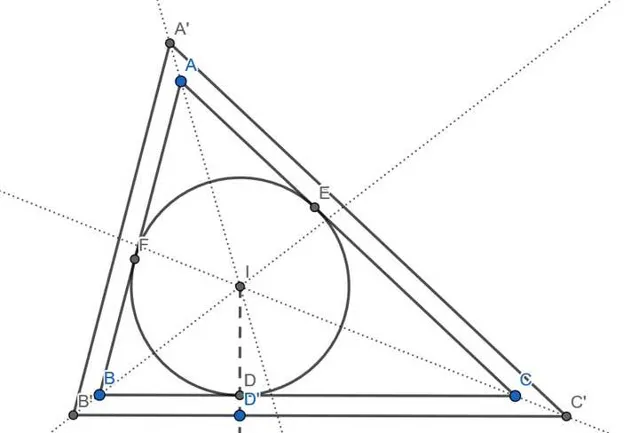
從圖中不難發現,三角形的內切圓半徑 r 正是我們要找的那個「差值等於‘殼兒’厚度」的長度。
那麽為了用 r 表示 \triangle ABC 的周長和面積,不妨設 \begin{cases} \angle BAC = 2\alpha \\ \angle ABC = 2\beta \\ \angle ACB = 2\gamma \end{cases} ,則有
\begin{align} S_{\triangle ABC}&=\frac12AB\cdot r+\frac12BC\cdot r+\frac12CA\cdot r\\ &=\frac r2\left(\frac r{\tan \alpha}+\frac r{\tan \beta}\right)+\frac r2\left(\frac r{\tan \beta}+\frac r{\tan \gamma}\right)+\frac r2\left(\frac r{\tan \gamma}+\frac r{\tan \alpha}\right)\\ &=r^2\left(\frac1{\tan \alpha}+\frac1{\tan \beta}+\frac1{\tan \gamma}\right) \end{align}
以及
\begin{align} C_{\triangle ABC}&=AB+BC+CA\\ &=\left(\frac r{\tan \alpha}+\frac r{\tan \beta}\right)+\left(\frac r{\tan \beta}+\frac r{\tan \gamma}\right)+\left(\frac r{\tan \gamma}+\frac r{\tan \alpha}\right)\\ &=2r\left(\frac1{\tan \alpha}+\frac1{\tan \beta}+\frac1{\tan \gamma}\right)\\ \end{align}
顯然前者對 r 求導即可得到後者。
再舉一個三維的例子。考慮棱長分別為 a,b,c 的長方體,給它增加一層厚度為 d 的殼兒之後棱長就會變成 a+2d,b+2d,c+2d 。由此可見, \frac a2,\frac b2,\frac c2 這三個量在變化前後的差值都等於殼兒的厚度。因此,不妨令 \frac a2=x ,再將 \frac b2,\frac c2 分別表示為 x+\frac{b-a}2,x+\frac{c-a}2 ,這樣三棱長就都以「差值等於殼兒厚度」的 x 表示出來了。(註意,由於 x 的增加量是殼兒的厚度,不可以將 \frac b2 表示為 x\cdot\frac ba ,否則 x 變化時棱長的變化量就和 x 的變化量不同,也就無法使用上面的原理了。此外,為了進一步表明 x 變化時 \frac{b-a}2,\frac{c-a}2 不應該隨之變化,也為了簡化推導步驟,下文設 y=b-a,z=c-a 。)
那麽,用這個表示法求一下長方體的體積和表面積:
\begin{align} V&=abc\\ &=2x(2x+y)(2x+z)\\ &=8x^3+4x^2(y+z)+2xyz \end{align}
\begin{align} S&=2ab+2bc+2ac\\ &=4x(2x+y)+2(2x+y)(2x+z)+4x(2x+z)\\ &=(8x^2+4xy)+(8x^2+4x(y+z)+2yz)+(8x^2+4xz)\\ &=24x^2+8x(y+z)+2yz \end{align}
不難看出體積對 x 求導仍能得出表面積。
至此,「均勻殼兒差原理」(暫定名)應該可以說相當牢靠了。球的表面積也只是這個原理的一個例項。
嗯,這很好,那麽這嚴謹嗎?數學嗎?
——突然想自辯兩句了。
其實我在知乎上回答偏數學的問題的時候,一般都絕不會把嚴謹性放在首位,而是把「建立思路」或者「建立正確的直覺」放在首位。我個人在看其他回答的時候也更喜歡那些有助於建立正確的直覺而不只是shut up and calculate的,若是看到一句解釋也沒有的純計算回答(這樣的回答還挺不少的),更是容易一口氣捯不上來。不是說寫積分式不好,但寫了積分式卻不說為什麽積分式能解決問題,在我看來很可能實在幫不上這些問題的題主(否則題主為什麽不直接問某個積分怎麽算呢?)。
但「論證的時候只提直觀不提嚴謹性」不代表「論證無法嚴謹化/公理化/形式化」。就說說這次的這個「均勻殼兒差原理」吧—— 若兩個體積相差很小的同種圖形/立體,其面積/體積之差可表示為一層 厚度均勻的 「殼兒」,且這個「殼兒」的厚度能表示為某個長度的差值,則面積/體積對這個長度的導數就是這種圖形/立體的周長/表面積。
接下來,把這段話變成「數學語」。
(高中同學請註意:
如果這裏的「函式」是電勢的相反數 -U ,那麽某點處「函式的梯度」就是電場強度 E ,大小與 U 下降的「速度」成正比,方向沿著 U 下降的方向,即 -U 上升的方向;
如果這裏的「函式」是高度 h ,那麽某點處「函式的梯度」大小是這一點最陡的坡度(即傾角的正切 i=\tan\theta ),方向是沿著最陡的坡向上。
簡而言之,梯度就是一個方向沿著變化最快的方向向上、大小與變化率相同的東西。)
而「厚度均勻」這個條件,想想看「等高線均勻」意味著什麽也就容易明白了—— 各點的梯度大小相同 。
那麽萬事俱備,「均勻殼兒差原理」終於可以變成「數學語」了: 對於梯度大小恒定的函式 f ,有 \frac{\mathrm d\left(\int_{f\leqslant r}\mathrm dV\right)}{\mathrm d\frac{r}{|\nabla f|}}=\int_{f=r}\mathrm dA 。 這其實就是更具一般性的 余面積公式 (coarea formula)的一個特殊形式——其他答主也指出了這一點。(若對不均勻的殼兒考慮「體積的微小變化量等於殼兒厚度在整個表面上的積分」,透過這個思路甚至可以匯出余面積公式的一般形式;不過此處暫且按下不表。)










